一、y″=f(x)型如属此类型,只要积分两次就可得出通解,可由初始条件确定这两个任意常数而得到特解.一般地,对n阶方程y(n)=f(x),积分n次便可得到通解二、y″=f(x,y′)型特点:方程右端不明显地含未知函数y.令y′=p(x),则y″=p′(x)代入原方程得p′(x)=f(x,p(x)),它是关于未知函数p(x)的一阶微分方程.这种方法叫做降阶法.解此一阶方程可求出其通解p=p(x,C1......
2023-11-22
【主要内容】
二阶微分方程的一般形式是F(x,y,y′,y″)=0(其中y″必定出现),它的标准形是y″=f(x,y,y′).
有三类二阶微分方程可降阶成一阶微分方程,然后求解,分别如下:
1.微分方程y″=f(x).
求这类微分方程通解的步骤如下:
(1)降阶成一阶微分方程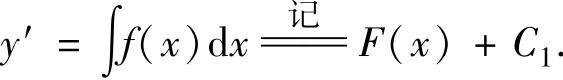
(2)于是二阶微分方程的通解为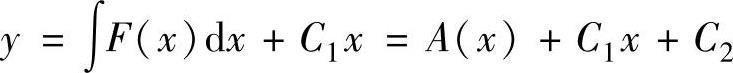 (其中,
(其中,
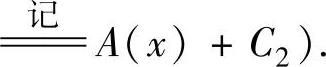
2.微分方程y″=f(x,y′)
求这类微分方程通解的步骤如下:
(1)令p=y′降阶为一阶微分方程p′=f(x,p),设它的通解为p=φ(x,C1),即
(2)求解式(∗)得二阶微分方程的通解为
3.微分方程y″=f(y,y′)
求这类微分方程通解的步骤如下:
(1)令p=y′降阶成一阶微分方程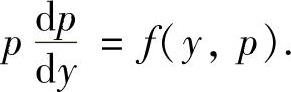 设它的通解为p=φ(y,C1),即
设它的通解为p=φ(y,C1),即
(2)求解式(∗∗)得二阶微分方程的通解
【典型例题】
例4.3.1 求微分方程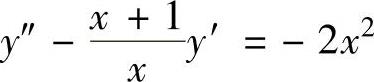 的通解.
的通解.
精解 所给微分方程是y″=f(x,y′)类型的二阶微分方程,所以令p=y′,则所给微分方程降阶为
式(1)的通解
由此得到
因此,原微分方程的通解为
例4.3.2 求微分方程xy″+x(y′)2-y′=0满足 的特解.
的特解.
精解 所给微分方程是y″=f(x,y′)类型的二阶微分方程,所以令p=y′,则所给微分方程降阶成 ,即
,即 (n=2的伯努利方程).(1)
(n=2的伯努利方程).(1)
令z=p1-2=p-1,则(1)成为
它的通解为(www.chuimin.cn)
由初始条件 得zx=2=2,将它代入式(2)得
得zx=2=2,将它代入式(2)得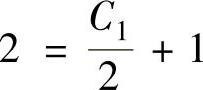 ,即C1=2.所以
,即C1=2.所以 ,即
,即
由此得到
从而原微分方程的通解为
将初始条件y(2)=0代入式(3)得0=ln8+C2,即C2=-3ln2.所以所求微分方程的
特解为
y=ln(4+x2)-3ln2.
例4.3.3 求微分方程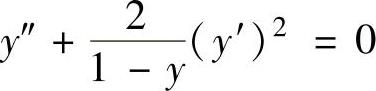 的通解.
的通解.
精解 所给微分方程是y″=f(y,y′)类型的二阶微分方程,令p=y′,则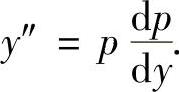 将
将
它们代入所给的微分方程得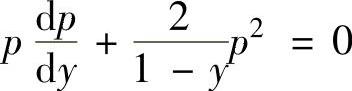 ,
,
即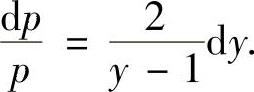
上式两边分别积分得
lnp=2ln(y-1)+lnC1,即p=C1(y-1)2.由此得到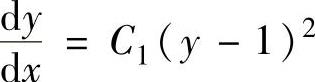 ,即
,即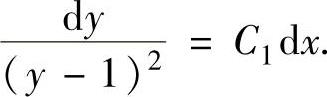 上式两边分别积分得原微分方程的通解为
上式两边分别积分得原微分方程的通解为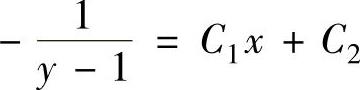 ,即
,即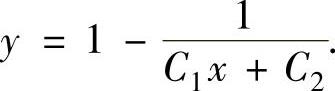
例4.3.4 求微分方程y″+(y′)2=1满足y(0)=y′(0)=0的特解.
精解 所给的微分方程是y″=f(y,y′)类型的二阶微分方程,令p=y′则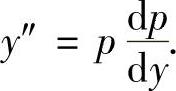 将
将
它们代入所给的微分方程得 ,即
,即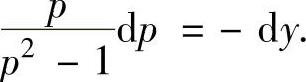
上式两边分别积分得 ,即p2=C1e2y+1.(1)
,即p2=C1e2y+1.(1)
将y(0)=0,p(0)=y′(0)=0代入式(1)得C1=-1.于是式(1)成为p2=1-e-2y,即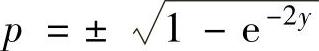 .
.
由此得到 ,即
,即
上式两边分别积分得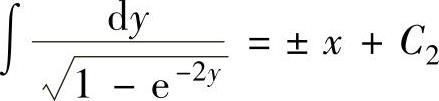 ,即
,即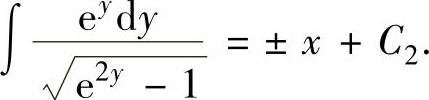
所以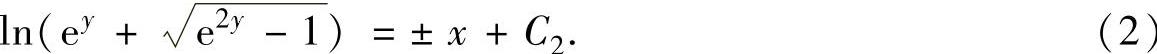
将y(0)=0代入式(2)得C2=0.所以 ,
,
即 ,得
,得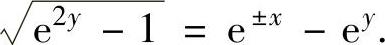
上式两边平方得e2y-1=e±2x-2e±xey+e2y,即
因此所求的特解为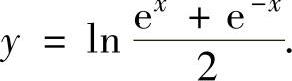
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

一、y″=f(x)型如属此类型,只要积分两次就可得出通解,可由初始条件确定这两个任意常数而得到特解.一般地,对n阶方程y(n)=f(x),积分n次便可得到通解二、y″=f(x,y′)型特点:方程右端不明显地含未知函数y.令y′=p(x),则y″=p′(x)代入原方程得p′(x)=f(x,p(x)),它是关于未知函数p(x)的一阶微分方程.这种方法叫做降阶法.解此一阶方程可求出其通解p=p(x,C1......
2023-11-22

一、二阶常系数非齐次线性方程解的结构定理5若y*是二阶常系数线性非齐次方程的一个特解,Y=c1y1+c2y2是方程(1)对应的二阶常系数线性齐次方程的通解,则是方程(1)的通解.二、二阶常系数非齐次线性方程的解法下面我们根据f(x)具有下列特殊情形时,来给出求其特解的公式:【例题1】求方程y″+4y′+3y=x-2的一个特解.解:对应的特征方程为p2+4p+3=0.原方程右端不出现eμx,但可......
2023-11-20

【主要内容】形如y″+py′+qy=f(x)()(其中p,q是常数,f(x)是已知函数,且不恒为零)的微分方程,称为二阶常系数非齐次线性微分方程,称y″+py′+qy=0()是式()对应的齐次线性微分方程.如果Y(x)是式()的通解,y(x)是式()的一个特解,则y(x)=Y(x)+y(x)是式()的通解.关于二阶常系数非齐次线性微分方程()的特解有以下结论:(1)当f(x)=Pm(x)eλx(其......
2023-10-27

回答是否定的,因为根据通解的定义,只有当c1,c2这两个常数相互独立时才是的通解.y1,y2在满足什么样的条件下,才能使得c1,c2相互独立呢?......
2023-11-20

【主要内容】形如y″+py′+qy=0 (其中,p,q是常数)()的微分方程,称为二阶常系数齐次线性微分方程.如果y1(x),y2(x)是式()的两个线性无关的特解,则y=C1y1(x)+C2y2(x)是式()的通解.称r2+pr+q=0为式()的特征方程.关于式()的通解有以下结论:(1)如果特征方程有两个不等的实根r1,r2,则式()的通解为(2)如果特征方程有两个相等的实根r1,r2(r1=......
2023-10-27

二阶齐次线性方程的解具有下列性质:定理1 如果函数y1与y2是方程的两个解,那么也是方程的解,其中C1、C2是任意常数.齐次线性方程的这个性质表明它的解符合叠加原理.函数的线性相关与线性无关:定义1 设y1,y2,…......
2023-10-19
相关推荐