一、建立微分方程的数学模型解:设曲线方程为y=f(x),且曲线上任意一点的坐标为(x,y).根据题意以及导数的几何意义可得两边同时求不定积分得y=∫xdx,这就是所求的曲线方程.引例2求方程y"=cosx的通解.解:一次积分得:二次积分即得到方程的通解:以上我们仅以物理学、几何学引出关于变量之间微分方程的关系,其实在化学、生物学、自动控制、电子技术等学科中都提出了许多有关微分方程的问题,从而要......
2023-11-20
【主要内容】
1.微分方程的概念
含有自变量x,未知函数y及其导数(其中未知函数的导数必出现)的方程称为常微分方程(简称微分方程),其中,未知函数导数的最高阶数称为该微分方程的阶.
如果将函数y=φ(x)代入微分方程后成为恒等式,则称y=φ(x)是该微分方程的解;如果由Φ(x,y)=0确定的隐函数y=φ(x)是微分方程的解,则称Φ(x,y)=0是该微分方程的隐解.如果函数y=φ(x,C1,C2,…,Cn)(其中,C1,C2,…,Cn是n个独立的任意常数)是n阶微分方程的解,则称其为该n阶微分方程的通解.如果由初始条件确定了y=φ(x,C1,C2,…,Cn)中的C1,C2,…,Cn的值,则称其为该微分方程的特解.
一阶微分方程的一般形式是F(x,y,y′)=0(其中y′必定出现),标准形是y′=f(x,y).一阶微分方程是指变量可分离微分方程、齐次微分方程、一阶线性微分方程(包括伯努利方程).
2.变量可分离微分方程形如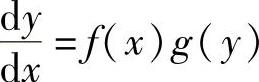 (其中,f(x),g(y)是已知函数)的微分方程称为变量可分离微分方
(其中,f(x),g(y)是已知函数)的微分方程称为变量可分离微分方
程,它的通解为
3.齐次微分方程
形如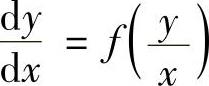 (其中f(u)是已知函数)的微分方程称为齐次微分方程.
(其中f(u)是已知函数)的微分方程称为齐次微分方程.
令 ,则原微分方程成为
,则原微分方程成为 ,它是以u为未知函数的变量可分离微分方程.
,它是以u为未知函数的变量可分离微分方程.
【典型例题】
例4.1.1 (单项选择题)微分方程y′sinx=ylny满足条件 的特解为( ).
的特解为( ).
A.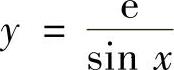 B.y=esinxC.
B.y=esinxC.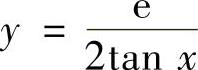 D.
D.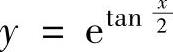
精解 容易验证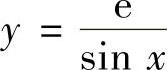 ,y=esinx都不满足所给微分方程,所以A,B两个选项都不能
,y=esinx都不满足所给微分方程,所以A,B两个选项都不能
选,另外, 在点
在点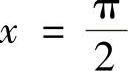 处没有定义,所以也不能选C.
处没有定义,所以也不能选C.
因此本题选D.(www.chuimin.cn)
例4.1.2 求微分方程(ex+y-ex)dx+(ex+y+ey)dy=0的通解.
精解 所给微分方程可以改写成ey(ex+1)dy=-ex(ey-1)dx (变量可分离微分方程)
即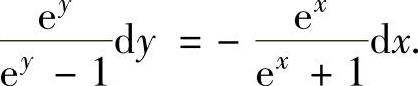
上式两边分别积分得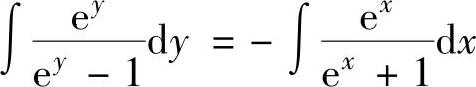 ,即ln(ey-1)=-ln(ex+1)+lnC,
,即ln(ey-1)=-ln(ex+1)+lnC,
所以所给微分方程的通解为(ex+1)(ey-1)=C.
例4.1.3 求微分方程(lnx-lny-1)ydx+xdy=0的通解.
精解 所给微分方程可以改写为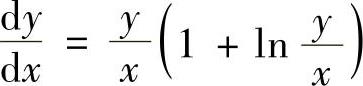 (齐次微分方程)(1)令
(齐次微分方程)(1)令 ,则式(1)成为
,则式(1)成为 ,即
,即 (变量可分离微分方程).
(变量可分离微分方程).
它的通解为ln(lnu)=lnx+lnC,即u=eCx,从而原微分方程的通解为y=xeCx.
例4.1.4 求微分方程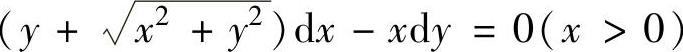 的满足初始条件yx=1=0的特解.
的满足初始条件yx=1=0的特解.
精解 先算出所给微分方程的通解,再由初始条件确定通解中任意常数的值.
所给微分方程可以改写成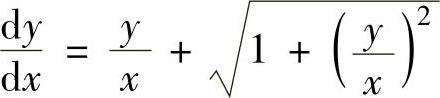 (齐次微分方程)(1)
(齐次微分方程)(1)
令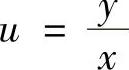 ,则式(1)成为
,则式(1)成为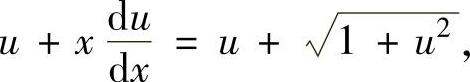 即
即 (变量可分离微分方程).
(变量可分离微分方程).
它的通解为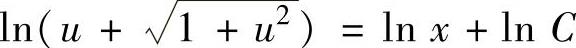 ,即
,即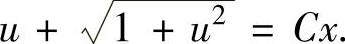 于是原微分方程的通解为
于是原微分方程的通解为
由初始条件yx=1=0得式(2)中的C=1.所以所给微分方程满足初始条件yx=1=0的特解为 ,即
,即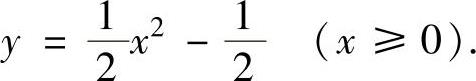
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

一、建立微分方程的数学模型解:设曲线方程为y=f(x),且曲线上任意一点的坐标为(x,y).根据题意以及导数的几何意义可得两边同时求不定积分得y=∫xdx,这就是所求的曲线方程.引例2求方程y"=cosx的通解.解:一次积分得:二次积分即得到方程的通解:以上我们仅以物理学、几何学引出关于变量之间微分方程的关系,其实在化学、生物学、自动控制、电子技术等学科中都提出了许多有关微分方程的问题,从而要......
2023-11-20

知识要点1.微分方程的基本概念:微分方程的定义、阶、通解、特解.2.可分离变量的微分方程:求解可分离变量微分方程的步骤:(1)分离变量;(2)两端分别积分,可得原方程的通解.如果问题为求特解,只需将初始条件代入求得的通解,确定常数C的值即可.3.一阶线性非齐次微分方程:形式:y′+P(x)y=Q(x).求解方法有以下两种:(1)常数变易法:第一步,先求对应的齐次微分方程y′+P(x)y=0的通解......
2023-10-26

一、二阶常系数非齐次线性方程解的结构定理5若y*是二阶常系数线性非齐次方程的一个特解,Y=c1y1+c2y2是方程(1)对应的二阶常系数线性齐次方程的通解,则是方程(1)的通解.二、二阶常系数非齐次线性方程的解法下面我们根据f(x)具有下列特殊情形时,来给出求其特解的公式:【例题1】求方程y″+4y′+3y=x-2的一个特解.解:对应的特征方程为p2+4p+3=0.原方程右端不出现eμx,但可......
2023-11-20

首先研究最简单的一阶微分方程,即可分离变量的微分方程.一、可分离变量的方程可以化成形如形式的方程称为可分离变量的微分方程.对M(x)dx=N(y)dy两端分别积分,便得方程的通解:∫M(x)dx=∫N(y)dy+C(C是任意常数).例1 求方程(1+y2)dx-x(1+x2)ydy=0的通解.解 用x(1+x2)(1+y2)除方程两边整理得两边积分因为,,所以即,或,通解为(1+x2)(1+y2)......
2023-11-22

一般地,形如的一阶微分方程称为可分离变量的一阶微分方程.当g(y)≠0时,方程(7.2.1)可写为这样一来,变量y与x便被分离在等号的两端了.设f(x)与g(x)都连续,求解方程(7.2.1),就是要寻找函数y=y(x),将它代入方程(7.2.1)后,能使此方程成为恒等式.从而,当g(y)≠0时,就有在解微分方程时,为了突出任意常数C,常把中所含的任意常数C明确写出来.根据不定积分的第一换元法,得......
2023-10-19

【主要内容】形如y″+py′+qy=f(x)()(其中p,q是常数,f(x)是已知函数,且不恒为零)的微分方程,称为二阶常系数非齐次线性微分方程,称y″+py′+qy=0()是式()对应的齐次线性微分方程.如果Y(x)是式()的通解,y(x)是式()的一个特解,则y(x)=Y(x)+y(x)是式()的通解.关于二阶常系数非齐次线性微分方程()的特解有以下结论:(1)当f(x)=Pm(x)eλx(其......
2023-10-27

回答是否定的,因为根据通解的定义,只有当c1,c2这两个常数相互独立时才是的通解.y1,y2在满足什么样的条件下,才能使得c1,c2相互独立呢?......
2023-11-20
相关推荐