首页理论教育二次积分次序或坐标系更换方法

二次积分次序或坐标系更换方法

2023-10-27 理论教育版权反馈

【摘要】：【主要内容】1.二次积分积分次序的更换方法设f（x，y）是连续函数，则要更换二次积分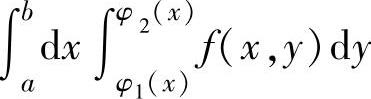的积分次序，即将“先y后x”的积分次序更换成“先x后y”的积分次序，可按以下步骤进行：（1）确定对应的二重积分的积分区域D={（x，y）|a≤x≤b，φ1（x）≤y≤φ2（x）}，并画出D的图形；（2）由D的图形，将D改写成D={（x，y）|c≤y≤d，ψ1（y）≤x≤ψ2（y）}，由此得到与所给二次积分相等、但次

【主要内容】

1.二次积分积分次序的更换方法

设f（x，y）是连续函数，则要更换二次积分的积分次序，即将“先y

后x”的积分次序更换成“先x后y”的积分次序，可按以下步骤进行：

（1）确定对应的二重积分的积分区域

D={（x，y）|a≤x≤b，φ₁（x）≤y≤φ₂（x）}，并画出D的图形；

（2）由D的图形，将D改写成

D={（x，y）|c≤y≤d，ψ₁（y）≤x≤ψ₂（y）}，

由此得到与所给二次积分相等、但次序为“先x后y”的二次积分

同样，也可以由“先x后y”的二次积分更换成“先y后x”的二次积分.

2.坐标系的更换

设f（x，y）是连续函数，则要把直角坐标系中的二次积分或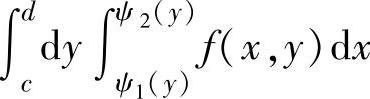更换成极坐标系中的二次积分∫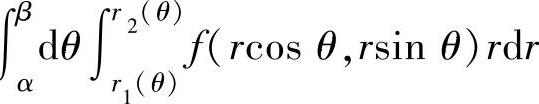，可按以下步

骤进行：

（1）确定或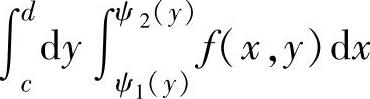的二重积分的积分区域

D={（x，y）|a≤x≤b，φ₁（x）≤y≤φ₂（x）}

或D={（x，y）|c≤y≤d，ψ₁（y）≤x≤ψ₂（y）}，并画出D的图形；

（2）由D的图形，将D改写成

D={（r，θ）|α≤θ≤β，r₁（θ）≤r≤r₂（θ）}，

由此得到与所给二次积分相等的极坐标系中的二次积分

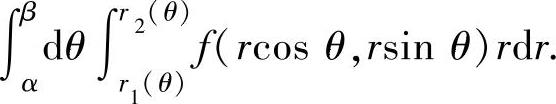
同样，也可以将极坐标系中的二次积分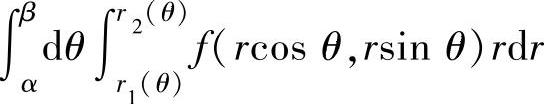更换成直角坐标系

中的二次积分.

【典型例题】

例3.9.1 设f（x，y）是二元连续函数，更换二次积分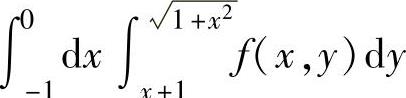的积分次序.

精解由所给的二次积分可知其对应的二重积分的积分区域为

D={（x，y）|-1≤x≤0，，

D如图3.9.1的阴影部分所示.

由图可知，要将D的表达式改写成

D={（x，y）|c≤y≤d，

ψ₁（y）≤x≤ψ₂（y）}，需用水平直线y=1将D划分成D₁，D₂（见图3.9.1），即D=D₁+D₂，其中(www.chuimin.cn)

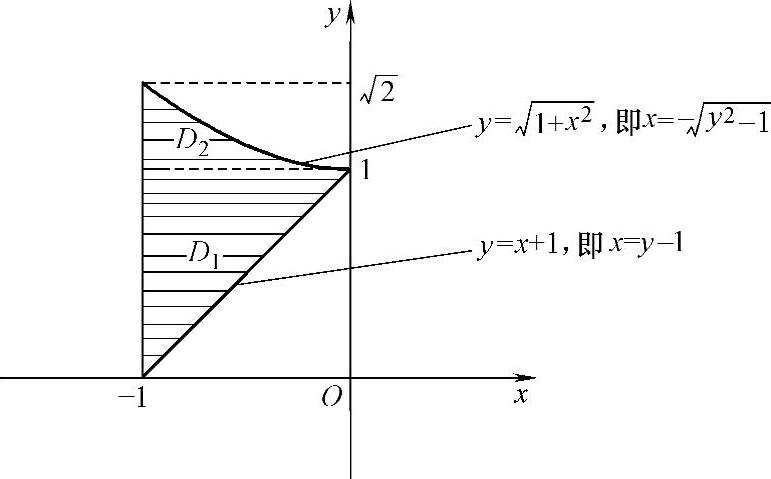
图 3.9.1

D₁={（x，y）|0≤y<1，-1≤x≤y-1}，，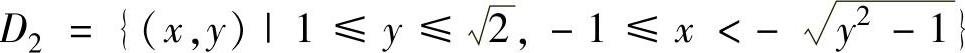

于是有

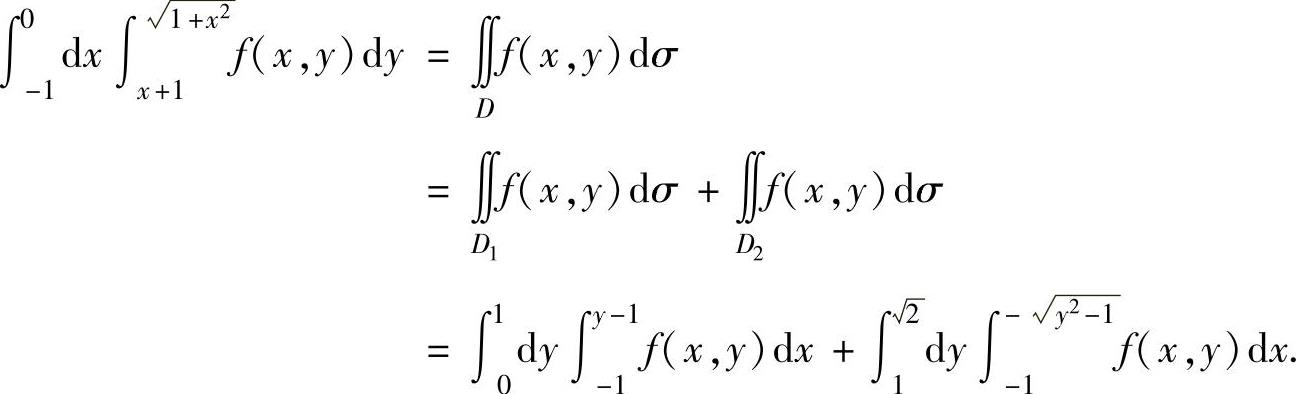
例3.9.2 计算二次积分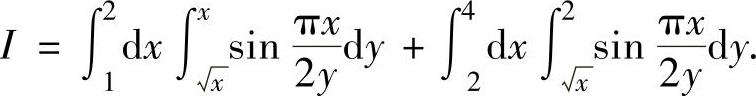

精解由于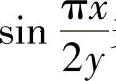关于y的原函数不能算出，即所给的两个二次积分不能直接计算，所

以先更换二次积分的积分次序然后再进行计算.

由于，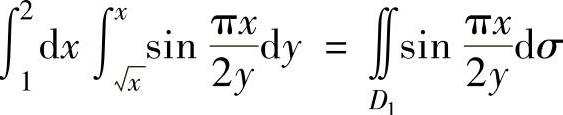

其中；，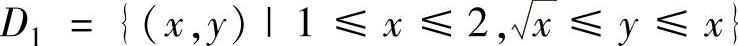

其中，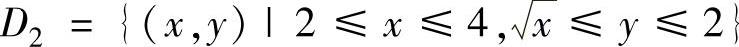

并且D₁，D₂如图3.9.2阴影部分所示.所以由图可知，D=D₁+D₂={（x，y）|1≤y≤2，y≤x≤y²}.

于是

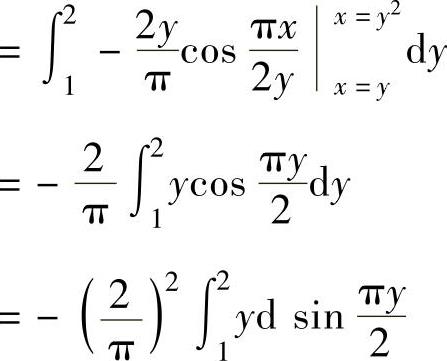
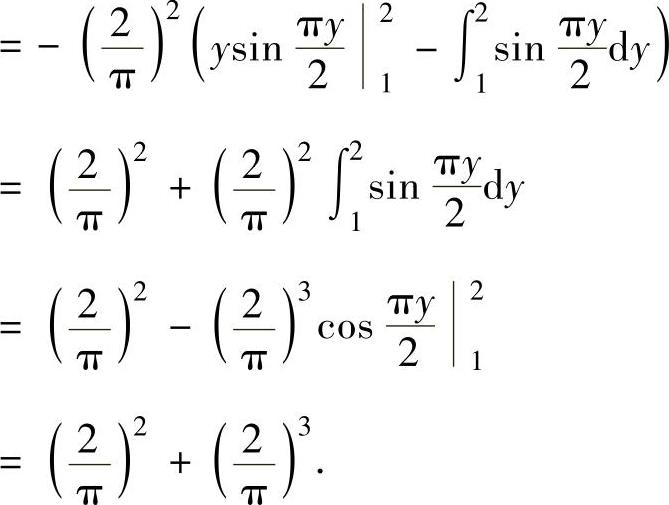
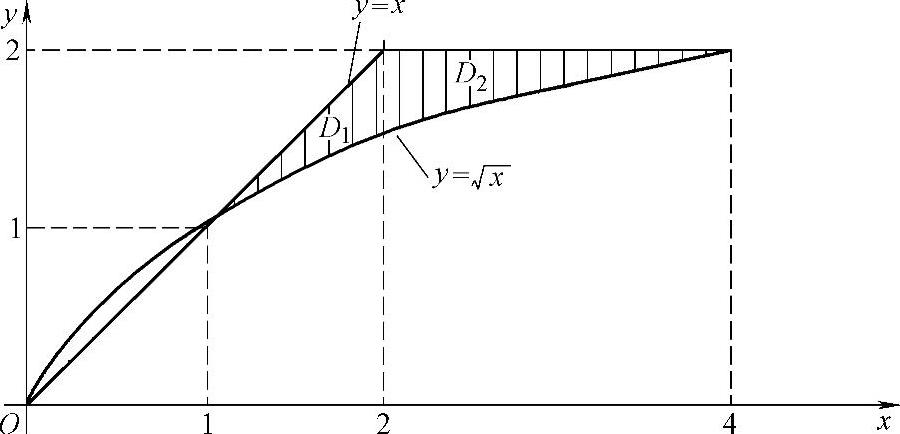
图 3.9.2

例3.9.3 求极限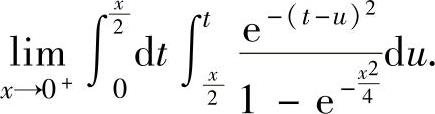

精解

是型未定式极限，为了应用洛必达法则，必须将分子的二次积分中的x移到外层积分上限，故需更换积分次序

将式（2）代入式（1）得

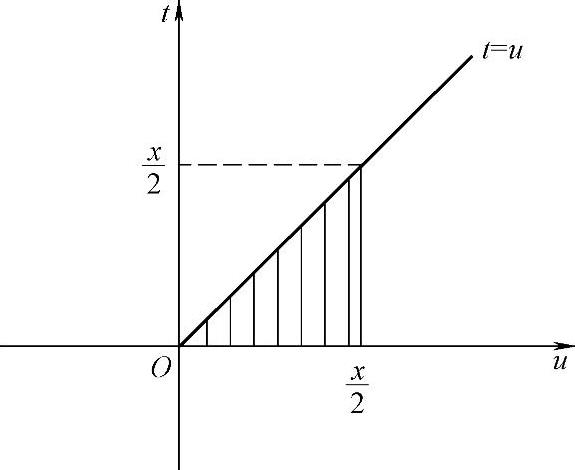
图 3.9.3

例3.9.4 设f（x，y）是连续函数，求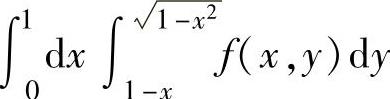在极坐标系下的二次积分（先r后θ）.

精解，其中积分区域D={（x，y）|0≤x≤1，，

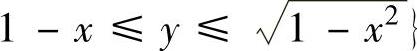如图3.9.4阴影部分所示，它的极坐标系下可表示为，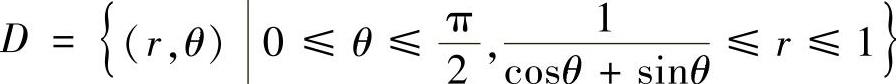

所以，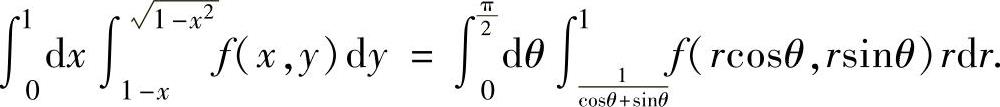

图 3.9.4