1.设函数f在[a,b]上连续,则f在[a,b]上必有最大值M与最小值m.它们可按以下步骤计算:算出f在(a,b)内的所有可能极值点,记为x1,x2,…......
2023-10-27
【主要内容】
1.二元情形
设二元函数f(x,y)在有界闭区域D上连续,则它在D上必能取到最大值与最小值,当f(x,y)还在D的内部可微时,则最大值与最小值可按以下步骤计算:
(1)计算f(x,y)在D的内部的所有可能极值点,记为(x1,y1),(x2,y2),…,(xn,yn).
(2)计算f(x,y)在D的边界上的最大值与最小值,分别记为M1,m1,其中M1,m1可以把边界方程代入f(x,y)转化成一元函数最值问题计算,也可以把边界方程作约束条件,用拉格朗日乘数法计算.
(3)比较f(x1,y1),f(x2,y2),…,f(xn,yn),M1,m1,其中最大者即为f(x,y)在D上的最大值,最小者即为f(x,y)在D上的最小值.
2.三元情形
设三元函数f(x,y,z)在有界闭区域Ω上连续,则它在Ω上必能取到最大值与最小值,当f(x,y,z)在Ω内部可微时,其最大值与最小值的计算方法与二元情形相同.
【典型例题】
例3.7.1求二元函数f(x,y)=x2+2y2-x2y2在闭区域D={(x,y)|x2+y2≤4,y≥0}上的最大值与最小值.
精解 先计算f(x,y)在D内部{(x,y)|x2+y2<4,y>0}的所有可能极值点.
解方程组 即
即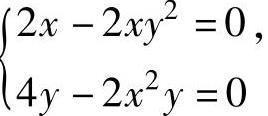 得
得 ,y=1,所以f(x,y)在D的内部的所有
,y=1,所以f(x,y)在D的内部的所有
可能极值点为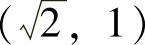 ,
,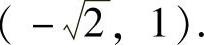
下面计算f(x,y)在D的边界C上的最值.边界C由C1:x2+y2=4(-2≤x≤2,y≥0)和C2:y=0(-2≤x≤2)组成.在C1上,f(x,y)=x2+2(4-x2)-x2(4-x2)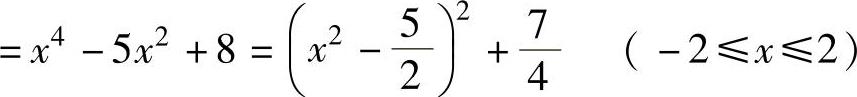 ,
,
所以f(x,y)在C1上的最大值为8(即 在x=0处的值),最小值为
在x=0处的值),最小值为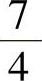
 在
在
在C2上,f(x,y)=x2(-2≤x≤2),所以f(x,y)在C2上的最大值为4,最小值为0.
由此可知,f(x,y)在C上的最大值为8,最小值为0.
由于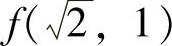 ,
,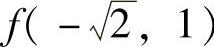 ,8,0,即2,2,8,0中最大者为8,最小者为0,所以,
,8,0,即2,2,8,0中最大者为8,最小者为0,所以,
f(x,y)在D上的最大值为8,最小值为0.
例3.7.2 求二元函数f(x,y)=3x2+3y2-x3在有界闭区域D={(x+y)|x+y≤1,x≥0,y≥0}上的最大值与最小值.
精解 先计算f(x,y)在D内部{(x,y)|x+y<1,x>0,y>0}的可能极值点.解方程组 即{
即{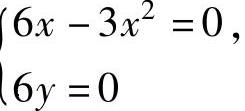 得x=0,y=0;x=2,y=0,故f(x,y)的可能极值点为(0,0)和(2,0).显然它们都不在D的内部,即在D的内部f(x,y)无可能极值点.
得x=0,y=0;x=2,y=0,故f(x,y)的可能极值点为(0,0)和(2,0).显然它们都不在D的内部,即在D的内部f(x,y)无可能极值点.
下面计算f(x,y)在D的边界C上的最值,显然它的最大值、最小值即为f(x,y)在D上的最大值、最小值.
边界C由三部分组成,即Ⅰ:x+y=1(0≤x≤1);Ⅱ:y=0(0≤x≤1);Ⅲ:x=0(0≤y≤1).
在Ⅰ上,y=1-x,所以
由于φ′(x)=-6+12x-3x2=-3(x2-4x+2)在(0,1)内有唯一实根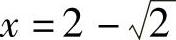 ,所以φ(x)
,所以φ(x)
在[0,1]上的最大值为max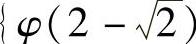 ,
,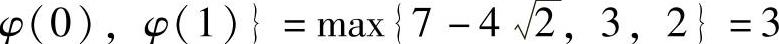 ,最小值
,最小值
为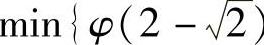 ,φ(0),
,φ(0),
在Ⅱ上,y=0,所以(www.chuimin.cn)
由于φ1′(x)=6x-3x2=3x(2-x)>0(0<x<1),所以φ1(x)在[0,1]上的最大值为φ1(1)=2,最小值为φ1(0)=0.
在Ⅲ上,x=0,所以
显然,φ2(y)在[0,1]上的最大值为φ2(1)=3,最小值为φ2(0)=0.
综上所述,f(x,y)在C上的最大值为max{3,2,3}=3,最小值为 ,
,
0}=0.从而f(x,y)在D上的最大值为3,最小值为0.
例3.7.3 求二元函数f(x,y)=x2+y2在闭区域
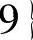 上的最大值与最小值.
上的最大值与最小值.
精解 先计算f(x,y)在D的内部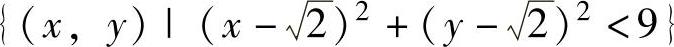 的极值点.
的极值点.
解方程组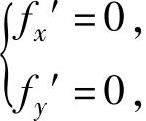 即
即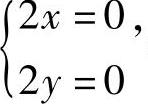 得x=y=0,所以f(x,y)在D的内部有唯一的可能极值点
得x=y=0,所以f(x,y)在D的内部有唯一的可能极值点
(0,0).下面计算f(x,y)在D的边界C: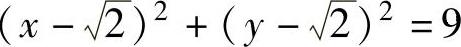 上的最值,应用拉格朗日乘
上的最值,应用拉格朗日乘
数法:记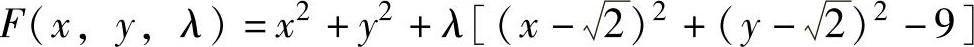 ,则
,则
于是方程组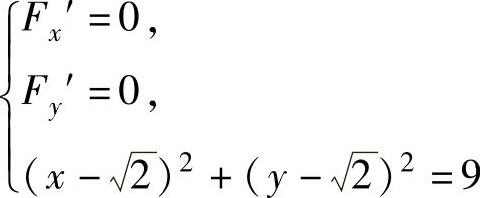
即为
由式(1)和式(2)知x=y,将它代入式(3)得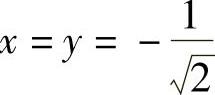 ,
,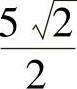 ,即f(x,y)在C上有两个可
,即f(x,y)在C上有两个可
能极值点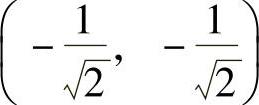 ,
,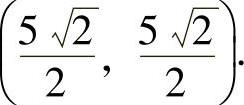 由于
由于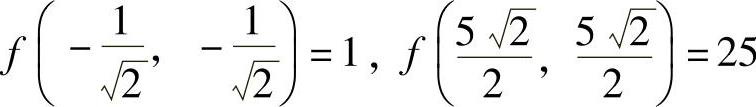 ,
,
所以,f(x,y)在C上的最大值为25,最小值为1.从而f(x,y)在D上的
最大值=max{f(0,0),25}=max{0,25}=25,
最小值=min{f(0,0),1}=min{0,1}=0.
例3.7.4 求三元函数u=x2+2y2+3z2在闭区域Ω={(x,y,z)|x2+y2+z2≤100}上的最值.
精解 先计算u在Ω内部{(x,y,z)|x2+y2+z2<100}的所有可能极值点.
解方程组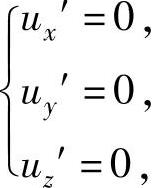 即
即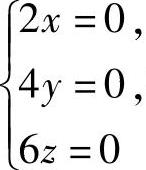 得x=y=z=0,所以u在Ω内部有唯一的可能极值点(0,0,0).
得x=y=z=0,所以u在Ω内部有唯一的可能极值点(0,0,0).
下面应用拉格朗日乘数法计算u在Ω的边界S:x2+y2+z2=100上的最值.
由于在S上u=x2+2y2+3z2=100+y2+2z2,所以,u在S上的最大值与最小值即为φ(y,z)=100+y2+2z2在yOz平面上闭区域D={(x,y)|y2+z2≤100}上的最大值与最小值.
先计算φ(y,z)在D的内部{(y,z)|y2+z2<100}的所有可能极值点.
解方程组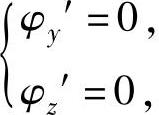 即
即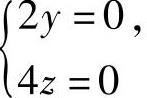 得y=z=0,所以φ(y,z)在D内部有唯一可能的极值点(0,0).
得y=z=0,所以φ(y,z)在D内部有唯一可能的极值点(0,0).
再计算φ(y,z)在D的边界C:y2+z2=100上的最值.
在C上,φ(y,z)=100+(y2+z2)+z2=200+z2(-10≤z≤10),显然它的最大值为300,最小值为200.
因此,φ(y,z)在D上的最大值=max{φ(0,0),300}=max{100,300}=300,最小值=min{100,200}=100.从而u在Ω上的最大值与最小值分别为300与0.
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

1.设函数f在[a,b]上连续,则f在[a,b]上必有最大值M与最小值m.它们可按以下步骤计算:算出f在(a,b)内的所有可能极值点,记为x1,x2,…......
2023-10-27

解 设AD=x,那么DB=100-x,由于铁路上每千米货运的运费与公路上每公里货运的运费之比为3∶5,因此不妨设铁路上每公里的运费为3k,公路上每公里的运费为5k.图3-10设从B点到C点需要的总运费为y,那么y=5k·CD+3k·DB,即得目标函数.现在来求x在区间[0,100]上取何值时,函数y的值最小.求导数:.令y′=0,得x=15.由于,,其中,以yx=15=380k为最小,因此当AD=15km时,总运费最省.......
2023-11-22

但在吊车梁按正常使用极限状态设计时,可采用吊车荷载的准永久值。排架柱A在支承吊车梁的牛腿部位由两台吊车运行至相近位置时,则可算得牛腿面上由吊车最大轮压产生的最大竖向反力标准值Rmax=____kN。计算时考虑两台吊车且每一车轮上均作用横向水平荷载h,相应地按1.3.2节的规定,取用多台(两台)吊车的水平荷载标准值折减系数0.9。......
2023-08-28

定义 设函数z=f(x,y)在点(x0,y0)的某个邻域内有定义,对于该邻域内异于点(x0,y0)的点(x,y):(1)若f(x,y)<f(x0,y0),则称函数在点(x0,y0)有极大值f(x0,y0);(2)若f(x,y)>f(x0,y0),则称函数在点(x0,y0)有极小值f(x0,y0).极大值、极小值统称为极值.使函数取得极值的点称为极值点.例1 函数z=3x2+4y2在点(0,0)处有......
2023-10-19

解:要使材料最省,就是要罐头筒的总表面积最小.设罐头的底半径为r,高为h,如图3.5所示,则它的侧面积为2πrh,底面积为πr2,因此总表面积为图3.5于是得出结论:当所做罐头筒的高和底直径相等时,所用材料最省.习题3.21.求函数的单调区间和极值.f=x2-2x+4;f=x2-6x;y=2x3-3x2;y=x-ln(1+x);f=x3-12x.2.运用极值的第二定理求极值.f=x2-2x;f=x4-2x2.3.求函数的最值.f=x2-2x+1,x∈[-1,2];f=x2-2x,x∈[0,2];f=x3-3x,x∈[0,2];f=x4-2x2,x∈[0,2].4.已知x+y=s,运用极值第二定理证明......
2023-11-20

我国对含零值系列频率分析的研究,先后提出了间接法、中值适线法以及Ⅱ型乘法分布等方法。配线的初估值,对于确定的b,可以直接根据频率曲线由下式估计:据此对频率曲线进行拟合,得最终确定的a、c值。......
2023-08-23

TM2、TM3共用一条进线进入GIS,TM4、TM5共用一条进线进入GIS。GIS一条出线预留,另两条出线经架空线与上下游电站连接。若要计算VFTO幅值极限值,则需考虑燃弧最严重的极端情形,即电源侧电压为峰值,母线残余电荷电压为电源电压反极性峰值的情况,此时隔离开关电源侧电压为1.0pu,负载侧电压为-1.0pu。频谱分析过程中将VFTO的直流分量过滤掉,得到不同频率下交流分量的幅值。GIS内部VFTO最大值发生在单进单出线方式8隔离开关DS23处,VFTO幅值为2.787pu。......
2023-07-02
相关推荐