容量是蓄能器的重要参数,是选择蓄能器的主要依据。不同类型或不同功用的蓄能器其计算方法也有所不同。下面以气囊式蓄能器短期大量供压力油为例介绍计算方法。蓄能器工作容积Vw 的计算这里的Vw 是蓄能器所能储存(或释放)油液的最大容积。在各个工作阶段,蓄能器释放(或储存)的油量为:ΔVi 为负值时表示释放压力油;ΔVi 为正值时则表示储存压力油。......
2025-09-29
【主要内容】
1.二元函数情形
二元函数f(x,y)在约束条件φ(x,y)=0下的极值,称为条件极值,其中f(x,y)称为目标函数.
设f(x,y),φ(x,y)都具有二阶连续偏导数,则上述的条件极值可利用拉格朗日乘数法计算,具体步骤如下:
(1)作拉格朗日函数F(x,y,λ)=f(x,y)+λφ(x,y)(其中,λ是非零常数).
(2)求解方程组
(3)检验.上述方程组的每个解都是f(x,y)在约束条件φ(x,y)=0下的可能极值点,逐一检验f(x,y)在各个可能极值点处是否能取到极大值或极小值.通常条件极值问题中计算的是最值,它可按以下方法直接得到:
如果只有一个可能极值点(x1,y1),则f(x1,y1)就是f(x,y)在φ(x,y)=0下的最值,至于是最大值还是最小值可按问题的实际意义确定;
如果有可能极值点(x1,y1),(x2,y2),…,(xn,yn),则
f(x,y)在φ(x,y)=0下的最大值=max{f(x1,y1),f(x2,y2),…,f(xn,yn)},
f(x,y)在φ(x,y)=0下的最小值=min{f(x1,y1),f(x2,y2),…,f(xn,yn)}.
2.三元函数情形
三元函数f(x,y,z)在约束条件φ(x,y,z)=0或φ1(x,y,z)=0与φ2(x,y,z)=0下的极值称为条件极值,其中f(x,y,z)称为目标函数.
设f(x,y,z),φ(x,y,z),φ1(x,y,z),φ2(x,y,z)都具有二阶连续偏导数,则上述的条件极值可用拉格朗日乘数法计算,具体步骤如下:
(1)作拉格朗日函数
F(x,y,z,λ)=f(x,y,z)+λφ(x,y,z)(λ是非零常数),或G(x,y,z,λ,μ)=f(x,y,z)+λφ1(x,y,z)+μφ2(x,y,z)(λ,μ是不全为零的常数).
(2)求解方程组 或
或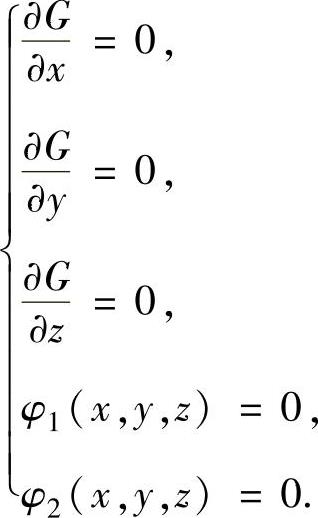
(3)检验.与二元函数情形相同.
【典型例题】
例3.6.1 (单项选择题)设f(x,y),φ(x,y)都是可微函数,且φy′(x,y)≠0.已知(x0,y0)是f(x,y)在约束条件φ(x,y)=0下的一个极值点,则下列选项中正确的是( ).
A.若fx′(x0,y0)=0,则fy′(x0,y0)=0
B.若fx′(x0,y0)=0,则fy′(x0,y0)≠0
C.若fx′(x0,y0)≠0,则fy′(x0,y0)=0
D.若fx′(x0,y0)≠0,则fy′(x0,y0)≠0
精解 利用拉格朗日乘数法可得正确选项.
记F(x,y,λ)=f(x,y)+λφ(x,y),并记对应点(x0,y0)的λ值为λ0,则由题设知(x0,y0)是f(x,y)在φ(x,y)=0下的一个极值点.所以 即
即 消去其中的λ0得fx′(x0,y0)φy′(x0,y0)-fy′(x0,y0)φx′(x0,y0)=0.
消去其中的λ0得fx′(x0,y0)φy′(x0,y0)-fy′(x0,y0)φx′(x0,y0)=0.
由此可知,当fx′(x0,y0)≠0时,由φy′(x0,y0)≠0得fy′(x0,y0)≠0.
因此本题选D.
例3.6.2 求二元函数z=x2+y2+5在约束条件y=1-x下的极值.
精解 由于是计算z在y=1-x下的极值,所以将y=1-x代入z,转换成一元函数,再计算极值.(https://www.chuimin.cn)
将y=1-x代入z得z=x2+(1-x)2+5=2x2-2x+6.
由于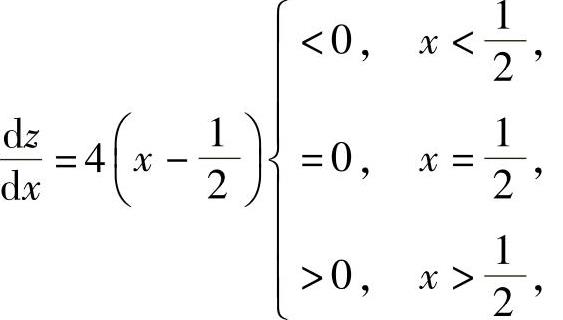 所以z=2x2-2x+6在
所以z=2x2-2x+6在 处取得极小值.因此,二
处取得极小值.因此,二
元函数z=x2+y2+5在约束条件y=1-x下有极小值 ,无极大值.
,无极大值.
例3.6.3 求二元函数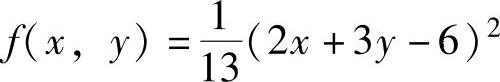 在约束条件x2+4y2=4下的极值.
在约束条件x2+4y2=4下的极值.
精解 用拉格朗日乘数法求解.
记F(x,y,λ)=f(x,y)+λφ(x,y) (其中φ(x,y)=x2+4y2-4) ,
,
则 ,
, 于是方程组
于是方程组 即
即
由式(1)和式(2)消去λ得 代入式(3)得
代入式(3)得 ,
, ,即f(x,y)在约束条件φ(x,y)=0下的可能极值点为
,即f(x,y)在约束条件φ(x,y)=0下的可能极值点为 和
和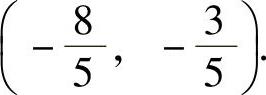
下面判别它们是否为极值点.
x2+4y2=4的两边对x求导得d
d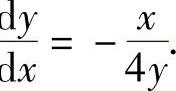 于是
于是
由此得到
所以,f(x,y)在约束条件φ(x,y)=0下,有极小值 ,有极大值
,有极大值
例3.6.4 将正数a分为三个小正数之和,使它们的乘积为最大,求这三个小正数.
精解 设三个小正数为x,y,z,则本题即为在约束条件x+y+z=a下计算三元函数z=xyz(0<x<a,0<y<a,0<z<a)的最小值,故可应用拉格朗日乘数法.
记F(x,y,z,λ)=xyz+λ(x+y+z-a),则Fx′=yz+λ,Fy′=xz+λ,Fz′=xy+λ.于是方程组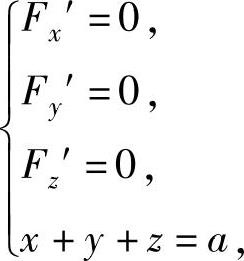 即
即
由式(1)、式(2)和式(3)知x=y=z.将它代入式(4)得 ,即xyz在
,即xyz在
x+y+z=a下只有一个可能极值点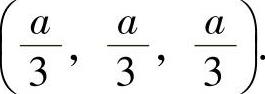
由于现在要计算的是约束条件下的最大值,因此它必在 处取到,即乘积
处取到,即乘积
为最大的三个小正数应都为
例3.6.5 求二元函数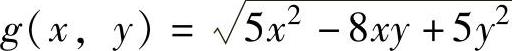 在约束条件x2+y2-xy=75下的最大值.
在约束条件x2+y2-xy=75下的最大值.
精解 本题应使用拉格朗日乘数法求解,但函数g(x,y)的表达式比较复杂,不易求解,所以需对目标函数作些转换.考虑 ,并将x2+y2-xy=75代入化简,由此得到的目标函数记为h(x,y),显然在x2+y2-xy=75下g(x,y)与h(x,y)有相同的最大值点.由于
,并将x2+y2-xy=75代入化简,由此得到的目标函数记为h(x,y),显然在x2+y2-xy=75下g(x,y)与h(x,y)有相同的最大值点.由于 ,所以作拉格朗日函数
,所以作拉格朗日函数
H(x,y)=(125-xy)+λ(x2+y2-xy-75),
则Hx′=2λx-(1+λ)y,Hy′=2λy-(1+λ)x.于是方程组 即
即
式(1)+式(2)得(λ-1)(x+y)=0,即λ=1,x=-y.
当λ=1时,由式(1)得x=y.代入式(3)得 ;当x=-y时,代入式(3)得
;当x=-y时,代入式(3)得
x=-y=±5.于是在约束条件x2+y2-xy=75下,h(x,y)的可能极值点为 ,
, ,M3(5,-5),M4(-5,5).
,M3(5,-5),M4(-5,5).
由于 ,h(5,-5)=h(-5,5)=150,
,h(5,-5)=h(-5,5)=150,
所以g(x,y)在约束条件x2+y2-xy=75下的最大值为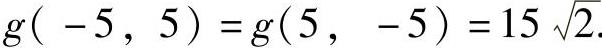
相关文章

容量是蓄能器的重要参数,是选择蓄能器的主要依据。不同类型或不同功用的蓄能器其计算方法也有所不同。下面以气囊式蓄能器短期大量供压力油为例介绍计算方法。蓄能器工作容积Vw 的计算这里的Vw 是蓄能器所能储存(或释放)油液的最大容积。在各个工作阶段,蓄能器释放(或储存)的油量为:ΔVi 为负值时表示释放压力油;ΔVi 为正值时则表示储存压力油。......
2025-09-29

定义 设函数z=f(x,y)在点(x0,y0)的某个邻域内有定义,对于该邻域内异于点(x0,y0)的点(x,y):(1)若f(x,y)<f(x0,y0),则称函数在点(x0,y0)有极大值f(x0,y0);(2)若f(x,y)>f(x0,y0),则称函数在点(x0,y0)有极小值f(x0,y0).极大值、极小值统称为极值.使函数取得极值的点称为极值点.例1 函数z=3x2+4y2在点(0,0)处有......
2025-09-30

由图1-41可见,Vo1、Vo2、Vo3为主输出,主输出电路分别引出3路反馈控制信号;Vo4和Vo5是辅助输出,采用正负对称输出电路,未加反馈控制。总的反馈电流为图1-41 多路输出开关电源原理图图1-42 Vo1、Vo2、Vo33路同时提供反馈的电路输出总电流为Io=Io1+Io2+Io3=2A+1.2A+1A=4.2A反馈比例系数K1、K2、K3分别为各组反馈电流IF1、IF2、IF3分别为各组反馈电阻R4、R5、R6的阻值分别为上述计算方法是计算多路输出开关电源反馈电阻的一种既简便又精确的方法。......
2025-09-29

断路器操作机构的疲劳问题主要是由闭合与分断过程中的动态应力应变引起,因此对断路器操作机构疲劳寿命评估的前提是分合闸过程中零部件动态应力应变的准确计算。动态应力应变的计算基于柔性体的瞬态动力学分析,瞬态动力学分析是用于确定结构在承受任意随时间变化的载荷时的动力学响应的一种方法。常用的瞬态动力学求解方法包括:完全法、缩减法、模态叠加法,本章中柔性体应力应变的计算使用模态叠加法。......
2025-09-29

任何采用焊接方法制造的锅炉、压力容器产品均要涉及焊接材料定额的计算和预估。表10-15 不同焊接方法的焊接材料定额损耗系数推荐根据以上计算公式,焊接材料定额计算工作似乎不难。焊接材料定额卡样表设计见表10-17。......
2025-09-29

气压给水设备气压给水设备与水塔或高位水箱的功能同等;兼有升压、调节、贮水、供水、蓄能和控制水泵启停的功能,由气压水罐、水泵机组、管路系统、电控系统、气体调节控制系统、自动控制箱组成。......
2025-09-30

(三)T形接头的静载强度计算1.载荷平行于T形接头焊缝的强度计算这类T形接头在焊接时有两种坡口形式,其一是开I形坡口时,计算公式为:其二是开坡口并熔透,强度应按对接接头计算,焊缝金属横截面积A=δh,由于焊缝最上端是产生最大应力的危险点,在这点将同时有两个切应力作用,一个是由F力引起的τF,另一个是由M=FL引起的τM。......
2025-09-29

由上面的例子可以总结出计算梁的剪力和弯矩的具体方法:剪力FQ=截面一侧所有外力的代数和,外力的正负号规定可简记为“左上右下,剪力为正”。试求指定截面上的剪力和弯矩。弯矩的突变值等于集中力偶的力偶矩的大小。因此,应用截面法计算任意截面的弯矩时,截面不能选取在集中力偶作用的截面上。......
2025-09-29
相关推荐