,,则f(x,y)在φ(x,y)=0下的最大值=max{f,f,…......
2023-10-27
【主要内容】
1.二元函数极值的定义
设二元函数f(x,y)在点(x0,y0)的某个邻域内有定义.如果在此邻域内对任意(x,y)≠(x0,y0)都有
f(x,y)<f(x0,y0)(或f(x,y)>f(x0,y0)),则称f(x0,y0)是f(x,y)的一个极大值(或极小值),称(x0,y0)为f(x,y)的极大值点(或极小值点).极大值与极小值总称极值,极大值点与极小值点总称极值点.
2.二元函数极值存在的必要条件
设二元函数f(x,y)在点(x0,y0)处有偏导数,则它在点(x0,y0)处取得极值的必要条件为
fx′(x0,y0)=0且fy′(x0,y0)=0(称满足fx′(x,y)=0且fy′(x,y)=0的点(x0,y0)为f(x,y)的驻点).
注 函数极值的必要条件可以推广.
设二元函数f(x,y)在点(x0,y0)的某个邻域内有定义,则它在点(x0,y0)处取得极值的必要条件为
fx′(x0,y0)=0(或不存在)且fy′(x0,y0)=0(或不存在).
由此可知,对于二元函数f(x,y),它的可能极值点来自三个方面:
(ⅰ)使fx′(x,y),fy′(x,y)都为零的点;
(ⅱ)使fx′(x,y)为零而fy′(x,y)不存在或者使fy′(x,y)为零而fx′(x,y)不存在的点;
(ⅲ)使fx′(x,y),fy′(x,y)都不存在的点.
3.二元函数极值的充分条件
设二元函数f(x,y)在点(x0,y0)的某个邻域内有二阶连续偏导数且
fx′(x0,y0)=fy′(x0,y0)=0.记A=fx″x(x0,y0),B=fx″y(x0,y0),C=fy″y(x0,y0),则
(1)当AC-B2>0时,f(x0,y0)是f(x,y)的一个极值,且当A>0时,是极小值,当A<0时,是极大值.
(2)当AC-B2<0时,f(x0,y0)不是极值.
(3)当AC-B2=0时,f(x0,y0)是否为极值需具体讨论(一般地,通过极值的定义讨论).
4.二元函数极值的计算步骤
二元函数f(x,y)的极值可按以下步骤计算:
(1)确定f(x,y)的定义域D(设f(x,y)在D上有二阶连续偏导数);
(2)计算f(x,y)在D上的所有驻点,记为(x1,y1),(x2,y2),…,(xn,yn);
(3)逐一判断各个驻点是否为极值点,如果是极值点,则同时确定其是极大值点还是极小值点,并求出对应的极大值或极小值.
【典型例题】
例3.5.1 (单项选择题)已知二元函数f(x,y)在点(0,0)的某个邻域内连续,且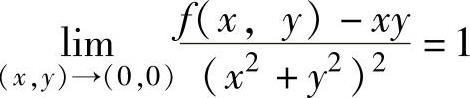 ,则( ).
,则( ).
A.(0,0)不是f(x,y)的极值点
B.(0,0)是f(x,y)的极大值点
C.(0,0)是f(x,y)的极小值点
D.无法判定(0,0)是否为f(x,y)的极值点
精解 可由二元函数极值的定义进行判定.
由题设知,在点(0,0)的充分小邻域内有
f(x,y)=xy+(x2+y2)2+o((x2+y2)2).由此可知,在点(0,0)的充分小邻域内,存在使f(x,y)>0的点,也有使f(x,y)<0的点.所以,(0,0)不是f(x,y)的极值点.
因此本题选A.(www.chuimin.cn)
例3.5.2 求二元函数z=x4+y4-x2-2xy-y2的极值.
精解 二元函数在整个xOy平面上有定义,且在其上有二阶连续偏导数,
zx′=4x3-2x-2y,zy′=4y3-2x-2y,
A(x,y)=zx″x=12x2-2,B(x,y)=zx″y=-2,C(x,y)=zy″y=12y2-2.
方程组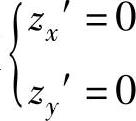
,
{,即 ,的第一个方程减去第二个方程得y=x.将它代入第
,的第一个方程减去第二个方程得y=x.将它代入第
一个方程得
4x3-4x=0,即 x=-1,1,0.对应地有y=-1,1,0.所以f(x,y)有驻点
(-1,-1),(1,1),(0,0).
由于A(-1,-1)=10>0,且(AC-B2)(-1,-1)=96>0,所以z(-1,-1)=-2是极小值.同样z(1,1)=-2也是极小值.
由于(AC-B2)(0,0)=0,所以需用其他方法讨论z(0,0)是否为极值.因为z=x4+y4-(x+y)2,所以在点(0,0)的充分小去心邻域内,当x+y=0时,z>0;当x+y≠0时,z<0,因此z(0,0)不是极值.
例3.5.3 求二元函数f(x,y)=x2(2+y2)+ylny的极值.
精解 f(x,y)在其定义域y>0上二阶连续可导,且
fx′(x,y)=2x(2+y2),fy′(x,y)=2x2y+lny+1,
A(x,y)=fx″x(x,y)=4+2y2,B(x,y)=fx″y=4xy,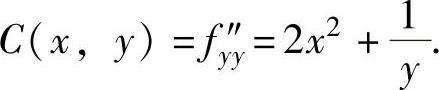
由方程组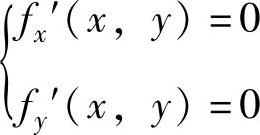
,
{,即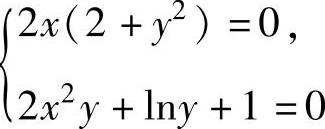
知f(x,y)有唯一驻点
由于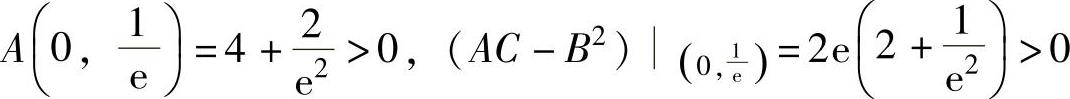 ,所以
,所以 是f(x,y)的极小值,f(x,y)无极大值.
是f(x,y)的极小值,f(x,y)无极大值.
例3.5.4 设二元函数z=z(x,y)由方程2x2+y2+z2+2xy-2x-2y-4z+4=0确定,求z=z(x,y)的极值.
精解 本题的z=z(x,y)虽然是二元隐函数,但它的极值的计算方法却与二元显函数z=f(x,y)相同.
所给方程两边分别对x,y求偏导数得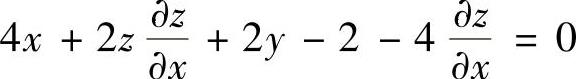 ,即
,即 ,(1)
,(1)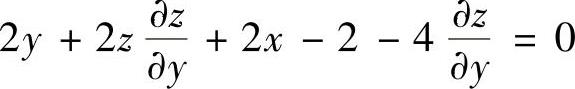 ,即
,即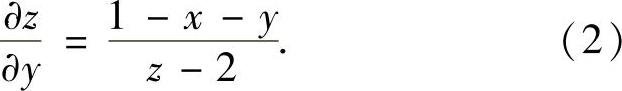
由 即
即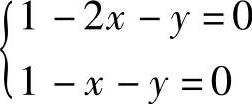 ,得x=0,y=1,对应的函数值为z=1,3.
,得x=0,y=1,对应的函数值为z=1,3.
由式(1)和式(2)得 ,
,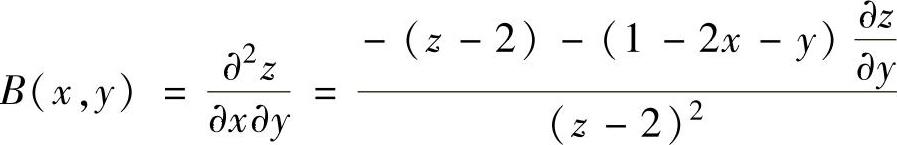 ,
,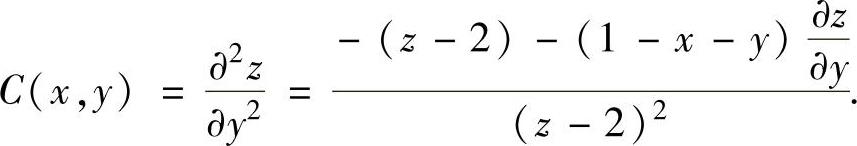
当x=0,y=1,z=1时,有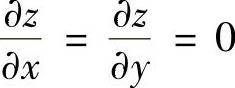 且
且
A(0,1)=2>0,(AC-B2)(0,1)=2·1-12=1>0,所以z=z(x,y)在点(0,1)处取到极小值z=1.
当x=0,y=1,z=3时,有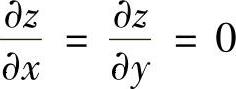 ,此时
,此时
A(0,1)=-2<0,(AC-B)2(0,1)=(-2)·(-1)-(-1)2=1>0,
所以z=z(x,y)在点(0,1)处取到极大值z=3.
注 由式(1)和式(2)可知,z=2也可能是z=z(x,y)的极值.由于z=2时,所给方程成为
2x2+y2+2xy-2(x+y)=0,即x2+(x+y-1)2=1.
由此可知,z=z(x,y)在曲线x2+(x+y-1)2=1上取值为2,从而z=2不可能是z=z(x,y)的极值.
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

定义 设函数z=f(x,y)在点(x0,y0)的某个邻域内有定义,对于该邻域内异于点(x0,y0)的点(x,y):(1)若f(x,y)<f(x0,y0),则称函数在点(x0,y0)有极大值f(x0,y0);(2)若f(x,y)>f(x0,y0),则称函数在点(x0,y0)有极小值f(x0,y0).极大值、极小值统称为极值.使函数取得极值的点称为极值点.例1 函数z=3x2+4y2在点(0,0)处有......
2023-10-19

5.曲线L:xy=1(x>0)上求一点,使函数f(x,y)=x2+2y2达到最小值.复习题八一、填空题二、选择题4.设z=xy,则dz=().A.dx+dyB.-dx-dyC.xdx+ydyD.yd......
2023-11-20

本节将基于随机过程理论和Rice公式对随机车流作用下悬索桥加劲梁的位移响应极值概率分布进行研究。因此,对于随机车流样本作用下桥梁结构响应的极值预测的关键就是证明其响应值为高斯平稳过程。采用样本函数的均值作为位移响应随机过程的均值,取时间间隔为τ,式中相关参数表达式为:在得到界限跨越率之后,即可按照极值分布函数构建最大值的概率分布函数。......
2023-09-19

微分方程虽然也不是很好解,但是相对于解泛函已经要容易许多了。参考阅读//No. 9 映射,第22页No. 50 导数,第104页No. 55 微分方程,第114页No. 66 极小曲面,第136页右图:当一个函数达到最大值或者最小值时,它的导数为零。通常来讲,要解决一个泛函问题,我们就把它转化为一个有希望解决的微分方程问题。......
2023-11-22

剪切试验试件的受力情况应模拟零件的实际工作情况进行。若以A 表示销钉横截面面积,则应力为τ 与剪切面相切,故为切应力。以上计算是以假设“切应力在剪切面上均匀分布”为基础的,实际上它只是剪切面内的一个“平均切应力”,所以也称为名义切应力。当F 达到Fb 时的切应力称剪切极限应力,记为τb。对于图5-8 所示的剪切试验,剪切极限应力为用τb 除以安全系数n,即得到许用切应力这样,剪切计算的强度条件可表示为......
2023-06-19

图7-1简单供电网如果线路中输送的功率一直保持为最大负荷功率Smax,在τh内的能量损耗恰等于线路全年的实际电能损耗,则称τ为最大负荷损耗时间。若认为电压接近于恒定,则由上式可见,最大负荷损耗时间τ与用视在功率表示的负荷曲线有关。试求线路及变压器中全年的电能损耗。对于已运行电网的能量损耗计算,此方法的误差太大,不宜采用。......
2023-06-15
相关推荐