【主要内容】1.二元函数极限与连续的概念设二元函数f（x，y）在点（x0，y0）的某个去心邻域{（x，y）|0<（x-x0）2+（y-y0）2<δ2}（其中，δ是某正数）内有定义.如果动点（x，y）以任何方式无限趋于点（x0，y0）时，f（x，y）总是无限趋于常数A，则称A是点（x，y）趋于点（x0，y0）（记为（x，y）→（x0，y0））时f（x，y）的极限，记为或注 根据定义，可以按以下方法判......
2023-10-27
二元隐函数偏导及二阶偏导计算
【摘要】：【主要内容】1.二元隐函数偏导数的计算设二元函数z=z（x，y）由方程F（x，y，z）=0确定，则称z=z（x，y）是二元隐函数.它的偏导数可按以下步骤计算：（1）所给方程两边对x（或y）求偏导数（此时应注意z是关于x与y的二元函数）得；（2）解上述以为未知数的方程，即得注 关于方程F（x，y，z）=0确定隐函数z=z（x，y）有以下的隐函数定理：设F（x，y，z）在点（x0，y0，z0）的某个邻
【主要内容】
1.二元隐函数偏导数的计算
设二元函数z=z（x，y）由方程F（x，y，z）=0确定，则称z=z（x，y）是二元隐函数.它的偏导数可按以下步骤计算：
（1）所给方程两边对x（或y）求偏导数（此时应注意z是关于x与y的二元函数）得
；
（2）解上述以
为未知数的方程，即得
注 关于方程F（x，y，z）=0确定隐函数z=z（x，y）有以下的隐函数定理：
设F（x，y，z）在点（x0，y0，z0）的某个邻域内有连续偏导数，并且F（x0，y0，z0）=0，Fz′（x0，y0，z0）≠0，则方程F（x，y，z）=0在点（x0，y0，z0）的某个邻域内确定唯一的具有连续偏导数的函数z=z（x，y），它还满足z0=z（x0，y0）及F（x，y，z（x，y））≡0.
2.二元隐函数二阶偏导数的计算
二元隐函数的二阶偏导数，可以对已求得的一阶偏导数再求偏导数得到.
【典型例题】(www.chuimin.cn)
例3.4.1 设二元函数z=z（x，y）由方程
确定，求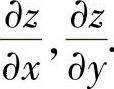
精解 所给方程两边求全微分得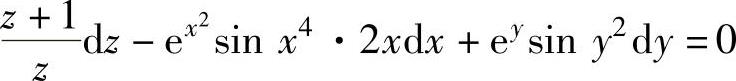
即
所以，
注 由于本题需计算
，所以不是从对所给方程两边分别求关于x和关于y的偏导数入手，而是从对所给方程两边求全微分入手.
例3.4.2 设二元函数z=z（x，y）由方程f（x+y，y+z）=0确定，其中，函数f（u，v）具有二阶连续偏导数，且fv′≠0.求zx″x.
精解 由二元隐函数求偏导数方法先算出zx′，然后计zx″x.
记u=x+y，v=y+z，在所给方程两边对x求偏导数得fu′+fv′zx′=0， 即
于是，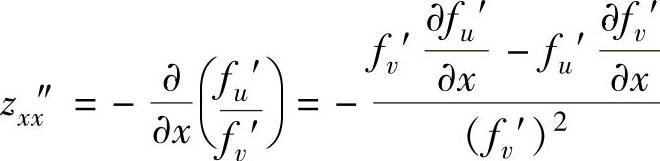
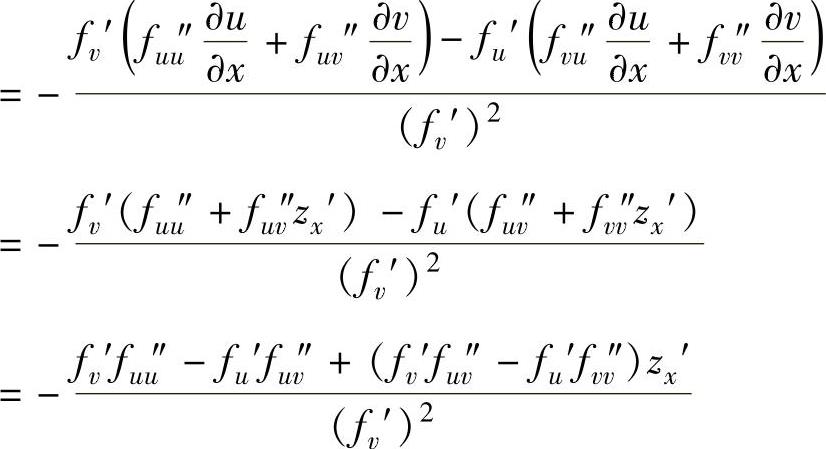
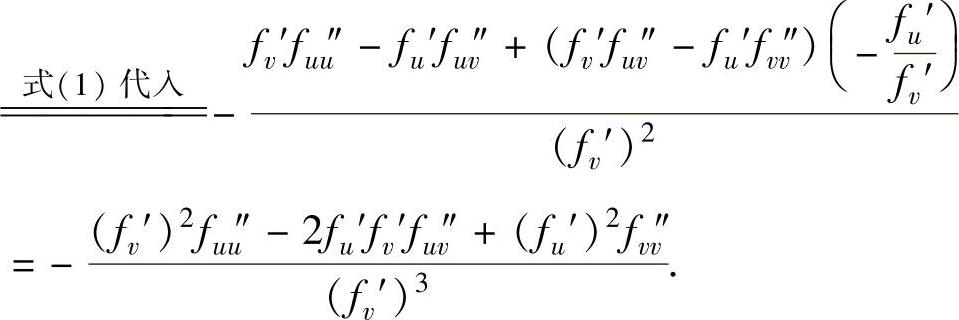
有关2015考研数学（三）基础篇全面复习与常考知识点解析的文章
- 详细阅读
-
计算二元复合函数的偏导数与二阶偏导数详细阅读
【主要内容】设二元函数u=u（x，y），v=v（x，y）在点（x，y）处偏导数存在，函数z=f（u，v）在对应点（u，v）处可微，则复合函数z=f（u（x，y），v（x，y））在点（x，y）处的偏导数存在，且二元以上复合函数的偏导数也有类似的计算公式.注 在计算二元或二元以上复合函数的偏导数时，应先画出复合函数的关系图，然后按此图用复合函数求偏导数公式计算.例如，二元复合函数z=f（u（x，y），......
2023-10-27
-
复合函数、反函数及隐函数导数计算详细阅读
【主要内容】计算函数的导数的基础是求导基本公式和四则运算法则.求导基本公式：（1）C′=0（C是常数），（2）（xμ）′=μxμ-1，（3）（ax）′=axlna（常数a>0但a≠1），特别地，（ex）′=ex，（4），特别地，，（5）（sinx）′=cosx， （6）（cosx）′=-sinx，（7）（tanx）′=sec2x， （8）（cotx）′=-csc2x，（9）（secx）′=secx......
2023-10-27
-
高考数学题解析：三角恒等变换、导函数与函数的详细阅读
其中正确的是__________..10.已知函数f=sin x+cos x，f′是f的导函数.若f=2f′，则=__________.......
2023-10-15
-
带钢液压跑偏控制简述详细阅读
轧机作业线上带钢纵向高速运行时，带钢的中心线或带钢的边缘会向两侧偏移，这种现象称为跑偏。带钢跑偏必须限制在一定的公差范围内，否则就会刮坏设备或使得带材边缘损坏，影响成品质量，跑偏严重时还会导致不能正常生产，所以带钢跑偏控制是带材连续作业线上必不可少的环节。4）光电液伺服系统：采用光电检测器将跑偏信号检测出来并经过放大器放大，控制电液伺服阀推动液压缸进行纠偏。......
2023-06-15
-
光纤导光原理简介详细阅读
波动光学是把光纤中的光作为经典电磁场来处理。图9.6为阶跃光纤的子午光线，一般将通过光纤轴线的平面称为子午面，把传输中总是位于子午面内的光线称为子午光线。为此，人们研制了渐变折射率光纤。多模渐变折射率光纤的射线光学理论分析多模渐变折射率光纤纤芯中的折射率是连续变化的。采用渐变光纤的目的是减小多模光纤的模式色散。在光纤的分析中，求上述亥姆霍兹方程满足边界条件的解，即可得到光纤中的场的解答。......
2023-06-26
- 详细阅读
-
隐函数存在定理1及推导详细阅读
隐函数存在定理1 设函数F（x，y）在点P（x0，y0）的某一邻域内具有连续的偏导数，且F（x0，y0）=0，Fy（x0，y0）≠0，则方程F（x，y）=0在点（x0，y0）的某一邻域内恒能唯一确定一个单值连续且具有连续导数的函数y=f（x），它满足条件y0=f（x0），并有式（8.5.2）就是隐函数的求导公式.这个定理我们不证.现仅就式（8.5.2）作如下推导.将方程（8.5.1）所确定的函数y......
2023-10-19
相关推荐