【主要内容】1.二元函数极限与连续的概念设二元函数f(x,y)在点(x0,y0)的某个去心邻域{(x,y)|0<(x-x0)2+(y-y0)2<δ2}(其中,δ是某正数)内有定义.如果动点(x,y)以任何方式无限趋于点(x0,y0)时,f(x,y)总是无限趋于常数A,则称A是点(x,y)趋于点(x0,y0)(记为(x,y)→(x0,y0))时f(x,y)的极限,记为或注 根据定义,可以按以下方法判......
2023-10-27
【主要内容】
设二元函数u=u(x,y),v=v(x,y)在点(x,y)处偏导数存在,函数z=f(u,v)在对应点(u,v)处可微,则复合函数z=f(u(x,y),v(x,y))在点(x,y)处的偏导数存在,且
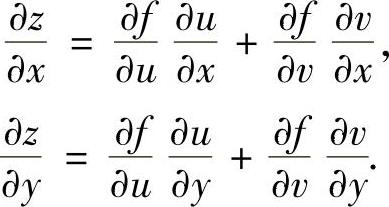
二元以上复合函数的偏导数也有类似的计算公式.
注 在计算二元或二元以上复合函数的偏导数时,应先画出复合函数的关系图,然后按此图用复合函数求偏导数公式计算.例如,二元复合函数z=f(u(x,y),v(x))的关系图为
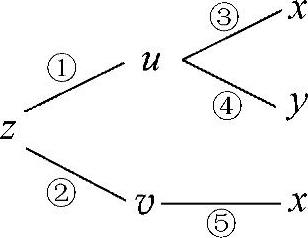
由关系图可见,z与x之间有两条通路:①—③,②—⑤,所以
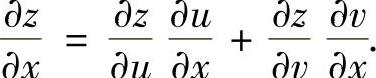
复合函数f的二阶偏导数可以通过对已求得的一阶偏导数再求偏导数得到,但当复合函数f是抽象函数时,对一阶偏导数再求偏导数时总是认为一阶偏导数有与复合函数f本身相同的复合函数关系图.
【典型例题】
例3.3.1 设z=f(exsiny,x2+y2),其中,二元函数f(u,v)具有二阶连续偏导数,求 ,
,
精解 由于u=exsiny,v=x2+y2,所以z与x,y的复合函数关系图如图3.3.1所示,由图可知,

图 3.3.1
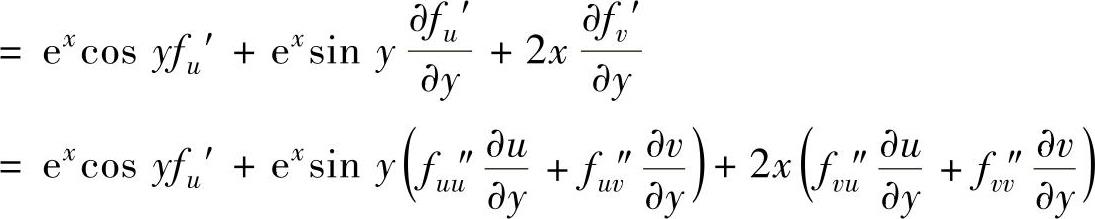 (可以认为fu′,fv′都有与f同样的复合函数关系图)=excosyfu′+exsiny(excosyfuu″+2yfuv″)+2x(excosyfuv″+2yfvv″)=excosyfu′+e2xsinycosyfuu″+2ex(ysiny+xcosy)fuv″+4xyfvv″.
(可以认为fu′,fv′都有与f同样的复合函数关系图)=excosyfu′+exsiny(excosyfuu″+2yfuv″)+2x(excosyfuv″+2yfvv″)=excosyfu′+e2xsinycosyfuu″+2ex(ysiny+xcosy)fuv″+4xyfvv″.
例3.3.2 设二元函数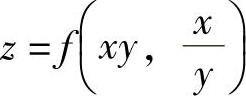 ,其中,f(u,v)有二阶连续偏导数,求
,其中,f(u,v)有二阶连续偏导数,求
精解 先算出 ,然后计算
,然后计算 的全微分,从而确定
的全微分,从而确定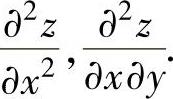
记u=xy,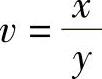 ,则z与x,y的复合函数关系如图3.3.2所示.
,则z与x,y的复合函数关系如图3.3.2所示.
由图可知,
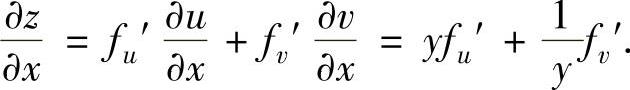
由此可得

图 3.3.2

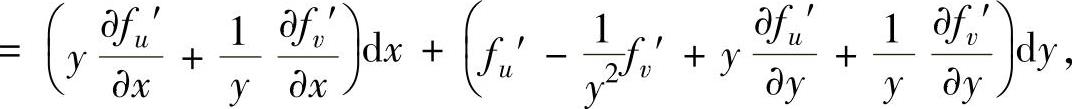
所以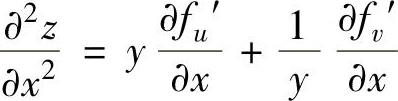
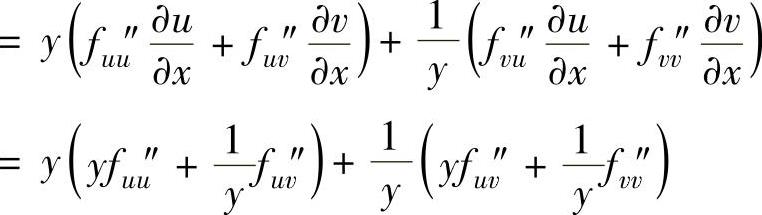
 ,(www.chuimin.cn)
,(www.chuimin.cn)

注 在同时计算二元复合函数z=f(u(x,y),v(x,y))的 ,
, 时,可利用全微分形
时,可利用全微分形
式不变性,从计算dz入手较为快捷,同样在同时计算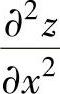 ,
,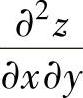 时,可从计算
时,可从计算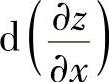 入手.
入手.
例3.3.3 设f(u,v)具有二阶连续偏导数,且满足fx″x+fy″y=1,又g(x,y)=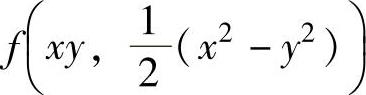 ,求gx″x+gy″y.
,求gx″x+gy″y.
精解 先算出gx″x,gy″y,然后利用fx″x+fy″y=1计算gx″x+gy″y.
记u=xy,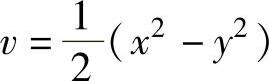 ,则g(x,y)的复合函数关系如图3.3.3所示.
,则g(x,y)的复合函数关系如图3.3.3所示.
于是由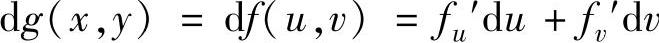
得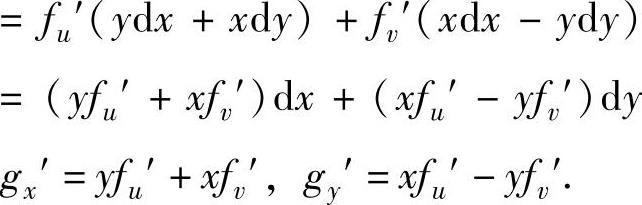
从而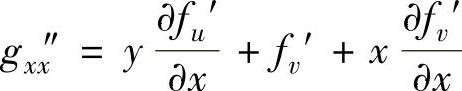

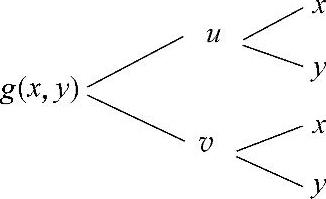
图 3.3.3
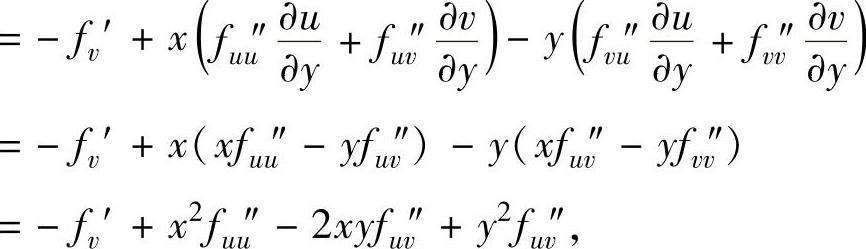
由此得到
gx″x+gy″y=(x2+y2)(fu″u+fv″v)=x2+y2
(利用题设fx″x+fy″y=1,即fu″u+fv″v=1).
例3.3.4 设二元函数u=u(x,y)有连续的二阶偏导数,并满足 ,且u(x,2x)=x,ux′(x,2x)=x2.求ux″x(x,2x),ux″y(x,2x).
,且u(x,2x)=x,ux′(x,2x)=x2.求ux″x(x,2x),ux″y(x,2x).
精解 先计算dux′(x,2x)得到一个关于ux″x(x,2x)与ux″y(x,2x)的关系式.再由u(x,2x)=x得到另一个关于ux″x(x,2x)与ux″y(x,2x)的关系式.
由于 dux′(x,2x)=ux″x(x,2x)dx+ux″y(x,2x)·2dx
=[ux″x(x,2x)+2ux″y(x,2x)]dx,另一方面,由题设ux′(x,2x)=x2得dux′(x,2x)=2xdx,所以
ux″x(x,2x)+2ux″y(x,2x)=2x.(1)
对u(x,2x)=x两边求全微分得
ux′(x,2x)dx+2uy′(x,2x)dx=dx,即 ux′(x,2x)+2uy′(x,2x)=1.上式两边对x求偏导数得
ux″x(x,2x)+2ux″y(x,2x)+2uy″x(x,2x)+4uy″y(x,2x)=0,即5ux″x(x,2x)+4ux″y(x,2x)=0(2)
(由于u有二阶连续偏导数,所以ux″y=uy″x,此外由题设知uy″y=ux″x).
将式(1)和式(2)联立得 从而由式(1)得
从而由式(1)得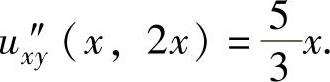
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

【主要内容】1.二元函数极限与连续的概念设二元函数f(x,y)在点(x0,y0)的某个去心邻域{(x,y)|0<(x-x0)2+(y-y0)2<δ2}(其中,δ是某正数)内有定义.如果动点(x,y)以任何方式无限趋于点(x0,y0)时,f(x,y)总是无限趋于常数A,则称A是点(x,y)趋于点(x0,y0)(记为(x,y)→(x0,y0))时f(x,y)的极限,记为或注 根据定义,可以按以下方法判......
2023-10-27

【主要内容】1.二元隐函数偏导数的计算设二元函数z=z(x,y)由方程F(x,y,z)=0确定,则称z=z(x,y)是二元隐函数.它的偏导数可按以下步骤计算:(1)所给方程两边对x(或y)求偏导数(此时应注意z是关于x与y的二元函数)得;(2)解上述以为未知数的方程,即得注 关于方程F(x,y,z)=0确定隐函数z=z(x,y)有以下的隐函数定理:设F(x,y,z)在点(x0,y0,z0)的某个邻......
2023-10-27

一、偏导数的概念【知识点回顾】y=f(x)在x=x0处导数的定义:设函数y=f(x)在点x0的某一邻域内有定义,当自变量x在x0处有增量Δx(x+Δx也在该邻域内)时,相应地,函数有增量Δy=f(x0+Δx)-f(x0),若Δy与Δx之比有当Δx→0时极限存在,则称这个极限值为y=f(x)在x0处的导数.记为基本初等函数的导数公式如下:(1)(c)′=0(c为常数)(2)(xμ)′=μxμ-1(......
2023-11-20

【主要内容】计算函数的导数的基础是求导基本公式和四则运算法则.求导基本公式:(1)C′=0(C是常数),(2)(xμ)′=μxμ-1,(3)(ax)′=axlna(常数a>0但a≠1),特别地,(ex)′=ex,(4),特别地,,(5)(sinx)′=cosx, (6)(cosx)′=-sinx,(7)(tanx)′=sec2x, (8)(cotx)′=-csc2x,(9)(secx)′=secx......
2023-10-27

一、导数的四则运算法则法则1:两个可导函数的和(差)的导数等于这两个函数的导数的和(差).用公式可写为:(u±v)′=u′±v′.其中u、v为可导函数.法则2:在求一个常数与一个可导函数的乘积的导数时,常数因子可以提到求导记号外面去.用公式可写为:(cu)′=cu′.法则3:两个可导函数乘积的导数等于第一个因子的导数乘第二个因子,加上第一个因子乘第二个因子的导数.用公式可写为:(uv)′=u′v+......
2023-11-20

y=abxn即特别地,在式中取b=1,有在式中取a=e,有再在上式中取b=1,有例3求y=(1+x)μ(μ∈R)的n阶导数.解当μN+,则y′=μ(1+x)μ-1y″=μ(μ-1)(1+x)μ-2…......
2023-11-19

解析函数不仅有一阶导数,而且有各高阶导数,它的值也可以用函数在边界上的值通过积分来表示.但是对于一元实函数来说,它在某一区间上可导,其导数在这区域上是否连续也不一定,更不要说它有高阶导数存在了.关于解析函数的高阶导数我们有下面的定理.定理2 解析函数f(z)的导数仍为解析函数,它的n阶导数为其中C为在函数f(z)的解析区域D内围绕z0 的任何一条正向简单闭曲线,而且它的内部全含于D.证明 设z0为......
2023-10-30
相关推荐