如果圆锥的母线长为l,底面半径为r,那么圆锥侧面展开的扇形半径为________,扇形的弧长为________,圆锥的侧面积为________,圆锥的全面积为_________.1.若将半径为24cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为( ).A.3cm B.6cm C.12cm D.24cm2.已知圆锥底面圆的半径为6m,它的侧面积为60πcm2,则这个圆锥的高是( ).A.......
2025-09-29
【主要内容】
1.由曲线y=f1(x),y=f2(x)(其中,函数f1(x),f2(x)连续),直线x=a,x=b(a<b)围成的平面图形面积为
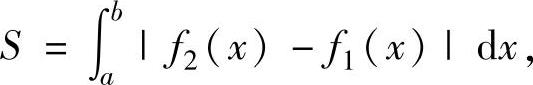
特别地,由曲线y=f(x)(其中,f(x)是非负连续函数),直线x=a,x=b(a<b)围成的平面图形(曲边梯形)面积为
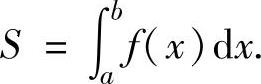
2.由曲线x=g1(y),x=g2(y)(其中,函数g1(y),g2(y)连续),直线y=c,y=d(c<d)围成的平面图形面积为
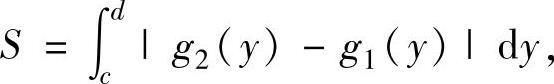
特别地,由曲线x=g(y)(其中,g(y)是非负连续函数),直线y=c,y=d(c<d)围成的平面图形(曲边梯形)面积为
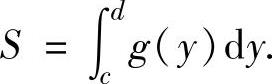
【典型例题】
例2.12.1 (单项选择题)连续函数y=f(x)在区间[-3,-2],[2,3]上的图形分别为直径是1的上、下半圆周,在区间[-2,0],[0,2]上的图形分别为直径是2的下、上半圆周(见
图2.12.1).设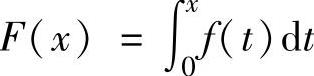 ,则下列结论正确的是( ).
,则下列结论正确的是( ).
A.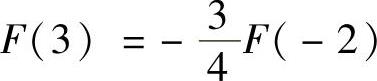
B.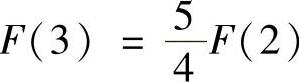
C.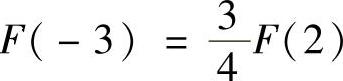
D.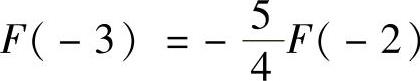
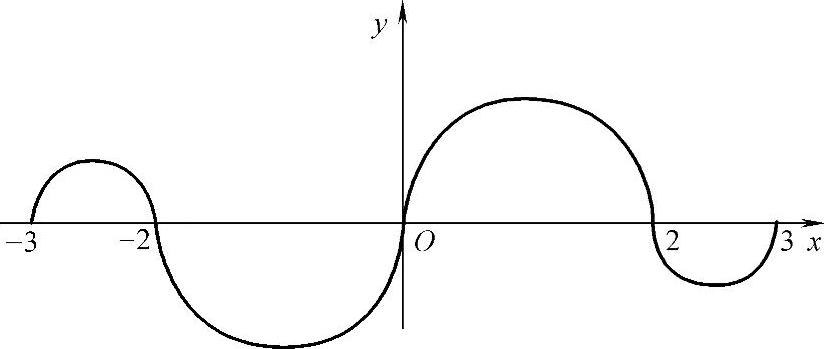
图 2.12.1
精解 算出F(3),F(-3),F(2)即可确定正确的选项.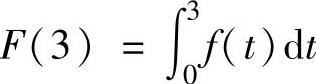 (它是[0,2]上的上半圆的面积与[2,3]上的下半圆面积的差)
(它是[0,2]上的上半圆的面积与[2,3]上的下半圆面积的差)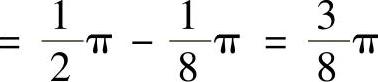 ,
,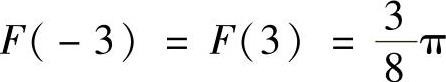 (由于f(x)是奇函数,所以F(x)是偶函数),
(由于f(x)是奇函数,所以F(x)是偶函数),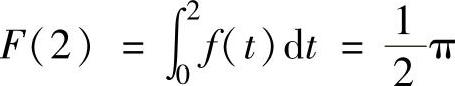 (它是[0,2]上的上半圆的面积).
(它是[0,2]上的上半圆的面积).
由此可知,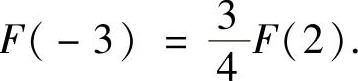
因此本题选C.
例2.12.2 求抛物线y2=2x与其上一点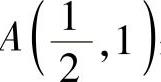 处的法线围成的平面图形D的面积S.
处的法线围成的平面图形D的面积S.
精解 先写出法线方程,然后画图计算图形D的面积S.
由于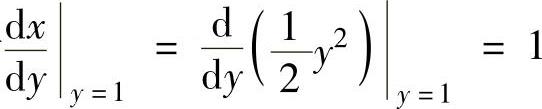 ,所以抛物
,所以抛物
线y2=2x在点A处的法线方程为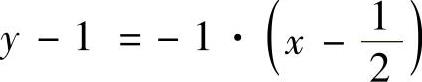 ,即
,即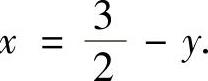
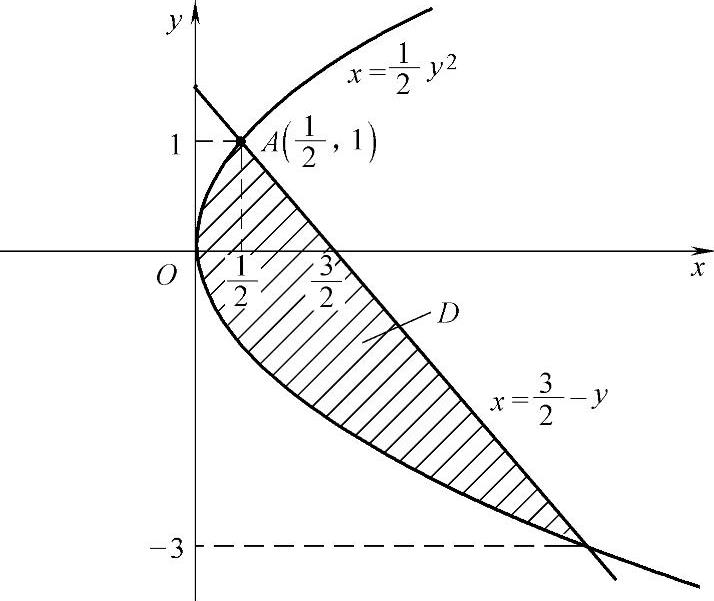
D的图形如图2.12.2所示,它是由曲线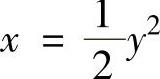 ,
,
直线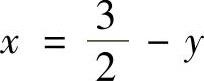 围成的,所以由该图可得
围成的,所以由该图可得
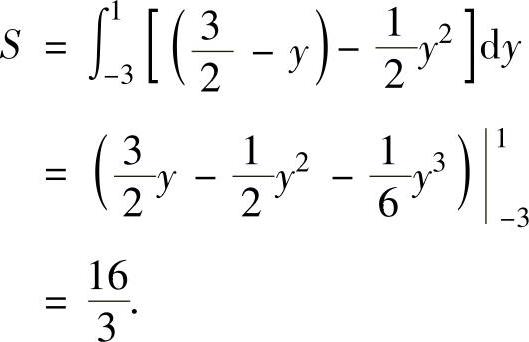
 (https://www.chuimin.cn)
(https://www.chuimin.cn)
图 2.12.2
例2.12.3 求两椭圆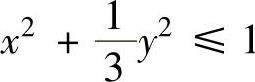 和
和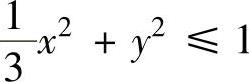 公共部分D的面积S.
公共部分D的面积S.
精解 D的图形如图2.12.3所示.由对称性知D在各个象限的面积相等,所以
S=4S1,
其中,S1是D在第一象限部分D1的面积.
记两椭圆的边界在第一象限的交点为A,则点A的坐标(x,y)满足
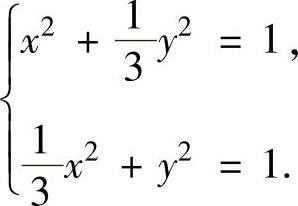
解此方程组得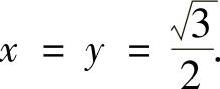
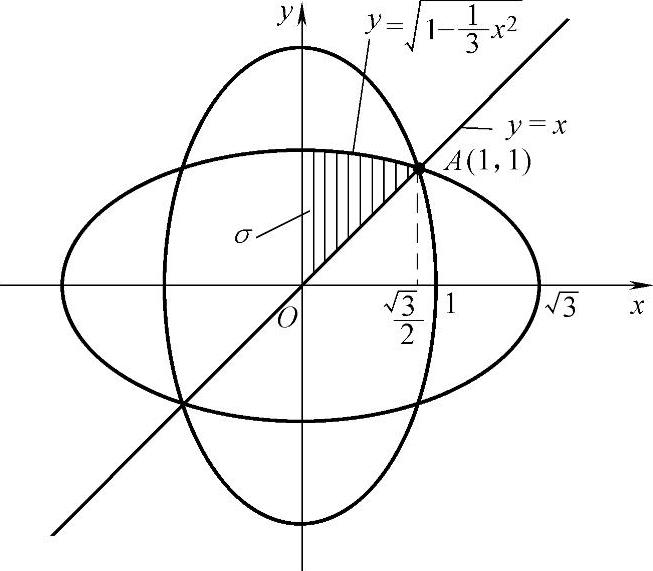
图 2.12.3
直线OA∶y=x将D1分成面积相等的两部分.记其中位于OA上方部分的面积为σ,由于
这一部分是由曲线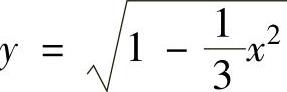 ,直线y=x和x=0围成(见图2.12.3阴影部分),所以
,直线y=x和x=0围成(见图2.12.3阴影部分),所以
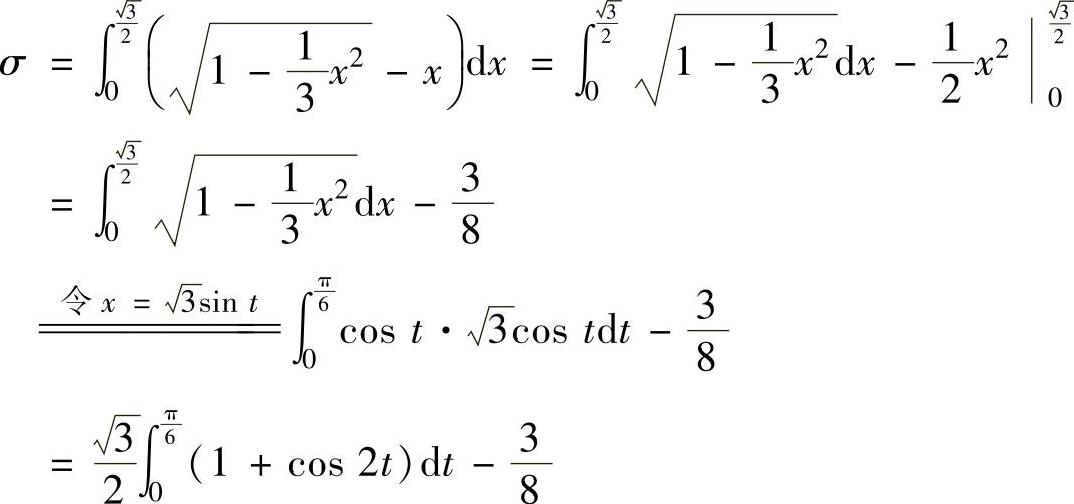
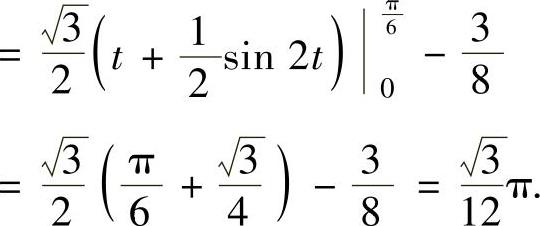
因此,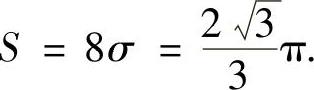
例2.12.4 设曲线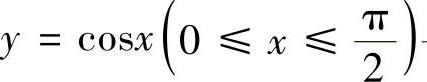 与x轴和
与x轴和
y轴围成的平面图形D被曲线y=asinx和y=bsinx(0<b<a)三等分,求常数a,b的值.
精解 图形D及曲线y=asinx,y=bsinx如图2.12.4所示.
由于D的面积为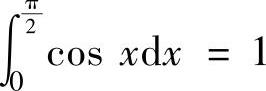 ,所以由题设知,由
,所以由题设知,由
曲线y=cosx,y=asinx及y轴围成的图形面积为
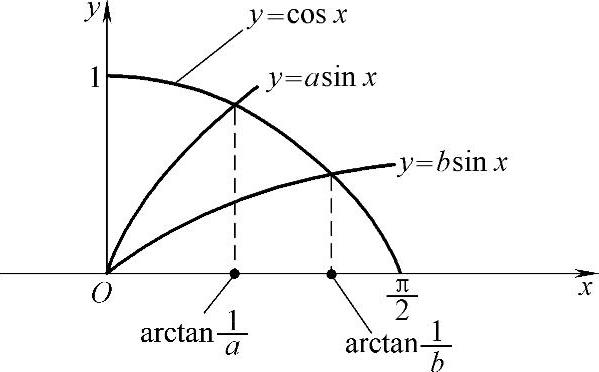
图 2.12.4
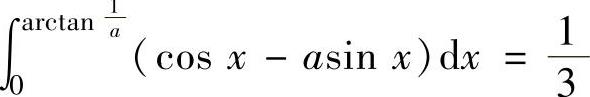 ,即
,即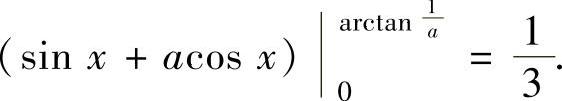
由此得到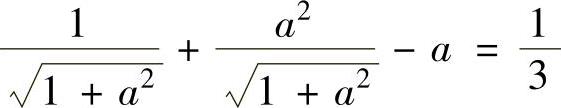 ,即
,即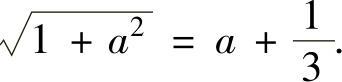
解此方程得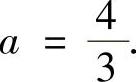
同样由题设知,由曲线y=cosx,y=bsinx及y轴围成的图形面积为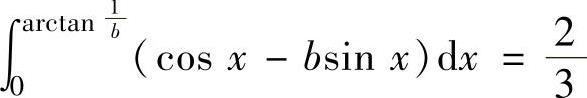 ,即
,即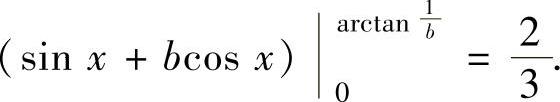
由此得到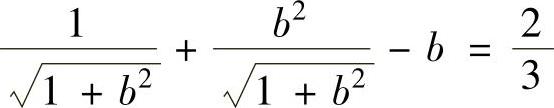 ,即
,即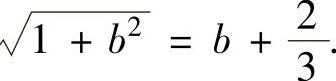
解此方程得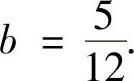
相关文章

如果圆锥的母线长为l,底面半径为r,那么圆锥侧面展开的扇形半径为________,扇形的弧长为________,圆锥的侧面积为________,圆锥的全面积为_________.1.若将半径为24cm的半圆形纸片围成一个圆锥的侧面,则这个圆锥的底面圆半径为( ).A.3cm B.6cm C.12cm D.24cm2.已知圆锥底面圆的半径为6m,它的侧面积为60πcm2,则这个圆锥的高是( ).A.......
2025-09-29

把一个平面图形绕着平面内某一点O旋转一个角度,叫做图形的_________,点O叫做________,转动的角叫做________.旋转的性质:对应点到旋转中心的距离________.对应点与旋转中心所连线段的夹角等于_________.旋转前、后的图形________.1.下列现象:①时针的转动;②摩天轮的转动;③地下水位逐年下降;④传送带上的机器人.其中属于旋转的是( ).A.①② B.②③......
2025-09-29

当第1、第3段均为圆弧时,CNC可自动显示图6.3-9c所示的全部可能的圆弧轨迹,供操作者选择,选定后,第2圆弧段随即确定,第3程序段成为终点不定的未决程序段。图6.3-10 不相交线的相切圆弧......
2025-09-29

常规的NC加工程序必须通过计算确定程序段终点,但采用轮廓编程可同时对多个程序段的轨迹进行编程,由CNC自动计算各程序段的终点坐标。FS-0iD最大允许存在连续10个未决程序段,根据不同的轮廓,未决程序段的处理按以下规则进行。......
2025-09-29

请说明理由.若矩形ABCD面积为6,求四边形BDEG的面积.(第9题)10.在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称……......
2025-09-29

璀璨的星空令人无限神往,哥白尼曾说:“有什么东西能比天空更美好呢?要知道天空囊括了一切美好的东西.”左图是埃舍尔创作的《星空》,他对多面体和框架星体情有独钟,主体框架星体里住着两条变色龙,给宇宙星空增添了生气和趣意.知能概述图形有具体的,有抽象的;有平面的,有立体的.它既可以是艺术中的绘画和雕塑,也可以是科学上的表达或记录.立体图形与平面图形之间的联系体现在以下方面:立体图形的展开与折叠,从不同方......
2025-09-29

两平面立体相交,其相贯线在一般情况下是封闭的空间折线,但有时也会是平面多边形。从图4-17中可以看出,相贯线(折线)上任一段直线都是甲平面立体的一个棱面与乙立体的一个棱面的交线。因此,求作两平面立体相贯线,实质上仍归结为求直线与平面的交点,以及求平面与平面交线的问题。求直立三棱柱与水平三棱柱的相贯线,如图4-17所示。......
2025-09-29

本范例要完成的计算机网络图形符号如图8-13所示,它用于标识计算机网络本身或指示计算机网络的连接终端。下面介绍如何绘制该计算机网格图形符号。图8-13 计算机网格图形符号图8-13 计算机网格图形符号系统默认的当前图层为“0”层,此时可以更改默认线宽。再绘制其他3条直线段,绘制方法如下。单击“矩形”按钮,在图形窗口中绘制一个长为6、宽为3.5的长方形(矩形)。......
2025-09-29
相关推荐