讨论合力对某点的矩和分力对该点的矩的关系,就是我们下面要讲述的合力矩定理。图3-17力矩投影由图3-17 可以看出将上述等式两边相加,有根据合力投影定理,有于是定理得到证明。对于有合力的其他各种力系,合力矩定理也是成立的。求啮合力Fn 对轮心点O 的矩。......
2025-09-29
【主要内容】
1.积分中值定理
设函数f(x)在[a,b]上连续,则存在ξ∈[a,b],使得
注 (ⅰ)当上述的f(x)是单调函数时,中值ξ∈(a,b).
(ⅱ)积分中值定理具有以下的推广形式:
设函数f(x)在[a,b]上连续,函数g(x)在[a,b]上可积且不变号,则存在ξ∈[a,b],使得
2.积分中值定理的应用
积分中值定理主要用于把抽象函数f(x)的定积分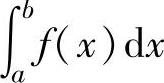 转换成f(x)在[a,b]上某点
转换成f(x)在[a,b]上某点
η处的值与(b-a)之积,即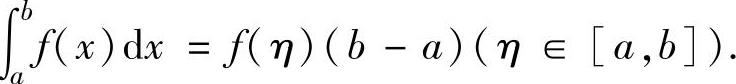 这样可以减少积分运算,
这样可以减少积分运算,
使问题的计算或证明变得简单些.
【典型例题】
例2.8.1 设函数f(x)在(-∞,+∞)上有连续导数,求极限
精解 先应用积分中值定理去掉积分运算.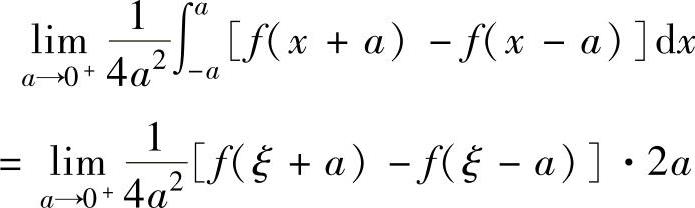 (对f(x+a)-f(x-a)在[-a,a]上应用积分中值定理,其中ξ∈[-a,a])
(对f(x+a)-f(x-a)在[-a,a]上应用积分中值定理,其中ξ∈[-a,a])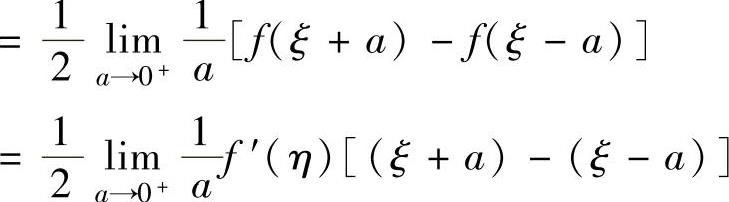 (对f(x)在[ξ-a,ξ+a]上应用拉格朗日中值定理,其中η∈(ξ-a,ξ+a))
(对f(x)在[ξ-a,ξ+a]上应用拉格朗日中值定理,其中η∈(ξ-a,ξ+a))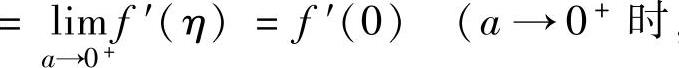 ,ξ→0,从而η→0).
,ξ→0,从而η→0).
例2.8.2 设函数f(x)在[0,1]上可导,且满足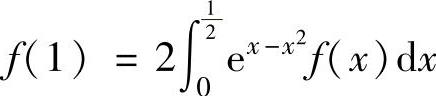 ,证明:存在ξ∈
,证明:存在ξ∈
(0,1),使得f′(ξ)=(2ξ-1)f(ξ).
精解 本题需作辅助函数,为此将欲证等式中的ξ改为x得
f′(x)=(2x-1)f(x), 即 ex-x2f′(x)+ex-x2(1-2x)f(x)=0.由此得到[ex-x2f(x)]′=0.故作辅助函数(https://www.chuimin.cn)
F(x)=ex-x2f(x),
则F(x)在[0,1]上可导,且由题设及积分中值定理有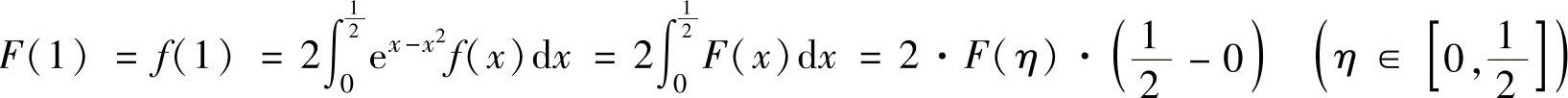 ,
,
即F(1)=F(η).所以,对F(x)在[η,1]上应用罗尔定理知,存在ξ∈(η,1)⊂(0,1),使得
F′(ξ)=0, 即 f′(ξ)=(2ξ-1)f(ξ).
例2.8.3 设函数f(x)在[0,2]上连续,在(0,2)内二阶可导且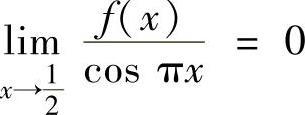 ,
,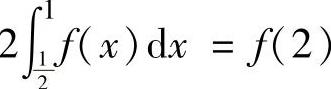 .证明:存在ξ∈(0,2),使得f″(ξ)=0.
.证明:存在ξ∈(0,2),使得f″(ξ)=0.
精解 由于f(x)在[0,2]上连续,在(0,2)内二阶可导,所以只要在[0,2]上找到不同的两点,使得在这两点处f′(x)的值相等即可,具体证明如下.由题设知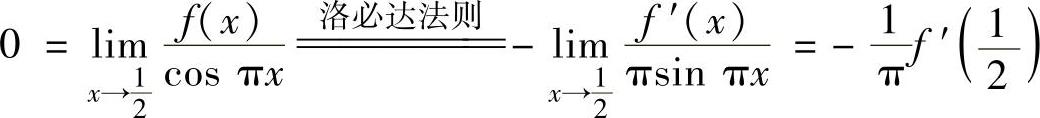 ,即
,即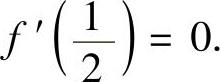
另由题设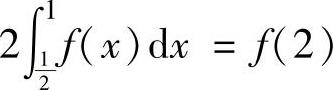 及积分中值定理知,存在
及积分中值定理知,存在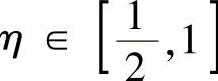 ,使得f(η)=f(2).
,使得f(η)=f(2).
于是,对f(x)在[η,2]上应用罗尔定理知,存在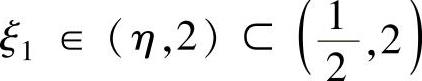 ,使得f′(ξ1)=0.
,使得f′(ξ1)=0.
由此可知,f′(x)在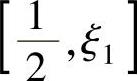 上满足罗尔定理条件,从而存在
上满足罗尔定理条件,从而存在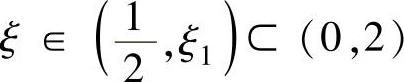 ,使得f″(ξ)=0.
,使得f″(ξ)=0.
例2.8.4 设函数f(x)在[0,1]上连续,且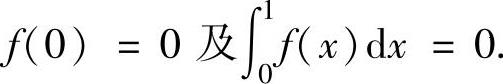 证明:存在ξ∈
证明:存在ξ∈
(0,1),使得∫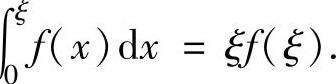
精解 本题需作辅助函数,为此将欲证等式中的ξ改为x得
当x∈(0,1)时,上式可改写成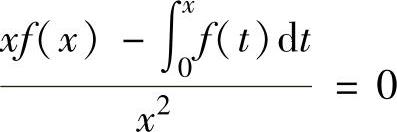 ,即
,即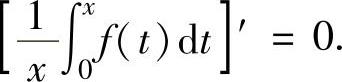
因此作辅助函数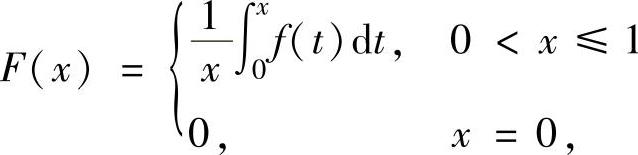 ,则F(x)在[0,1]上连续,在(0,1)内可
,则F(x)在[0,1]上连续,在(0,1)内可
导,且F(0)=F(1)=0,即F(x)在[0,1]上满足罗尔定理条件,所以存在ξ∈(0,1),使得F′(ξ)=0,即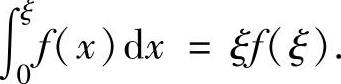
相关文章

讨论合力对某点的矩和分力对该点的矩的关系,就是我们下面要讲述的合力矩定理。图3-17力矩投影由图3-17 可以看出将上述等式两边相加,有根据合力投影定理,有于是定理得到证明。对于有合力的其他各种力系,合力矩定理也是成立的。求啮合力Fn 对轮心点O 的矩。......
2025-09-29

应该指出,式中,没有对牵连运动作任何限制,因此,速度合成定理对于任何形式的牵连运动都适用。因此,动点在某一瞬时的牵连速度和加速度,实际上是动坐标系上与动点相重合的那一点,即牵连点的速度和加速度。应用速度合成定理:式中ve,vr——分速度;va——合速度。由图中的几何关系,求得绝对速度的大小为......
2025-09-29

合力矩定理是力学中应用十分广泛的一个重要定理,现用两个汇交力系的情形给以证明。为此,根据合力矩定理,合力R对A点的矩等于F1、F2对A点的矩的代数和。根据合力矩定理可知,分布荷载对某点的矩就等于其合力对该点的矩。......
2025-09-29

下面将给出几个关于第(1)类非扩张映象在Hilbert 空间上的定义和定理.定理1(Browder-Petryshyn)设H 是一个Hilbert 空间,C 为Hilbert 空间H 的非空有界闭凸子集.设T∶C→C 使第(1)类非扩张型映象,则T 在C中存在不动点.通常用F(T)来表示T 的不动点集,即F(T)={x ∈C∶Tx=x}.定理2(Browder)设X 是一致凸Banach 空间......
2025-09-30

【主要内容】1.罗尔定理设函数f(x)在[a,b]上连续,在(a,b)内可导,且f(a)=f(b),则存在ξ∈(a,b),使得f′(ξ)=0.罗尔定理有各种推广形式,例如(1)设函数f(x)在(a,b)内可导,且与存在且相等,则存在ξ∈(a,b),使得f′(ξ)=0.(2)设函数f(x)在[a,+∞)上连续,在(a,+∞)上可导,且,则存在ξ∈(a,+∞),使得f′(ξ)=0.2.罗尔定理应用方法......
2025-09-30

纵联方向保护有独立的方向元件;既可以使用载波通道也可以使用光纤通道;也能构成“闭锁式”保护和构成“允许式”保护。“闭锁式”纵联方向保护起动后若判故障为反向故障,发出闭锁信号;反之则停止发信号。闭锁式保护原理如图4-19所示。图7-28 McSBP例程实验结果......
2025-09-29

上面方程式中的Mu和Mi与所需变换的坐标系相关,因此,该变换矩阵并不是唯一的。如果将式和式代入式可得IU==I′MiMuU′ 从上式可看出,当满足功率不变约束时,必须有下式成立:MiMu=1或者Mi=Mu-1 2.电压和电流具有同一变换系数矩阵的变换采用功率不变约束的变换,虽然能使变换成为唯一,但是其电压变换系数矩阵和电流变换系数矩阵可能并不相同。......
2025-09-29

销主要用来固定零件之间的相对位置,称为定位销 ,它是组合加工和装配时的重要辅助零件;也可用于连接,称为连接销 ,可传递不大的载荷;还可作为安全装置中的过载剪断元件,称为安全销 。图3-8定位销图3-9连接销图3-10安全销销有多种类型,如圆柱销、圆锥销、槽销等,这些销均已标准化。定位销通常不受载荷,故不作强度校核计算,其直径可按结构确定,数目一般不少于两个。......
2025-09-29
相关推荐