首页理论教育积分上限函数的求导方法：六种有效策略

积分上限函数的求导方法：六种有效策略

2025-09-30 理论教育版权反馈

【摘要】：【主要内容】设f（x）是连续函数，则积分上限函数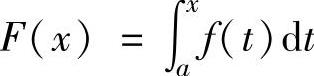可导且F′（x）=f（x），即由此可知，是f（x）的一个原函数，即注（ⅰ）设f（u）是连续函数，u（x）是可导函数，且f（u）与u=u（x）可复合成复合函数f（u（x）），则（ⅱ）计算函数（注意：被积函数f（t，x）中除积分变量t外还含有与积分上限相同的x）的导数时，应先将x从被积函数f（t，x）中移走（即移到积分号之外，或移到积分限中去），然后

【主要内容】

设f（x）是连续函数，则积分上限函数可导且F′（x）=f（x），即

由此可知，是f（x）的一个原函数，即

注（ⅰ）设f（u）是连续函数，u（x）是可导函数，且f（u）与u=u（x）可复合成复合函数f（u（x）），则

（ⅱ）计算函数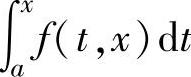（注意：被积函数f（t，x）中除积分变量t外还含有与积分上限相同的x）的导数时，应先将x从被积函数f（t，x）中移走（即移到积分号之外，或移到积分限中去），然后再计算导数.

【典型例题】

例2.6.1 已知f（x）是连续函数，且满足，求f（x）的表达式.

精解所给等式两边对x求导得

其中，计算时应将先将x移到积分号之外，即

此外，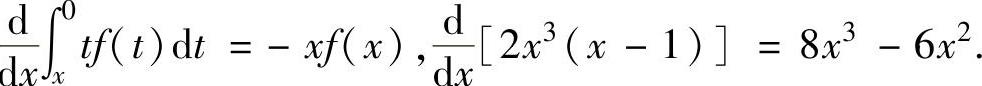

将它们代入式（1）得，

化简后得

上式两边对x求导得f（x）·2=24x²-12x，即 f（x）=12x²-6x.

例2.6.2 设函数，求定积分

精解用分部积分法计算所给的定积分.

例2.6.3 （单项选择题）把x→0+时的无穷小，β，排列起来，使排在后面的是前面的一个高阶无穷小，则正确的排列次序为（）.

A.α，β，γ B.α，γ，β

C.β，α，γ D.β，γ，α

精解只要算出当x→0+时，α，β，γ关于x的阶数即可.

由于，，，

所以，当x→0^+时，α，β，γ分别是x的1阶、3阶与2阶无穷小，所以正确排列为α，γ，β.因此本题选B.(https://www.chuimin.cn)

例2.6.4 设函数f（x），求极限_xl→im₀f（x）.

精解先算出，然后用洛必达法则计算.由于，所以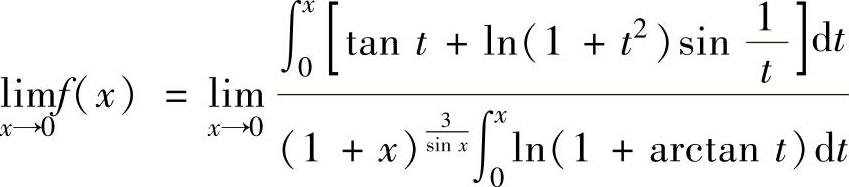

（由于x→0时，ln（1+arctanx）～arctanx～x）

注在计算型未定式极限时，如果经化简后分子或分母中有积分上限函数，则应使用洛必达法则去掉积分运算，然后再计算极限，本题就是这样处理的.

例2.6.5 设函数f（x）连续，且f（0）=0，f′（0）=0.记求F′（x）和F″（0）.

精解先由积分上限函数求导方法算出x<0和x>0时的F′（x），然后由导数定义计算F′（0）及F″（0）.

当x<0时，

当x>0时，由得

此外，由，

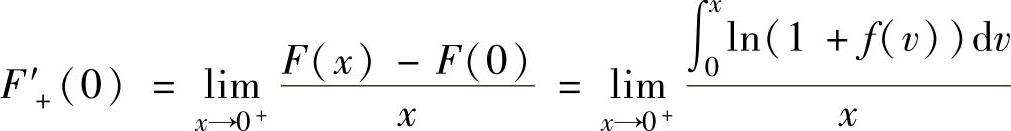
知F′（0）=0.从而

利用上述的F′（x）表达式得

所以，F″（0）=0.

例2.6.6 设函数，求它的值域.

精解由于|sint|是以π为周期的周期函数，所以容易证明f（x）也是以π为周期的周期函数.于是只要算出连续函数f（x）在[0，π]上的最小值m和最大值M，即得f（x）的值域为[m，M].

对任意x∈（-∞，+∞）有（利用|sinu|是以π为周期的周期函数）=f（x）

即f（x）是以π为周期的周期函数，由

知在（0，π）内的可能极值点（即驻点）为，由于f（x）在[0，π]上连续，且，，

f（π）=f（0）=1.

所以，f（x）在[0，π]上，即在（-∞，+∞）上的最小值、最大值分别为

从而f（x）的值域为