首页理论教育数学考研基础篇：奇偶函数和周期函数的定积分性质及重要公式

数学考研基础篇：奇偶函数和周期函数的定积分性质及重要公式

2025-09-30 理论教育版权反馈

【摘要】：1.奇、偶函数的定积分性质设f在对称区间[-a，a]（a>0）上连续.如果它是奇函数（偶函数），则注（ⅰ）当f是非奇非偶的连续函数时，由于所以有（ⅱ）当[a，b]不是对称区间时，可令a+b，将[a，b]转换成对称区间2.周期函数的定积分性质设函数f在上连续，且是周期为T（T>0）的周期函数，则对任意实数a和正整数n有3.重要公式对n=2，3，…

【主要内容】

1.奇、偶函数的定积分性质设f（x）在对称区间[-a，a]（a>0）上连续.如果它是奇函数（偶函数），则

注（ⅰ）当f（x）是非奇非偶的连续函数时，由于所以有

（ⅱ）当[a，b]不是对称区间时，可令

a+b（注意₂是[a，b]的中点），将[a，b]

转换成对称区间

2.周期函数的定积分性质

设函数f（x）在（-∞，+∞）上连续，且是周期为T（T>0）的周期函数，则对任意实数a和正整数n有

3.重要公式

对n=2，3，…有n是大于1的奇数，，n是偶数.

【典型例题】

例2.5.1 求定积分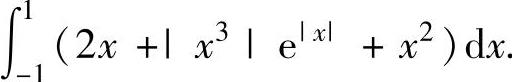

精解由于积分区间是对称区间，所以利用奇、偶函数的定积分性质计算.

例2.5.2 求定积分

精解由于积分区间为对称区间，所以利用奇、偶函数的定积分性质计算本题.

其中，（奇函数在对称区间上的定积分为零），（偶函数在对称区间上的定积分）

将它们代入式（1）得(https://www.chuimin.cn)

例2.5.3 求定积分

精解积分区间[0，π]不是对称区间，故令，则

例2.5.4 求定积分

精解被积函数虽然是非奇非偶函数，但可以表示成

所以

例2.5.5 设f（x）是以2为周期的周期函数，且在[-1，1]上

精解由于f（x）是以2为周期的周期函数，且在[-1，1]上是奇函数，所以f（x）sinπx是以2为周期的周期函数，且它在[-1，1]上是偶函数，因此利用周期函数的定积分性质和偶函数的定积分性质有

其中，，

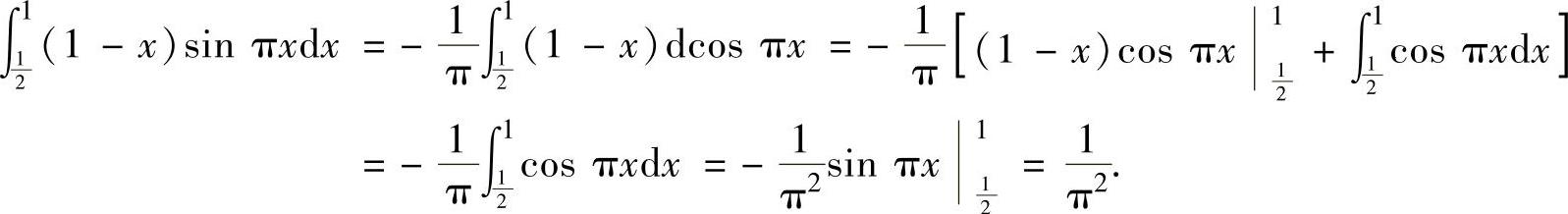
将它们代入式（1）得

例2.5.6 求定积分

精解

其中，（由于sin¹⁰x·cos⁸x是以π为周期的周期函

数）

（由于sin⁸u是以π为周期的周期函数）

（由于sinx·sin2x·sin4x是以2π为周期的奇函数）将它们代入式（1）得