首页理论教育定积分概念与计算方法

定积分概念与计算方法

2025-09-30 理论教育版权反馈

【摘要】：，Δxn，并在每个小区间上任取一点ξ1，ξ2，…

【主要内容】

1.定积分的概念

设函数f（x）在[a，b]上有界，在[a，b]上任意插入n-1个分点

a=x₀<x₁<x₂<…<x_n-1<x_n=b，把[a，b]分成n个小区间

[x₀，x1]，[x₁，x2]，…，[x_n-1，xn]，

它们的长度对应地记为Δx₁，Δx₂，…，Δx_n，并在每个小区间上任取一点ξ₁，ξ₂，…，ξ_n.若无论上述x₁，…，x_n和ξ₁，…，ξn如何取，极限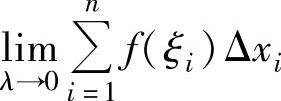（其中，λ=max{Δx₁，Δx₂，…，Δx_n}）

总是存在且相等，则称f（x）在[a，b]上可积，称这个极限值为f（x）在[a，b]上的定积分，记为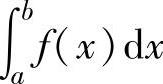，并定义：

当a>b时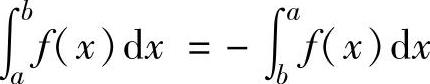，；当a=b时，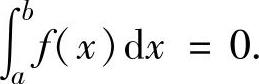

注（ⅰ）f（x）在[a，b]上可积的充分条件

当函数f（x）在[a，b]上连续，或在[a，b]上只有有限个第一类间断点，或在[a，b]上单调有界时，f（x）在[a，b]上可积.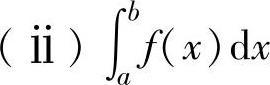的几何意义

如果f（x）在[a，b]上为非负函数，则当它可积时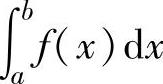，表示由曲线y=f（x），直线x=

a，x=b以及x轴围成的曲边梯形的面积.

例如，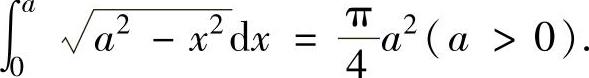

2.定积分的计算方法

定积分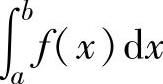的计算可按牛顿-莱布尼茨公式、定积分性质和换元积分法、分部积分法进行.

（1）牛顿-莱布尼茨公式

设函数f（x）在[a，b]上连续，F（x）是f（x）的一个原函数，则

（2）定积分性质

设f（x），g（x）都是[a，b]上的可积函数，k为常数，则

（3）换元积分法

换元积分法：设函数f（x）在[a，b]上连续，函数x=φ（t）满足：

1）φ（α）=a，φ（β）=b；

2）φ（t）在[α，β]（或[β，α]）上有连续的导数；

3）当t从α连续变化到β时，φ（t）从a连续变化到b，则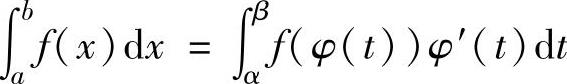或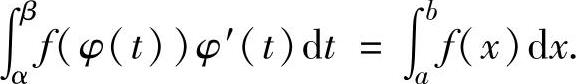

（4）分部积分法

设函数u（x），v（x）在[a，b]上有连续的导数，则(https://www.chuimin.cn)

【典型例题】

例2.4.1 求定积分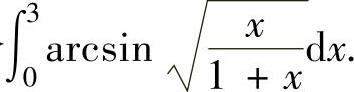

精解由于被积函数很复杂，故将其代换为t，即令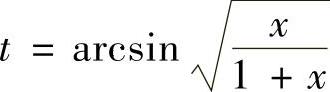，则x=tan²t.于是

例2.4.2 求定积分∫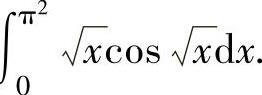

精解先作变量代换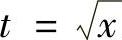，再用分部积分法计算.，

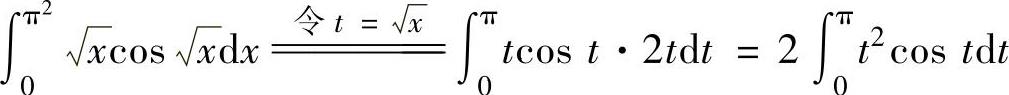取u（t）=t²，则由dv（t）=costdt=dsint得v（t）=sint，所以，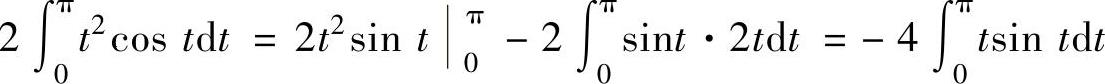

取u₁（t）=t，则由dv₁（t）=sintdt=d（-cost）得v₁（t）=-cost，所以

由此得到

注本题的计算过程可以写得紧凑一些，具体如下：

例2.4.3 求定积分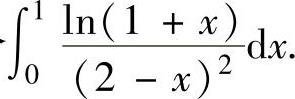

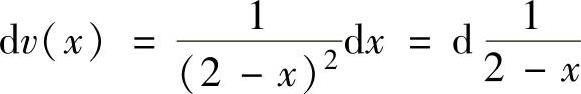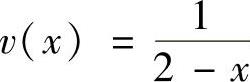精解用分部积分法计算所给的定积分，其中，取u（x）=ln（1+x），则由得，所以

例2.4.4 设函数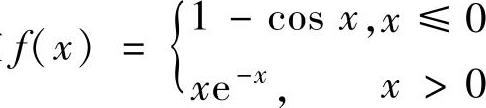，，求∫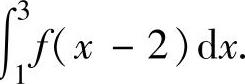

精解根据f（x）的定义，应先作变量代换t=x-2，然后计算定积分.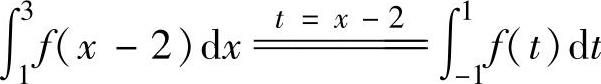

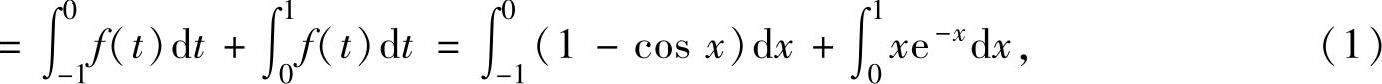
其中，，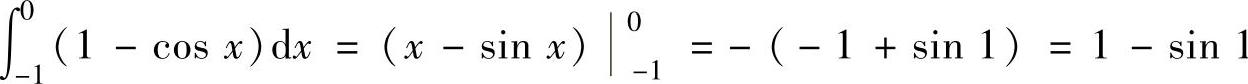

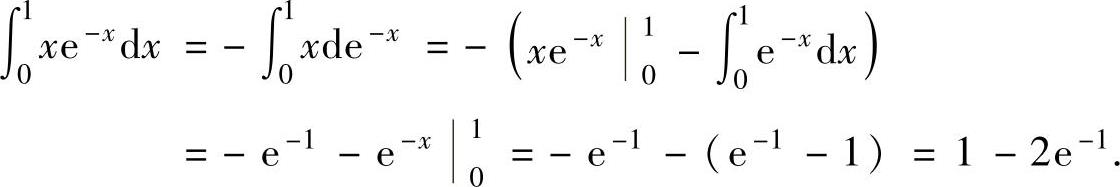
将它们代入式（1）得

例2.4.5 设函数f（x）在（-∞，+∞）上满足f（x）=f（x-π）+sinx，且f（x）=x，x∈[0，π），求定积分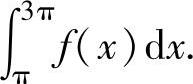

精解先按题设写出f（x）在[π，3π]上的分段表达式，然后计算所给的定积分.由题设知，x∈[π，2π）时，f（x）=f（x-π）+sinx=（x-π）+sinx=x-π+sinx，x∈[2π，3π）时，f（x）=f（x-π）+sinx=[（x-π）-π+sin（x-π）]+sinx=x-2π，此外，f（3π）=f（3π-π）+sin3π=f（2π）=2π-2π=0，

所以，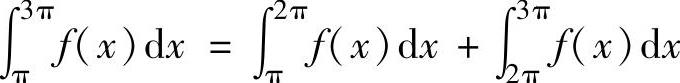

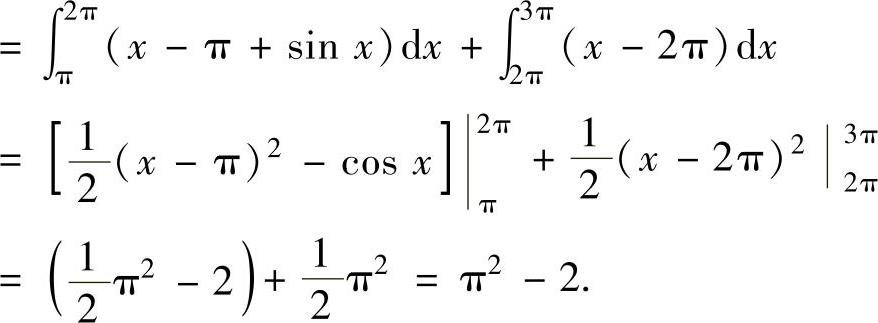
例2.4.6 设连续函数f（x）满足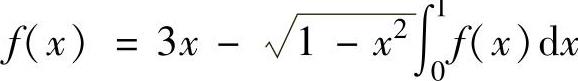，求f（x）的表达式.

精解由于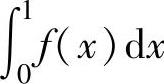是常数，记其为A，则f（x）满足的等式变为

式（1）两边从0到1积分得

其中，，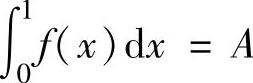

（这里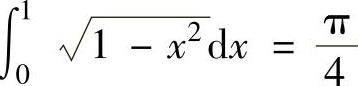是利用定积分的几何意义得到的）.

将它们代入式（2）得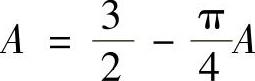，即，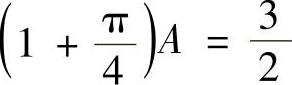

所以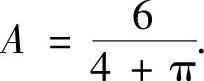，将它代入式（1）得