【主要内容】计算函数的导数的基础是求导基本公式和四则运算法则.求导基本公式:(1)C′=0(C是常数),(2)(xμ)′=μxμ-1,(3)(ax)′=axlna(常数a>0但a≠1),特别地,(ex)′=ex,(4),特别地,,(5)(sinx)′=cosx, (6)(cosx)′=-sinx,(7)(tanx)′=sec2x, (8)(cotx)′=-csc2x,(9)(secx)′=secx......
2025-09-30
【主要内容】
1.有理函数不定积分的计算方法
设P(x),Q(x)分别是m,n(m,n都是自然数)次多项式,且它们是不可约的,则称∫PQ((xx))dx为有理函数的不定积分.
当m≥n时,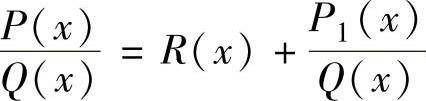 ,其中,R(x)是m-n次多项式,P1(x)是r(r<n)次
,其中,R(x)是m-n次多项式,P1(x)是r(r<n)次
多项式.因此有理函数的不定积分主要考虑计算m<n时的不定积分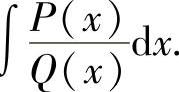 它的计算方
它的计算方
法如下:
先将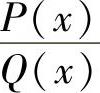 分成部分分式.
分成部分分式.
当Q(x)有因子(x-a)k(k为正整数,且k≤n)时,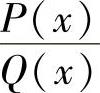 的部分分式中,有形如
的部分分式中,有形如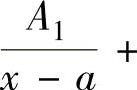
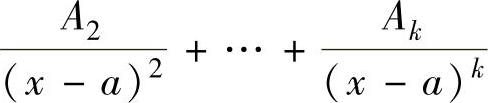 的和项;
的和项;
当Q(x)有因子(x2+px+q)k(k为正整数,且2k≤n以及p2-4q<0)时,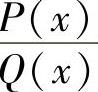 的部分
的部分
分式中,有形如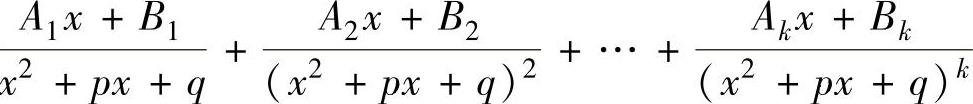 的和项.
的和项.
然后,对P(x)
Q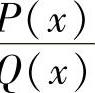 的部分分式的各项积分相加,由此算出不定积分
的部分分式的各项积分相加,由此算出不定积分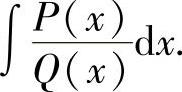
但是,有理函数不定积分的计算,不能拘泥于分部分分式的方法,它应与换元积分法或分部积分法相结合,才能化简整个不定积分计算过程.
2.三角函数有理式、简单无理函数不定积分的计算方法
(1)设R(u,v)是变量u,v的有理式(即由u,v和常数经过有限次四则运算构成的表达式),则称R(sinx,cosx)为三角函数有理式,称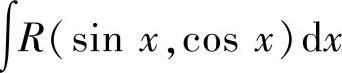 为三角函数有理式的不定
为三角函数有理式的不定
积分,它可由变量代换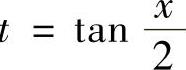 转换成关于t的有理函数的不定积分进行计算.但是使用以
转换成关于t的有理函数的不定积分进行计算.但是使用以
下结论往往会使计算更加快捷:
(ⅰ)如果R(-u,v)=-R(u,v)(即R关于u是奇函数),则令t=cosx;
(ⅱ)如果R(u,-v)=-R(u,v)(即R关于v是奇函数),则令t=sinx;
(ⅲ)如果R(-u,-v)=R(u,v),则令t=tanx.
(2)设R1(u,v)和R2(u,v)都是变量u,v的有理式,则简单无理函数是指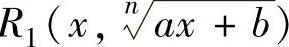 和
和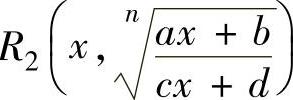 ,其中,n是大于1的整数,a,b,c,d都为常数,且a≠0,c≠0,ad-bc≠0.
,其中,n是大于1的整数,a,b,c,d都为常数,且a≠0,c≠0,ad-bc≠0.
简单无理函数∫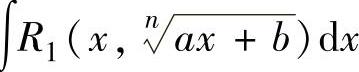 和
和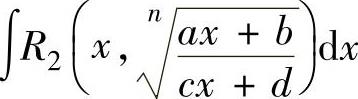 可分别由代换
可分别由代换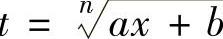 和
和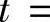
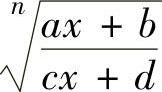 转换成关于t的有理函数的不定积分进行计算.
转换成关于t的有理函数的不定积分进行计算.
【典型例题】
例2.3.1 求不定积分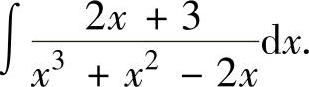
精解 所给的不定积分是有理函数的不定积分,所以先将被积函数分成部分分式.由于x3+x2-2x=x(x2+x-2)=x(x-1)(x+2),
所以,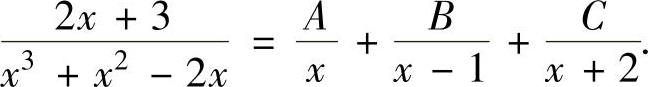 由此可得
由此可得
2x+3=A(x-1)(x+2)+Bx(x+2)+Cx(x-1)(https://www.chuimin.cn)
=A(x2+x-2)+B(x2+2x)+C(x2-x)
=(A+B+C)x2+(A+2B-C)x-2A.
比较上式两边关于x的同次幂系数得方程组
解此方程组得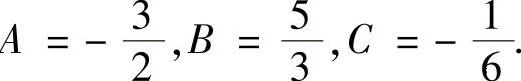 所以
所以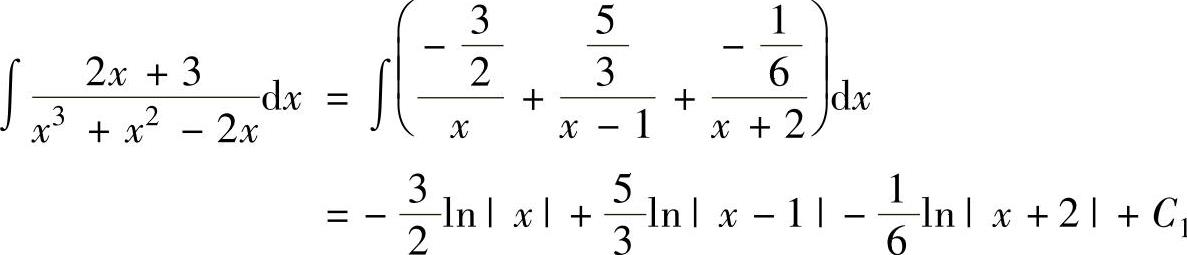 (其中C1为常数).
(其中C1为常数).
例2.3.2 求不定积分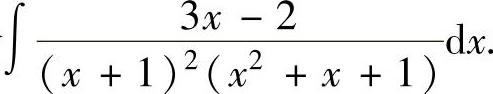
精解 所给的不定积分是有理函数的不定积分,但分母的次数较高,如直接采用分部积分法计算,将是比较复杂的.故先作变量代换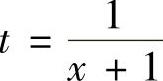 ,将分母中的(x+1)2因子移走,然后再
,将分母中的(x+1)2因子移走,然后再
计算不定积分.
例2.3.3 求不定积分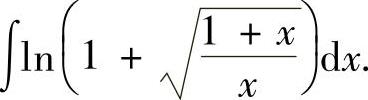
精解 由于被积函数中包含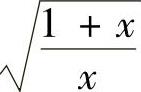 ,所以先作变量代换
,所以先作变量代换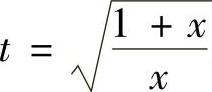 ,并应用分部积分法,
,并应用分部积分法,
把所给不定积分转换成有理函数的不定积分.
其中,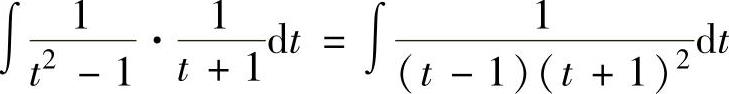 是有理函数的不定积分,因此将被积函数分成部
是有理函数的不定积分,因此将被积函数分成部
分分式:
即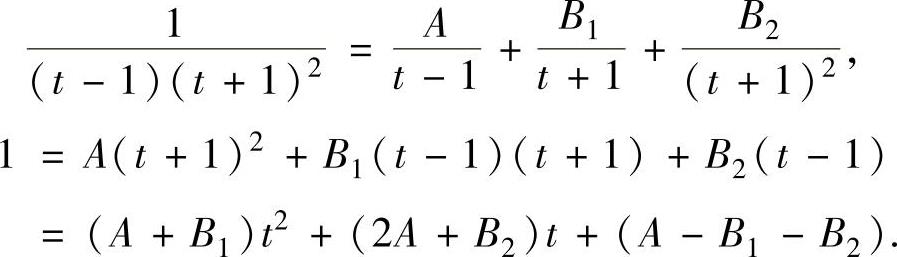
比较上式两边关于t的同次幂系数得
解此方程组得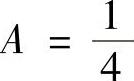 ,B
,B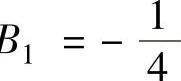 ,B
,B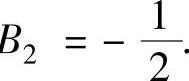 所以,
所以,
将式(2)代入式(1)得
注 本题的被积函数比较复杂,它含有无理函数和对数函数,因此需应用换元积分法和分部积分法,把结果转换成计算有理函数的不定积分,这也是常用的计算不定积分的方法.
例2.3.4 求不定积分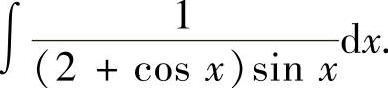
精解 所给的不定积分是三角函数有理式的不定积分(其中,有理式为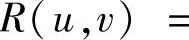
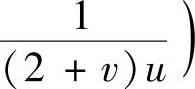 ,因此可以用变量代换
,因此可以用变量代换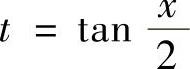 将这个不定积分转换成有理函数的不定积分.但
将这个不定积分转换成有理函数的不定积分.但
是注意到R(-u,v)=-R(u,v),故令t=cosx,将会使计算更简单些.
对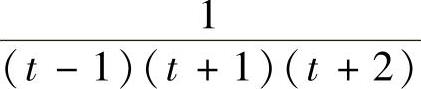 分部分式:
分部分式:
即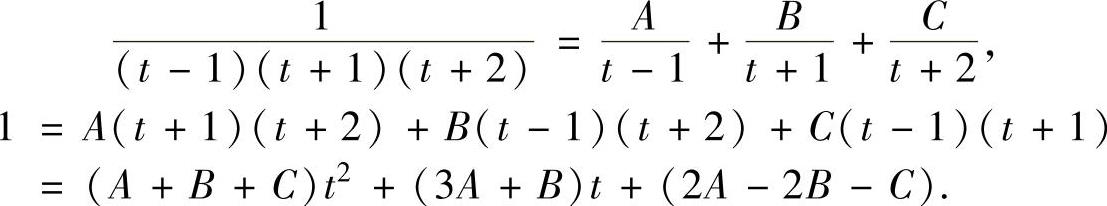
比较上式两边关于t的同次幂系数得
解此方程组得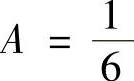 ,
,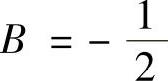 ,
,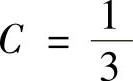 ,所以
,所以
(其中C1为常数)(2)将式(2)代入式(1)得
相关文章

【主要内容】计算函数的导数的基础是求导基本公式和四则运算法则.求导基本公式:(1)C′=0(C是常数),(2)(xμ)′=μxμ-1,(3)(ax)′=axlna(常数a>0但a≠1),特别地,(ex)′=ex,(4),特别地,,(5)(sinx)′=cosx, (6)(cosx)′=-sinx,(7)(tanx)′=sec2x, (8)(cotx)′=-csc2x,(9)(secx)′=secx......
2025-09-30

知识要点一、原函数与不定积分概念1.概念:原函数是积分学中的一个重要概念,求不定积分就是求被积函数的全体原函数,要在理解原函数概念的基础上,弄清不定积分与微分之间的内在关系,能根据积分与微分的互逆关系求不定积分.2.不定积分的性质:3.不定积分的法则与公式:公式要熟练掌握.二、直接积分法直接利用不定积分的公式和性质求函数不定积分.三、第一类换元积分法(凑微分法)设f(u)有原函数F(u),u=φ(......
2025-09-30

图8-14 RC滤波电路在C1=4000μF,T=0.02s条件下,电容C1的脉动系数S1为又根据RC滤波电路输出负载上的脉动系数S的计算公式(8-6)可直接求得负载RL上的脉动系数S的值。推导电路输出负载RL上的直流平均电压UO和脉动系数S的计算公式。......
2025-09-29

试述调和函数的定义、特性及应用。调和函数的意义。调和函数的特性。工程数学或高等数学发现,如果一个函数u(x,y)为调和函数,则该函数具备“可迭加”的特性。证明如果流体为x-y平面理想流体,流体在流动时的流线函数φ为调和函数,则函数具有迭加性。......
2025-09-29

在线性校准中,校准直线函数相关估计值的获得是使用或评价校准直线的基础。式中,Sxy=-[(∑xn)(∑yn) /N]式中, 校准直线函数相关参数的估计与计算采用高效液相色谱法对甲醛系列标准工作溶液进行检测,甲醛系列标准工作溶液仪器响应示值结果如表2-1所示,估计校准直线的函数及其相关参数。......
2025-09-29

续表考点1:函数1.(2017全国I,5)函数f(x)在(-∞,+∞)上单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是().A.[-2,2]B.[-1,1]C.[0,4]D.[1,3]考点2:对数函数2.(2017全国I,11)设x,y,z为正数,且2x=3y=5z,则().A.2x<3y<5zB.5z<2x<3yC.3y<5z<2xD......
2025-09-30

【主要内容】设f′(x)>0(x∈(a,b))或f′(x)≥0(x∈(a,b),但仅在有限个点处取等号),则函数f(x)在(a,b)内单调增加;设f′(x)<0(x∈(a,b))或f′(x)≤0(x∈(a,b),但仅在有限个点处取等号),则函数f(x)在(a,b)内单调减少.注 (ⅰ)以上结论在a=-∞或b=+∞时仍成立;(ⅱ)当f(x)在[a,b]上连续时,端点x=a,x=b可以并入到f(x)的......
2025-09-30

所谓出版产品需求函数,是指在某一特定时期内,某种出版产品的各种可能的需求量和决定这些需求量的因素之间的关系。出版产品需求函数表示的是出版产品的市场需求量Qd的大小是由出版产品价格、消费者收入、广告宣传费、出版替代品价格决定的。现以某杂志的需求函数为例,来说明出版产品需求函数的应用。......
2025-09-29
相关推荐