知识要点一、原函数与不定积分概念1.概念:原函数是积分学中的一个重要概念,求不定积分就是求被积函数的全体原函数,要在理解原函数概念的基础上,弄清不定积分与微分之间的内在关系,能根据积分与微分的互逆关系求不定积分.2.不定积分的性质:3.不定积分的法则与公式:公式要熟练掌握.二、直接积分法直接利用不定积分的公式和性质求函数不定积分.三、第一类换元积分法(凑微分法)设f(u)有原函数F(u),u=φ(......
2023-10-26
【主要内容】
1.不定积分的概念
函数f(x)在区间I上的原函数全体F(x)+C(其中,F(x)是f(x)的一个原函数,即F′(x)=f(x),C是任意常数),称为f(x)的不定积分,记为∫f(x)dx.
不定积分的计算主要依靠不定积分的基本公式、基本性质及基本运算方法.
基本公式
(1) ,
,
(2)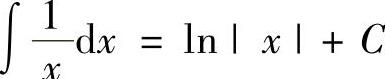 ,
,
(3) ,
,
(4) ,
,
(5) ,
,
(6) ,
,
(7)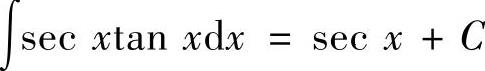 ,
,
(8)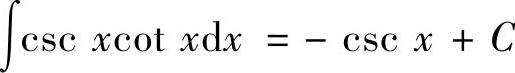 ,
,
(9)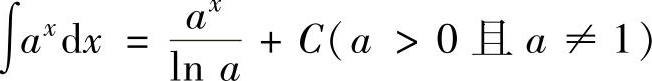 ,特别地,
,特别地,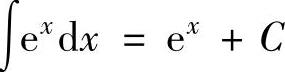 ,
,
(10) ,
,
(11)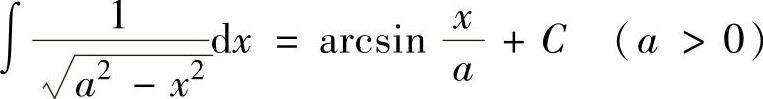 ,
,
(12)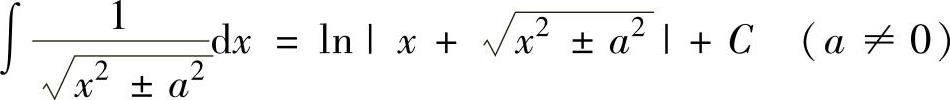 ,
,
此外,还有
(13) ,
,
(14)
(15)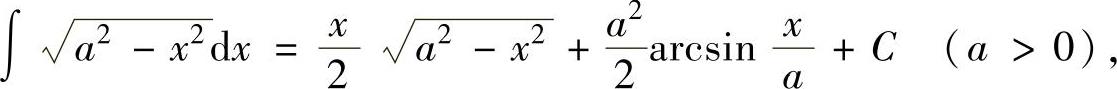
(16)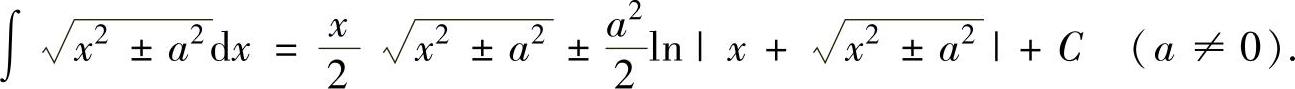
基本性质
设函数f(x),g(x)的原函数存在,k为常数,则
(1)
(2)
(3)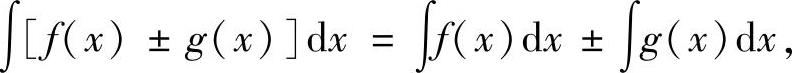
(4)
基本运算方法
(1)换元积分法;
(2)分部积分法(放到下一节讲).
2.不定积分的换元积分法
换元积分法就是通过适当的变量代换(简称换元),将要求的不定积分转换成基本公式中的不定积分,从而算出要求的不定积分,即
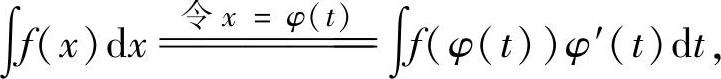
或者
如果以上两式中右边的不定积分都是基本公式中的不定积分,则由此算出左边要求的不定积分.
注 用换元积分法计算不定积分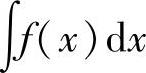 时,采用什么样的变量代换,应视具体情况而(www.chuimin.cn)
时,采用什么样的变量代换,应视具体情况而(www.chuimin.cn)
定,但以下两点值得注意:
(ⅰ)如果f(x)是一个分式,而分母比较复杂,为去掉分母中的某些因子,或将分母中的某些因子移到分子中去,使分母变得简单些,可使用变量代换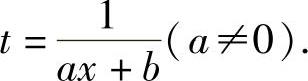
(ⅱ)如果f(x)中含有根式,则作变量代换将根式去掉,例如,
当f(x)中含有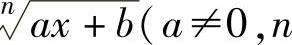 是大于1的正整数)时,可令
是大于1的正整数)时,可令
当f(x)中含有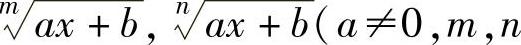 都是大于1的正整数)时,可令
都是大于1的正整数)时,可令 ,其
,其
中,k是m,n的最小公倍数;
当f(x)中含有 (其中a,c都不为零,且ad≠bc,n是大于1的正整数)时,可令
(其中a,c都不为零,且ad≠bc,n是大于1的正整数)时,可令
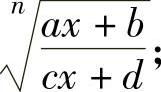
当f(x)中含有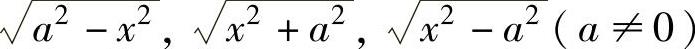 时,分别令x=asint,x=atant,x=asect.
时,分别令x=asint,x=atant,x=asect.
【典型例题】
例2.1.1 求不定积分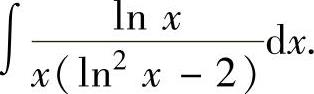
精解 由于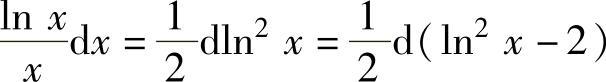 ,所以
,所以
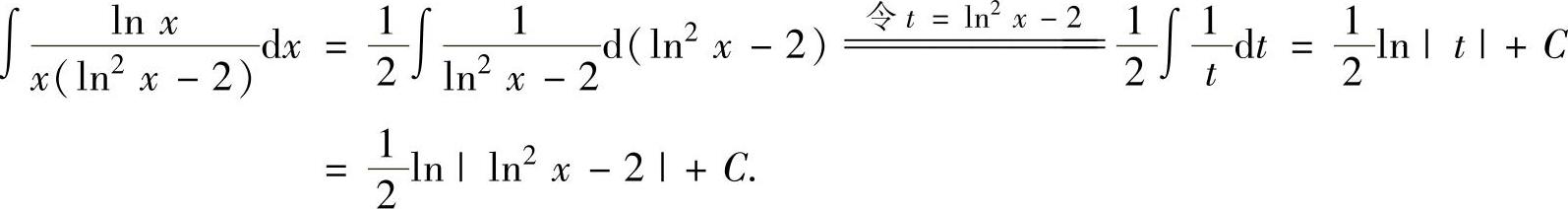
例2.1.2 求不定积分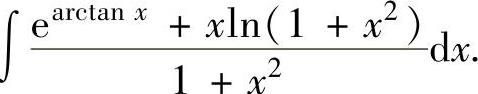
精解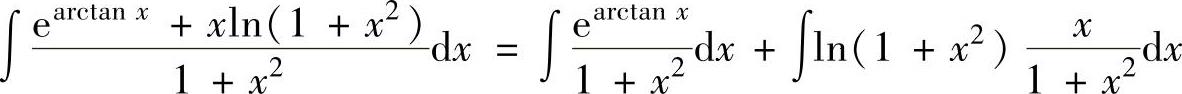 ,(1)
,(1)
其中,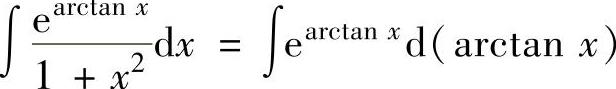
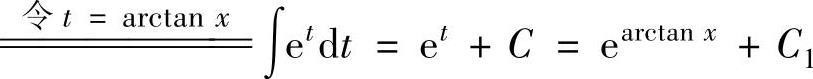 ,
,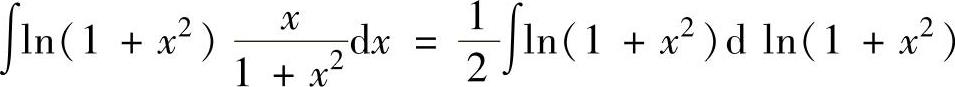

将它们代入式(1)得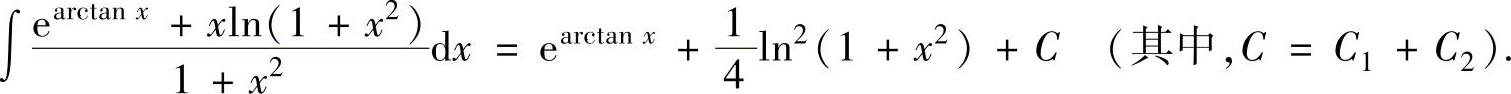
例2.1.3 求不定积分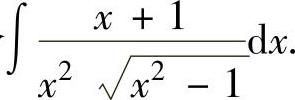
精解 由于被积函数中含有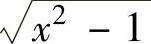 ,所以令x=sect.
,所以令x=sect.
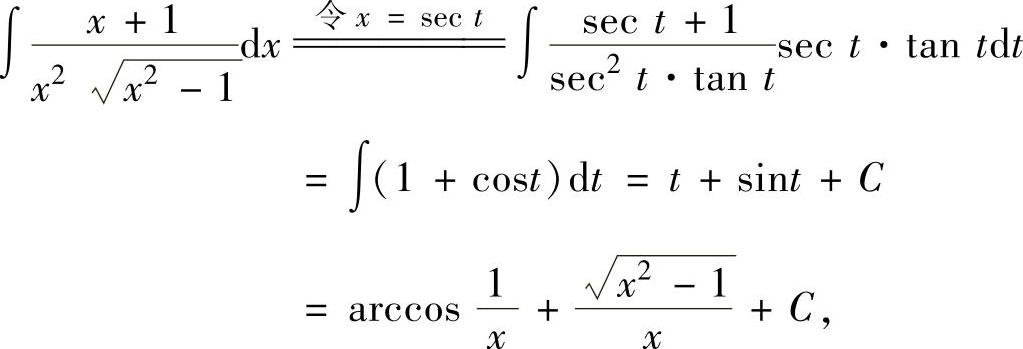
其中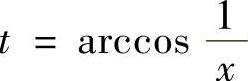 ,
,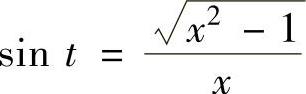 可从图2.1.3得到.
可从图2.1.3得到.
注 由于本题被积函数分母比较复杂,所以也考虑令母中的x这个因子去掉,具体如下: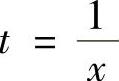 ,将其变得简单些,例如将分
,将其变得简单些,例如将分

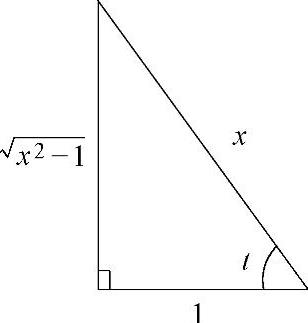
图 2.1.3
例2.1.4 求不定积分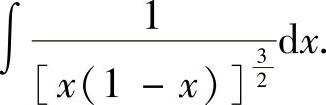
精解 由于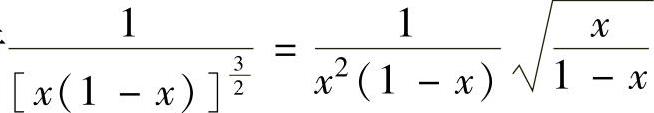 ,即被积函数中含根式
,即被积函数中含根式 ,所以令
,所以令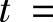
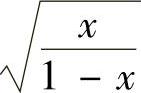 ,即
,即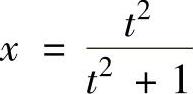 ,于是有
,于是有
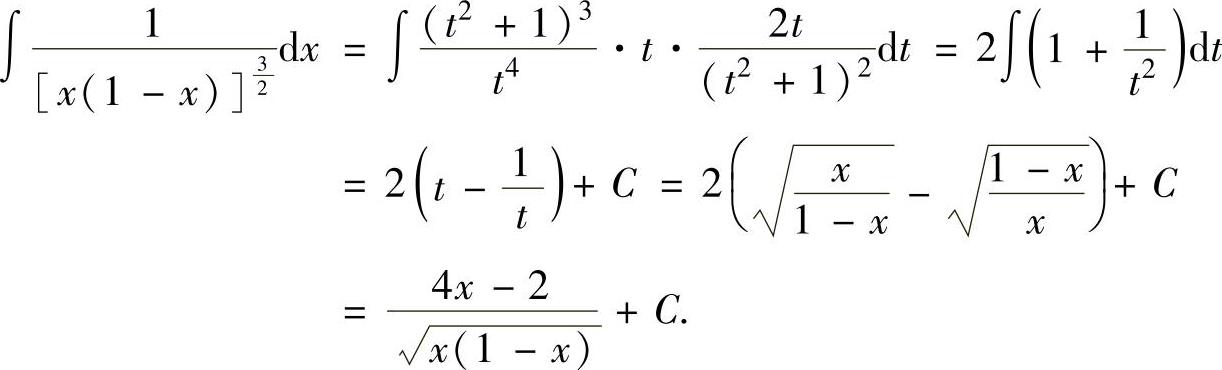
注 本题也可以用如下的变量代换求解:

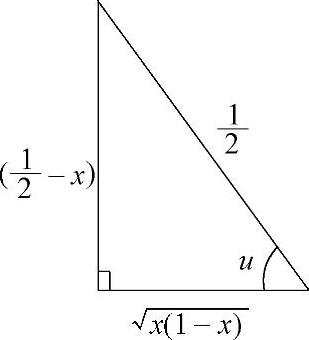
图 2.1.4
例2.1.5 求不定积分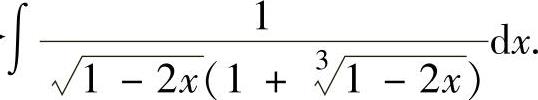
精解 由于被积函数中含有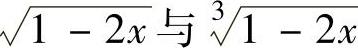 ,所以令
,所以令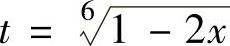 ,即
,即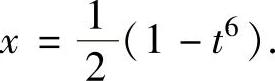
于是有
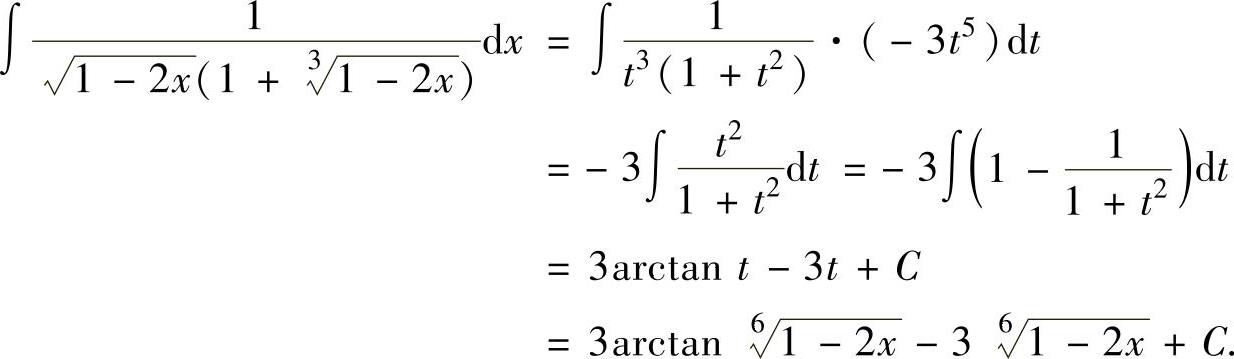
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

知识要点一、原函数与不定积分概念1.概念:原函数是积分学中的一个重要概念,求不定积分就是求被积函数的全体原函数,要在理解原函数概念的基础上,弄清不定积分与微分之间的内在关系,能根据积分与微分的互逆关系求不定积分.2.不定积分的性质:3.不定积分的法则与公式:公式要熟练掌握.二、直接积分法直接利用不定积分的公式和性质求函数不定积分.三、第一类换元积分法(凑微分法)设f(u)有原函数F(u),u=φ(......
2023-10-26

有些不定积分难以用凑微分的方法来积分,比如等.但此时若作适当的x=φ(t)变 换 后会变得容易积分,这种换元积分的方法称为第二类换元积分法,具体叙述如下.定理2设x=φ(t)有连续的导函数,且φ′(t)≠0,又设F(t)+C,则有其中φ-1(x)是x=φ(t)的反函数.证只需证明两个不定积分有相同的原函数即可.因为F(t)是f(φ(t))φ′(t)的原函数,记Φ(x)=F(φ-1(x)),则即......
2023-11-19

【主要内容】1.有理函数不定积分的计算方法设P(x),Q(x)分别是m,n(m,n都是自然数)次多项式,且它们是不可约的,则称∫PQ((xx))dx为有理函数的不定积分.当m≥n时,,其中,R(x)是m-n次多项式,P1(x)是r(r
2023-10-27

用牛顿—莱布尼茨公式计算定积分时,需要求出被积函数的原函数,由于用换元积分法和分部积分法可以求出一些函数的原函数,因此,在一定条件下,可以用换元积分法和分部积分法来计算定积分.下面讨论定积分的这两种计算方法.一、定积分的换元积分法定理5.6 若函数f(x)在区间[a,b]上连续,函数x=φ(t)在区间[α,β]上具有连续的导数,当t在区间[α,β]上变化时,x=φ(t)的值在[a,b]上变化,且φ......
2023-11-22

【主要内容】不定积分的分部积分法就是利用公式(其中,u(x),v(x)都具有连续的导数),将不定积分如果∫v(x)du(x)比较容易计算,则由上述公式就可算得注 用分部积分法计算不定积分∫时,应将它表示成∫的形式,即关于如何选择u(x),应遵循以下两个原则:(ⅰ)容易确定v(x),它是f(x)中除去u(x)后的剩余部分的一个原函数;较容易计算.具体地,如果f(x)是对数函数或反三角函数时,则取u(......
2023-10-27

一、第一类换元法在上一节中,虽已介绍了一些求原函数的方法,但这些方法在有些情况下是不够的.例如,∫cos2xdx就不易求解.如果令2x=u,可得代回原变量,得.一般地,设f(u)是u的连续函数,且∫f(u)du=F(u)+C,若u=φ(x)有连续的导数φ′(x),则∫f(φ(x))φ′(x)dx=F(φ(x))+C要证明上式成立,只需证明[F(φ(x))]′=f(φ(x))φ′(x)即可.因为[F......
2023-11-22

一、不定积分的概念原函数定义:设f(x)是定义某区间I上的已知函数,若存在一个函数F(x),对于该区间上每一点都满足:F′(x)=f(x)或dF(x)=f(x)dx,则称F(x)是f(x)在该区间I上的一个原函数.如已知f(x)=2x,由于F(x)=x2满足F′(x)=(x2)′=2x,所以F(x)=x2是f(x)=2x的一个原函数.同理,x2+1,x2-1,x2+10等也都是f(x)=2x的原函......
2023-11-20

一、原函数与不定积分定义4.1 设f(x)是定义在区间I上的函数,如果存在函数F(x),对于任意x∈I,都有F′(x)=f(x)或dF(x)=f(x)dx则称函数F(x)为函数f(x)在区间I上的一个原函数.例如,因为(sinx)′=cosx,则sinx是cosx的原函数.又因为(sinx+1)′=cosx,所以sinx+1也是cosx的原函数.由此例可以看出,一个函数若有原函数,则原函数可以不止......
2023-11-22
相关推荐