首页理论教育曲线渐近线的计算方法

曲线渐近线的计算方法

2023-10-27 理论教育版权反馈

【摘要】：【主要内容】曲线y=f（x）的渐近线有两类：1.铅直渐近线.如果x→x0（x→x0+，或x→x0-）时，f（x）→∞，则x=x0是曲线y=f（x）的一条铅直渐近线.2.非铅直渐近线.如果x→∞（x→+∞或x→-∞）时，，f（x）-ax→b，则y=ax+b是曲线y=f（x）的一条非铅直渐近线.当a≠0时，称非铅直渐近线y=ax+b为斜渐近线；当a=0时，称非铅直渐近线y=b为水平渐近线.【典型例题】

【主要内容】

曲线y=f（x）的渐近线有两类：

1.铅直渐近线.如果x→x0（x→x0+，或x→x0-）时，f（x）→∞，则x=x0是曲线y=f（x）的一条铅直渐近线.

2.非铅直渐近线.如果x→∞（x→+∞或x→-∞）时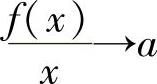，，f（x）-ax→b，则y=ax+b是曲线y=f（x）的一条非铅直渐近线.

当a≠0时，称非铅直渐近线y=ax+b为斜渐近线；当a=0时，称非铅直渐近线y=b为水平渐近线.

【典型例题】

例1.23.1 求曲线的渐近线方程.

精解先求所给曲线的铅直渐近线，再计算它的非铅直渐近线.

由于仅当x→0^+时，y→∞，所以，曲线y=（2x-1）ex¹仅有铅直渐近线x=0.由于，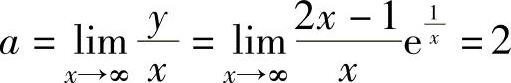

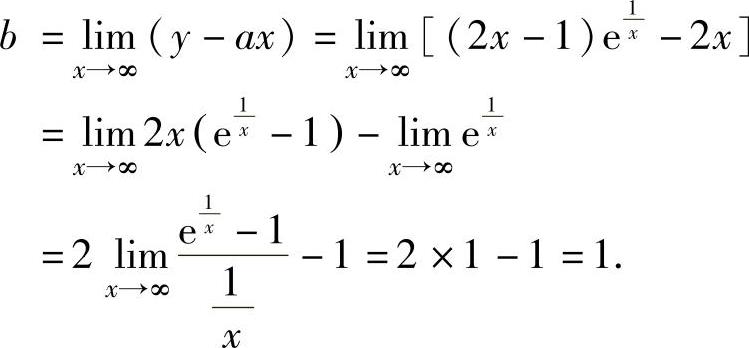
所以，曲线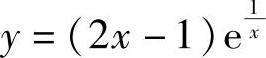仅有非铅直渐近线y=2x+1（斜渐近线）.

例1.23.2 （单项选择题）曲线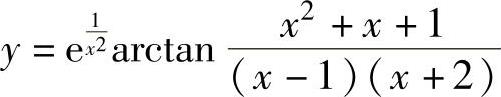的渐近线条数为（）.

A.1 B.2 C.3 D.4

精解先求所给曲线的铅直渐近线，再计算它的非铅直渐近线，由此得到所给曲线的渐近线条数.

由于仅当x→0时，y→∞，所以所给曲线仅有铅直渐近线x=0.(www.chuimin.cn)

由于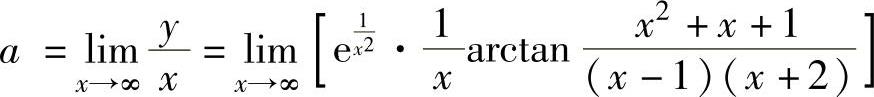

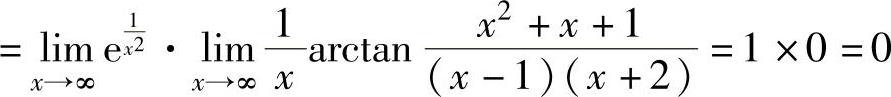
（其中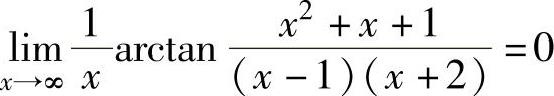，是因为x→∞时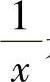，是无穷小，而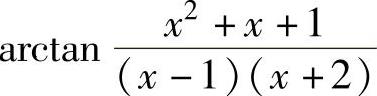

是有界函数），

所以所给曲线仅有非铅直渐近线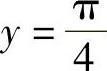（水平渐近线）.

因此本题选B.

例1.23.3 求曲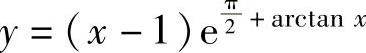线的渐近线.

精解显然所给曲线无铅直渐近线（这是因为没有无穷间断点）.由

于lim x不存在，因此分x→+∞和x→-∞情形分别计算非铅直渐近线.

由于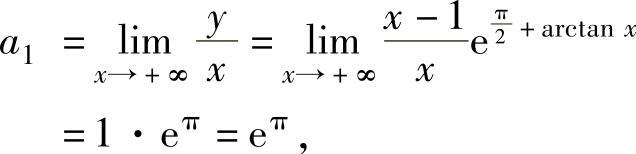

所以，所给曲线有非铅直渐近线y=eπx-2eπ.

由于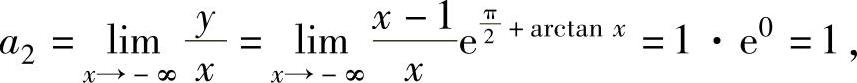

所以，所给曲线还有非铅直渐近线y=x-2.