首页理论教育曲线凹凸性、拐点计算：全面复习与解析

曲线凹凸性、拐点计算：全面复习与解析

2023-10-27 理论教育版权反馈

【摘要】：1.曲线凹凸性及其判定方法在某个区间内，如果曲线位于其上任意一点的切线的上方（下方），则称曲线在该区间内为凹的（凸的）.曲线y=f（x）在区间I上凹凸性的判定方法是：设函数f（x）在I上二阶可导.如果f″（x）>0（x∈I），则曲线y=f（x）在I上是凹的；如果f″（x）<0（x∈I），则曲线y=f（x）在I上是凸的.2.曲线拐点及其计算方法设函数f（x）连续，则曲线y=f（x）上的凹弧与凸弧的分

1.曲线凹凸性及其判定方法

在某个区间内，如果曲线位于其上任意一点的切线的上方（下方），则称曲线在该区间内为凹的（凸的）.

曲线y=f（x）在区间I上凹凸性的判定方法是：

设函数f（x）在I上二阶可导.如果f″（x）>0（x∈I），则曲线y=f（x）在I上是凹的；如果f″（x）<0（x∈I），则曲线y=f（x）在I上是凸的.

2.曲线拐点及其计算方法

设函数f（x）连续，则曲线y=f（x）上的凹弧与凸弧的分界点称为该曲线的拐点.

曲线y=f（x）（f（x）是连续函数）的拐点可按以下步骤计算：

（1）在f（x）的定义域上，求方程f″（x）=0的实根和使f″（x）不存在的点，设为x₁，x₂，…，xn；

（2）对由步骤（1）算得的每个x_i，如果在其两侧邻近f″（x）为异号，则（x_i，f（x_i））是曲线y=f（x）的一个拐点，否则点（x_i，f（x_i））不是曲线y=f（x）的拐点.

【典型例题】

例1.22.1 计算下列曲线y=f（x）的凹凸区间（即曲线y=f（x）凹弧的区间与凸弧的区间）与拐点：

（1）；

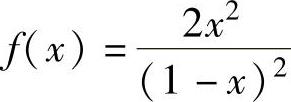（2）

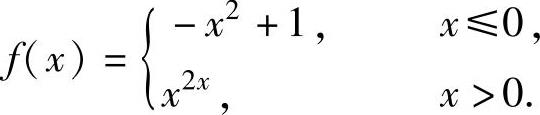
精解（1）y=f（x）的定义域为（-∞，1）∪（1，+∞），且在其上二阶可导，

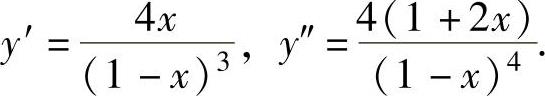
显然使y″=0的点为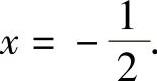据此列表如下：

由表可知，曲线y=f（x）的凸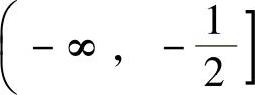区间为，凹区间为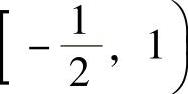和（1，+∞），拐点

为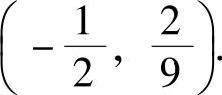(www.chuimin.cn)

（2）y=f（x）的定义域为（-∞，+∞），且在其上连续，此外有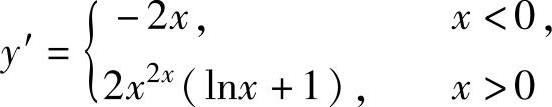（这里不必确定y在点x=0处的可导性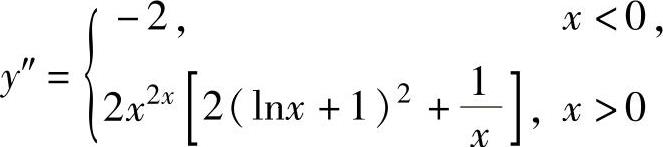），（这里不必确定y′在点x=0处的可导性），

由此可知，曲线y=f（x）（连续函数）的凸区间为（-∞，0]，凹区间为[0，+∞），拐点为（0，1）.

例1.22.2 （单项选择题）曲线y=（x-1）（x-2）2（x-3）3（x-4）4的拐点是（）.

A.（1，0） B.（2，0） C.（3，0） D.（4，0）

精解由

可得y=（x-1）（x-2）2（x-3）3（x-4）4的概图如图1.22.2所示.由图可知点（3，0）是所给曲线的拐点.

因此本题选C.

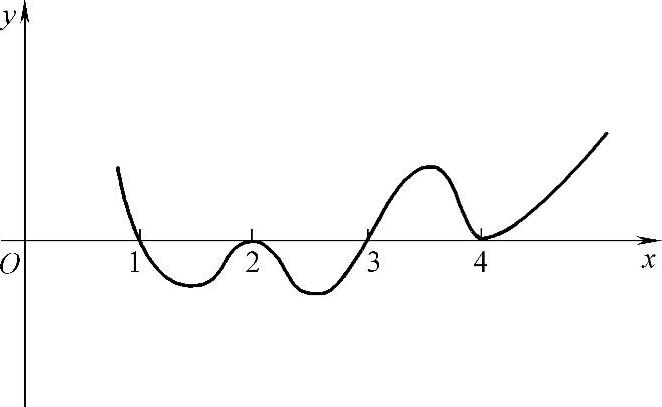
图 1.22.2

例1.22.3 （单项选择题）设函数f（x）满足f（x）=-f（-x），x∈（-∞，+∞），且在（0，+∞）上f′（x）>0，f″（x）>0，则f（x）在（-∞，0）上（）.

A.单调增加且其图形是凹的

B.单调增加且其图形是凸的

C.单调减少且其图形是凹的

D.单调减少且其图形是凸的

精解由f（x）是奇函数知f′（x）是偶函数，f″（x）是奇函数，所以在（-∞，0）上f′（x）>0，f″（x）<0，即在（-∞，0）上f（x）单调增加且其图形是凸的.

因此本题选B.