首页理论教育不等式导数的证明-基础篇全面复习与常考知识点解析

不等式导数的证明-基础篇全面复习与常考知识点解析

2023-10-27 理论教育版权反馈

【摘要】：【主要内容】函数不等式f（x）0（x∈（a，b））及时，有F（

【主要内容】

函数不等式f（x）<g（x）（x∈（a，b））的证明，总是先作辅助函数.通常作辅助函数F（x）=g（x）-f（x）.如果这样的F（x）不易求导，或求导后的表达式比较复杂，其符号不易确定，则可先对不等式作适当的等价变形，例如将三角函数集中到不等号的一边；将反三角函数和对数函数分散到不等号两边等，再作辅助函数.

如果F（x）在（a，b）内可导，则当F′（x）>0（x∈（a，b））及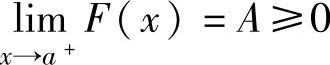时，有

F（x）>A≥0，即f（x）<g（x）（x∈（a，b））；当F′（x）<0（x∈（a，b））及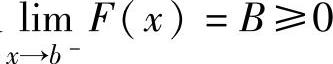

时，有F（x）>B≥0，即f（x）<g（x）（x∈（a，b））；当存在x₀∈（a，b），使得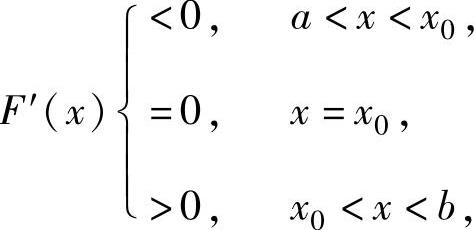且F（x₀）=c>0时有

F（x）≥c>0，即f（x）>g（x）（x∈（a，b））.

【典型例题】

例1.20.1 证明：当x∈（0，1）时，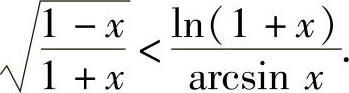

精解需将ln（1+x）与arcsinx分散到不等号的两边，故将欲证的不等式改写为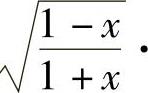

arcsinx<ln（1+x），或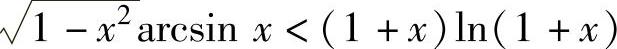.于是作辅助函数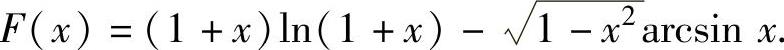

显然，它在（0，1）内可导且，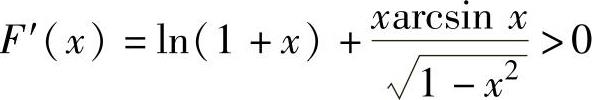

所以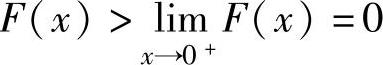.从而当x∈（0，1）时有

例1.20.2 证明：当x∈（0，1）时，（1+x）ln²（1+x）<x².

精解如作辅助函数F₁（x）=x²-（1+x）ln²（1+x），则F₁′（x）的表达式比较复杂，不易判别其符号，因此先将待证不等式改写为

于是作辅助函数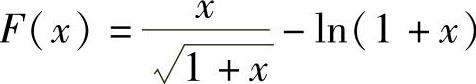，则F（x）在（0，1）内可导且

由此可知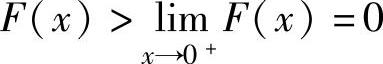，，从而当x∈（0，1）时有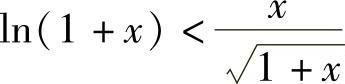，即（1+x）ln²（1+x）<x².

例1.20.3 设x∈（0，2），证明：4xlnx≥x²+2x-3.(www.chuimin.cn)

精解将欲证不等式改写成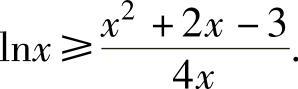记F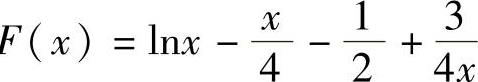，则F（x）在

（0，2）内可导，且

所以，对x∈（0，2）有F（x）≥F（1），即4xlnx≥x²+2x-3.

例1.20.4 设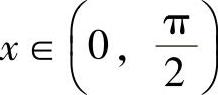，证明：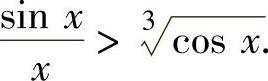

精解将三角函数集中到不等号的左边，欲证的不等式改写成

因此作辅助函数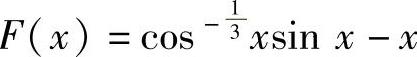，则它在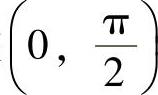内二阶可导且

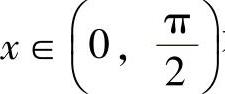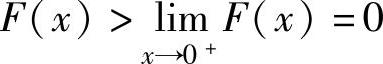所以，F（x）在内单调增加，由此得到，对有，即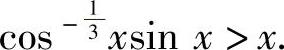

于是对x∈（0，1）有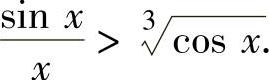

例1.20.5 设e<a<b<e²，证明：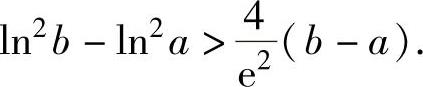

精解将欲证不等式中的b改为x（将a改为x也可以），转化为函数不等式

为了证明这个函数不等式，作辅助函数

则它在（a，e²）内二阶可导且，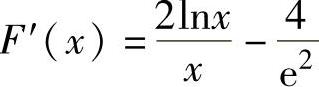

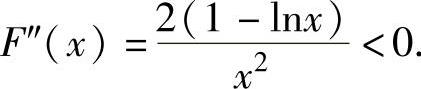
所以，F′（x）在（a，e²）内单调减少，从而对x∈（a，e²）有

即F（x）在（a，e²）内单调增加，所以对于b∈（a，e²）有

F（b）>F（a）=0.从而证得，对e<a<b<e²有