【主要内容】1.二元函数极值的定义设二元函数f(x,y)在点(x0,y0)的某个邻域内有定义.如果在此邻域内对任意(x,y)≠(x0,y0)都有f(x,y)
2023-10-27
【主要内容】
1.函数极值的定义
设函数f(x)在点x0的某个充分小的邻域内有定义.如果对这个邻域内每个不为x0的x都有f(x)>f(x0)(f(x)<f(x0)),则称f(x0)是f(x)的一个极小值(极大值),称x0为f(x)的一个极小值点(极大值点).极小值与极大值统称极值,极小值点与极大值点统称极值点.
2.函数极值的必要条件
设x0是函数f(x)的极值点,则f′(x0)=0或f′(x0)不存在.
由此可知,f(x)的可能极值点来自两个方面:f′(x)为0的点(称为f(x)的驻点)和f′(x)不存在的点.
3.函数极值的充分条件
第一充分条件:设函数f(x)在点x0处连续,在点x0的某个去心邻域(x0-δ,x0)∪(x0,x0+δ)(δ>0)内可导.
(1)如果x∈(x0-δ,x0)时f′(x)>0,x∈(x0,x0+δ)时f′(x)<0,则f(x0)是f(x)的一个极大值;
(2)如果x∈(x0-δ,x0)时f′(x)<0,x∈(x0,x0+δ)时f′(x)>0,则f(x0)是f(x)的一个极小值;
(3)如果x∈(x0-δ,x0)∪(x0,x0+δ)时f′(x)的符号保持不变,则f(x0)不是f(x)的极值.
第二充分条件:设函数f(x)在点x0处二阶可导,且f′(x0)=0,f″(x0)≠0,则
(1)当f″(x0)<0时,f(x0)是f(x)的一个极大值;
(2)当f″(x0)>0时,f(x0)是f(x)的一个极小值.
4.函数极值的计算步骤
函数极值可按以下步骤计算:
(1)计算f(x)的定义域;
(2)在定义域内计算f(x)的所有可能极值点(即f(x)的驻点与导数f′(x)不存在的点,此外将分段函数的分段点也列入可能极值点),记为x1,x2,…,xn.
(3)由第一充分条件或第二充分条件逐一判定x1,x2,…,xn是否为f(x)的极大值点或极小值点.如果是,算出对应的函数值,即得f(x)的极值.
【典型例题】
例1.18.1 (单项选择题)设函数f(x)在点x=0的某个邻域内连续,且满足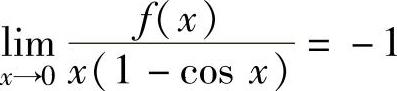 ,则x=0是().
,则x=0是().
A.f(x)的驻点,且为极大值点 B.f(x)的驻点,且为极小值点
C.f(x)的驻点,但不是极值点 D.不是f(x)的驻点
精解 由 ,从而f′(0)=0,即x=0
,从而f′(0)=0,即x=0
是f(x)的驻点,且f(0)=0.
另由题设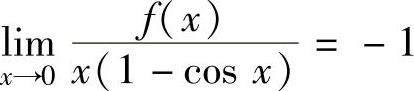 知在(-δ,0)∪(0,δ)(δ是某个充分小的正数)内
知在(-δ,0)∪(0,δ)(δ是某个充分小的正数)内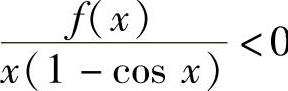 ,所以,当x∈(-δ,0)时,f(x)>0=f(0);当x∈(0,δ)时,f(x)<0=
,所以,当x∈(-δ,0)时,f(x)>0=f(0);当x∈(0,δ)时,f(x)<0=
f(0).由此可知,x=0不是f(x)的极值点.
因此本题选C.
例1.18.2 (单项选择题)设偶函数f(x)在点x=0处二阶可导,且f″(0)≠0,则x=0( ).(www.chuimin.cn)
A.是f(x)的驻点,但不是极值点
B.不是f(x)的驻点,但是极值点
C.是f(x)的驻点和极值点
D.既不是f(x)的驻点,又不是极值点
精解 由f(x)是偶函数知,f′(x)是奇函数,并且在点x=0处连续,所以f′(0)=0,即x=0是f(x)的驻点.
由于f″(0)≠0,所以x=0是f(x)的极值点.
因此本题选C.
注 当f(x)是可导的偶函数(奇函数)时,f′(x)是奇函数(偶函数).
例1.18.3 求函数f(x)=|x|e-|x-1|的极值.
精解 f(x)的定义域为(-∞,+∞),且
所以f(x)的可能极值点为x=-1(驻点),x=0,1(都是分段点),据此列表如下:
由表可知,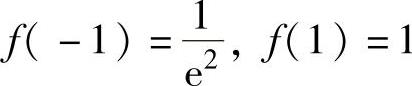 都是f(x)的极大值,f(0)=0是f(x)的极小值.
都是f(x)的极大值,f(0)=0是f(x)的极小值.
例1.18.4 设函数y=y(x)由方程2y3-2y2+2xy-x2=1确定,求y=y(x)的驻点,并判别它是否为极值点?
精解 所给方程两边对x求导得
3y2y′-2yy′+y+xy′-x=0.(1)
设驻点为x0,记y0=y(x0),将它们以及y′(x0)=0代入式(1)得y0=x0,将x=x0,y=y0=x0代入题设的方程得2x30-x20=1,即2x30-x20-1=0.由于(2x30-2x02)+(x20-1)=(x0-1)(2x20+x0+1),所以,方程2x03-x20-1=0有且仅有实根x0=1,即y=y(x)只有唯一的驻点x=1.
式(1)的两边对x求导得
6y(y′)2+3y2y″-2(y′)2-2yy″+2y′+xy″-1=0,(2)
将x=1,y=1以及y′=0代入式(2)得
所以x=1是y=y(x)的极小值点.
例1.18.5 求在点x=1处有极大值6,在点x=3处有极小值2的最低次多项式(它的最高次系数为1)的表达式.
精解 对一次多项式、二次多项式等逐一检验,求得满足要求的多项式.
由于一次多项式无极大值与极小极,所以不满足要求.
由于二次多项式(它的图形是抛物线)不会既有极大值又有极小值,所以也不满足要求.
下面考虑三次多项式x3+ax2+bx+c.
记y=x3+ax2+bx+c,则y′=3x2+2ax+b,y″=6x+2a.于是由题设知,a,b,c应满足以下方程和不等式组: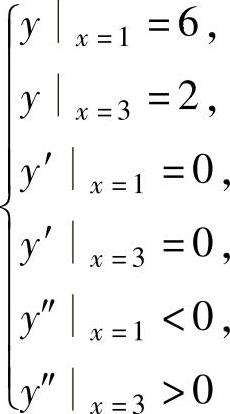 即
即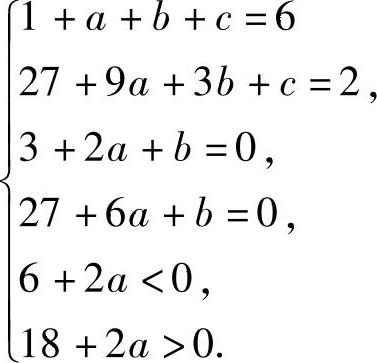
解此方程和不等式组得a=-6,b=9,c=2,所以符合题意的多项式为x3-6x2+9x+2.
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

【主要内容】1.二元函数极值的定义设二元函数f(x,y)在点(x0,y0)的某个邻域内有定义.如果在此邻域内对任意(x,y)≠(x0,y0)都有f(x,y)
2023-10-27

【主要内容】计算函数的导数的基础是求导基本公式和四则运算法则.求导基本公式:(1)C′=0(C是常数),(2)(xμ)′=μxμ-1,(3)(ax)′=axlna(常数a>0但a≠1),特别地,(ex)′=ex,(4),特别地,,(5)(sinx)′=cosx, (6)(cosx)′=-sinx,(7)(tanx)′=sec2x, (8)(cotx)′=-csc2x,(9)(secx)′=secx......
2023-10-27

微分方程虽然也不是很好解,但是相对于解泛函已经要容易许多了。参考阅读//No. 9 映射,第22页No. 50 导数,第104页No. 55 微分方程,第114页No. 66 极小曲面,第136页右图:当一个函数达到最大值或者最小值时,它的导数为零。通常来讲,要解决一个泛函问题,我们就把它转化为一个有希望解决的微分方程问题。......
2023-11-22

定义 设函数z=f(x,y)在点(x0,y0)的某个邻域内有定义,对于该邻域内异于点(x0,y0)的点(x,y):(1)若f(x,y)<f(x0,y0),则称函数在点(x0,y0)有极大值f(x0,y0);(2)若f(x,y)>f(x0,y0),则称函数在点(x0,y0)有极小值f(x0,y0).极大值、极小值统称为极值.使函数取得极值的点称为极值点.例1 函数z=3x2+4y2在点(0,0)处有......
2023-10-19

解:要使材料最省,就是要罐头筒的总表面积最小.设罐头的底半径为r,高为h,如图3.5所示,则它的侧面积为2πrh,底面积为πr2,因此总表面积为图3.5于是得出结论:当所做罐头筒的高和底直径相等时,所用材料最省.习题3.21.求函数的单调区间和极值.f=x2-2x+4;f=x2-6x;y=2x3-3x2;y=x-ln(1+x);f=x3-12x.2.运用极值的第二定理求极值.f=x2-2x;f=x4-2x2.3.求函数的最值.f=x2-2x+1,x∈[-1,2];f=x2-2x,x∈[0,2];f=x3-3x,x∈[0,2];f=x4-2x2,x∈[0,2].4.已知x+y=s,运用极值第二定理证明......
2023-11-20

定义1凡是满足方程f′(x)=0的点x称为函数f(x)的驻点.根据导数的几何意义,在曲线y=f(x)上驻点处的切线是水平的.图3-9在图3-9中,考察函数f(x)在[a,b]上的极值与最值,发现:函数f(x)在点x1,x2,x3处取得极大值,函数f(x)在x′1,x′2,x′3处取得极小值;其最大值为f(b),最小值为f(x′2).观察该图还发现:函数在一个区间内可以有若干个极大值与极小值,函数......
2023-11-19

5.曲线L:xy=1(x>0)上求一点,使函数f(x,y)=x2+2y2达到最小值.复习题八一、填空题二、选择题4.设z=xy,则dz=().A.dx+dyB.-dx-dyC.xdx+ydyD.yd......
2023-11-20
相关推荐