首页理论教育拉格朗日中值定理和柯西中值定理的应用

拉格朗日中值定理和柯西中值定理的应用

2025-09-30 理论教育版权反馈

【摘要】：【主要内容】1.拉格朗日中值定理设函数f（x）在闭区间[a，b]上连续，在开区间（a，b）内可导，则存在ξ∈（a，b），使得f（b）-f（a）=f′（ξ）（b-a）.2.柯西中值定理设函数f（x）和g（x）都在闭区间[a，b]上连续，在开区间（a，b）内可导，且g′（x）≠0（x∈（a，b）），则存在ξ∈（a，b），使得当函数f（x）在[a，b]上连续，在（a，b）内可导，但不易确定f（a）=f（

【主要内容】

1.拉格朗日中值定理

设函数f（x）在闭区间[a，b]上连续，在开区间（a，b）内可导，则存在ξ∈（a，b），使得

f（b）-f（a）=f′（ξ）（b-a）.

2.柯西中值定理

设函数f（x）和g（x）都在闭区间[a，b]上连续，在开区间（a，b）内可导，且g′（x）≠0（x∈（a，b）），则存在ξ∈（a，b），使得

当函数f（x）在[a，b]上连续，在（a，b）内可导，但不易确定f（a）=f（b），或f（a）=f（b）根本不成立时要证明存在ξ∈（a，b），使得某个关于f′（ξ）的表达式成立，显然不适合

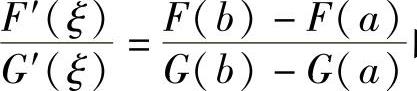应用罗尔定理.但是，如果上述的某个关于f′（ξ）的表达式可以表示成的形式（其中F（x）是辅助函数），或者可以表示成的形式

（其中F（x）和G（x）都是辅助函数），则可分别考虑应用拉格朗日中值定理与柯西中值定理.

【典型例题】

例1.14.1 设函数f（x）在[a，b]上连续，在（a，b）内可导.证明：存在ξ∈（a，b），使得

精解由f（ξ）+ξf′（ξ）=[xf（x）]′_x=ξ知，可取F（x）=xf（x）为辅助函数.显然F（x）在[a，b]上连续，在（a，b）内可导，所以由拉格朗日中值定理知，存在ξ∈（a，b），使得，即

例1.14.2 设函数f（x）在[0，1]上连续，在（0，1）内可导，且f（0）=0，f（1）=1.证明：

（1）存在ξ∈（0，1），使得f（ξ）=1-ξ；

（2）存在两个不同点η₁，η₂∈（0，1），使得f′（η₁）f′（η₂）=1.

精解（1）由于本小题的欲证等式中不出现f的导数，所以可考虑应用连续函数零点定理，具体如下：

将欲证等式中的ξ改为x得f（x）=1-x.于是作辅助函数(https://www.chuimin.cn)

F（x）=f（x）+x-1.显然，它在[0，1]上连续，且F（0）F（1）=（-1）×1<0，所以由连续函数零点定理知，存在ξ∈（0，1），使得F（ξ）=0，即f（ξ）=1-_ξ.

（2）ξ将[0，1]划分成两个小区间[0，ξ]和[ξ，1].显然，f（x）在这两个小区间上都满足拉格朗日中值定理的条件，所以由该定理知存在_η1∈（0，ξ）和η₂∈（ξ，1），使得，，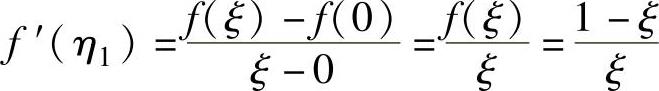

即存在两个不同点_η1，η₂∈（0，1），使得

例1.14.3 设函数f（x）在[a，b]上连续，在（a，b）内二阶可导，且f（a）=f（b）=0，f+′（a）>0.证明：存在ξ∈（a，b），使得f″（ξ）<0.

精解由于要证明的是存在ξ∈（a，b），使得f″（ξ）<0，而不是f″（ξ）=0，所以不宜使用罗尔定理，因此考虑应用拉格朗日中值定理.

由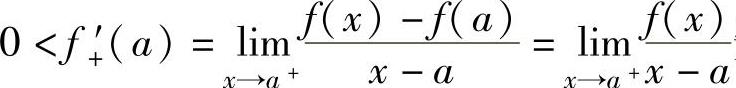知，存在x₀∈（a，b），使得f（x₀）>0.

显然，f（x）在[a，x₀]和[x₀，b]上都满足拉格朗日中值定理条件，所以，存在ξ₁∈（a，x₀）和ξ₂∈（x₀，b），使得，

由于f′（x）在[ξ₁，ξ₂]上满足拉格朗日中值定理条件，因此存在ξ∈（ξ₁，ξ₂）⊂（a，b），使得

例1.14.4 设函数f（x）在[a，b]上连续，在（a，b）内可导且f′（x）≠0.证明：存在ξ，η∈（a，b），使得

精解由于欲证的等式可以改写为

于是，由拉格朗日中值定理知，只要证明存在η∈（a，b），使得

显然，只要对e^x和f（x）在[a，b]上使用柯西中值定理即可.具体证明如下：

由于e^x和f（x）在[a，b]上连续，在（a，b）内可导且f′（x）≠0，所以由柯西中值定理知，存在η∈（a，b），使得

由于f（x）在[a，b]上满足拉格朗日中值定理条件，所以存在ξ∈（a，b），使得

f（b）-f（a）=f′（ξ）（b-a）.（2）

将式（2）代入式（1）知，存在ξ，η∈（a，b），使得