罗尔定理和应用-基础篇全面复习与常考知识点解析

2023-10-27 理论教育版权反馈

【摘要】：【主要内容】1.罗尔定理设函数f（x）在[a，b]上连续，在（a，b）内可导，且f（a）=f（b），则存在ξ∈（a，b），使得f′（ξ）=0.罗尔定理有各种推广形式，例如（1）设函数f（x）在（a，b）内可导，且与存在且相等，则存在ξ∈（a，b），使得f′（ξ）=0.（2）设函数f（x）在[a，+∞）上连续，在（a，+∞）上可导，且，则存在ξ∈（a，+∞），使得f′（ξ）=0.2.罗尔定理应用方法

【主要内容】

1.罗尔定理

设函数f（x）在[a，b]上连续，在（a，b）内可导，且f（a）=f（b），则存在ξ∈（a，b），使得f′（ξ）=0.

罗尔定理有各种推广形式，例如

（1）设函数f（x）在（a，b）内可导，且与存在且相等，则存在ξ∈（a，

b），使得f′（ξ）=0.

（2）设函数f（x）在[a，+∞）上连续，在（a，+∞）上可导，且，则存在ξ∈（a，+∞），使得f′（ξ）=0.

2.罗尔定理应用方法

罗尔定理往往用于证明以下三类问题：

（1）当函数f（x）在[a，b]上连续，在（a，b）内可导，且满足某些其他条件时，证明存在ξ∈（a，b），使得f′（ξ）=0成立.

对于这类问题，只要根据题中所给的“某些其他条件”设法找到位于[a，b]上的使得f（x₁）=f（x₂）（x₁<x₂）的两点x₁，x₂即可.

（2）当函数f（x）在[a，b]上连续，在（a，b）内可导，且满足某些其他条件时，证明存在ξ∈（a，b），使得某个关于f′（ξ）的等式成立.

对这类问题需要先作辅助函数，其步骤如下：

将待证等式中的ξ改为x，并将等号右边的式子移至左边，将左边函数或左边函数与某个在（a，b）内恒为正（或恒为负）的因子之积表示成某个函数F（x）的导数F′（x），则取F（x）为辅助函数.

然后，检验辅助函数F（x）在[a，b]上连续，在（a，b）内可导，并设法找到位于[a，b]上的使得F（x₁）=F（x₂）（x₁<x₂）的两点x₁，x₂即可.

（3）当函数f（x）在[a，b]上连续，在（a，b）内二阶可导，且满足某些其他条件时，证明存在ξ∈（a，b）使得f″（ξ）=0.

对这类问题，只要根据题中所给的“某些其他条件”，想法找到位于[a，b]上的使得f（x₁）=f（x₂）=f（x₃）（x₁<x₂<x₃）的三点x₁，x₂，x₃即可.这是因为由罗尔定理知存在ξ₁∈（x₁，x2）和ξ₂∈（x₂，x₃），使得f′（ξ₁）=f′（ξ₂）.再对f′（x）在[ξ₁，ξ₂]上应用罗尔定理得存在ξ∈（ξ₁，ξ₂）⊂（a，b），使得f″（ξ）=0.

【典型例题】

例1.13.1 设函数f（x）在[a，b]上连续，在（a，b）内可导，且f（a）=f（b）=1.证明：存在ξ∈（a，b），使得f′（ξ）+f（ξ）=1.

精解先作辅助函数，将欲证等式中的ξ改为x得

f′（x）+f（x）=1，即[f（x）-1]′+[f（x）-1]=0.上式两边同乘e^x得

e^x[f（x）-1]′+e^x[f（x）-1]=0，即{e^x[f（x）-1]}′=0.因此，记F（x）=e^x[f（x）-1]（辅助函数），显然它在[a，b]上连续，在（a，b）内可导，且F（a）=F（b）=0，所以由罗尔定理知，存在ξ∈（a，b），使得F′（ξ）=0，即

f′（ξ）+f（ξ）=1.

例1.13.2 设函数f（x），g（x）都在[0，1]上连续，在（0，1）内可导，且f（0）=g（1）

=0.证明：

（1）存在ξ∈（0，1），使得f′（ξ）g（ξ）+f（ξ）g′（ξ）=0；

（2）存在η∈（0，1），使得ηf′（η）+kf（η）=f′（η）（k为正数）.

精解（1）将欲证等式中的ξ改为x得f′（x）g（x）+f（x）g′（x）=0，

即[f（x）g（x）]′=0.

因此记F₁（x）=f（x）g（x）（辅助函数），显然它在[0，1]上连续，在（0，1）内可导，且

F₁（0）=F₁（1）=0，所以由罗尔定理知，存在ξ∈（0，1），使得F₁′（ξ）=0，即f′（ξ）g（ξ）+f（ξ）g′（ξ）=0.(www.chuimin.cn)

（2）将待证等式中的η改为x得xf′（x）+kf（x）=f′（x），

即（x-1）f′（x）+kf（x）=0.

上式两边同乘以（x-1）k-1得（x-1）kf′（x）+k（x-1）k-1f（x）=0，

即[（x-1）kf（x）]′=0.

因此记F₂（x）=（x-1）kf（x）（辅助函数），显然它在[0，1]上连续，在（0，1）内可导，且

F₂（0）=F₂（1）=0，所以由罗尔定理知，存在η∈（0，1），使得F₂′（η）=0，即η^f′（η）+kf（η）=f′（η）.

例1.13.3 设函数f（x）在[0，3]上连续，在（0，3）内可导，且f（0）+f（1）+f（2）=3，

f（3）=1.证明：存在ξ∈（0，3），使得f′（ξ）=0.

精解由于本题是证明存在ξ∈（0，3），使得f′（ξ）=0，所以不必作辅助函数，只要

找到使f（x₁）=f（x₂）的两点x₁，x₂∈（0，3）（x₁<x₂）即可.

显然可取x₂=3，则f（x₂）=1.

由于f（x）在[0，2]上连续，所以f（x）在[0，2]上有最大值M和最小值m，于是对，

由连续函数的介值定理知，存在x₁∈[0，2]，使得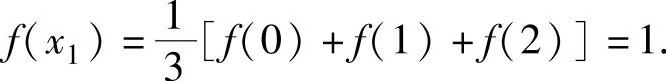

由于f（x）在[x₁，x₂]上连续，在（x₁，x₂）内可导，且f（x₁）=f（x₂）=1，所以由罗尔定理知，存在ξ∈（x₁，x₂）⊂（0，3），使得f′（ξ）=0.

例1.13.4 设函数f（x）在[a，b]上二阶可导，且f（a）=f（b）=0，f+′（a）·f-′（b）>0.证明：

（1）存在ξ∈（a，b），使得f（ξ）=0；

（2）存在η∈（a，b），使得f″（η）=0.

精解（1）由于本小题是证明存在ξ∈（a，b），使得f（ξ）=0，故可考虑应用零点定理，于是根据f+′（a）·f-′（b）>0，设法找到x1，x2∈（a，b）（x1<x2），使得f（x1）·f（x2）<0.

由于f+′（a）·f-′（b）>0，不妨设f+′（a）>0，f-′（b）>0.于是由导数定义得

由此可知，存在x₁，x₂∈（a，b）（x₁<x₂），使得f（x₁）>0，f（x₂）<0.于是由连续函数零点定理可得，存在ξ∈（x₁，x₂）⊂（a，b），使得f（ξ）=0.

（2）由于本小题是证明存在η∈（a，b），使得f″（η）=0，所以只要在[a，b]上找到不同的三点x₁，x₂，x₃使得f（x₁）=f（x₂）=f（x₃）即可.

由题设和（1）的证明知，[a，b]上有三个不同点a，ξ，b，它们满足

f（a）=f（ξ）=f（b）.

于是由f（x）在[a，b]上二阶可导知，存在η∈（ξ₁，ξ₂）⊂（a，b），使得f″（η）=0.

例1.13.5 设函数f（x），g（x）都在[a，b]上连续，在（a，b）内二阶可导且存在相等的最大值，以及f（a）=g（a），f（b）=g（b）.证明：存在ξ∈（a，b），使得f″（ξ）=g″（ξ）.

精解由于要证明存在ξ∈（a，b），使得f″（ξ）=g″（ξ），可作辅助函数F（x）=f（x）-g（x），使问题转换成证明存在ξ∈（a，b），使得F″（ξ）=0.为此只要找到[a，b]上的不同三点x₁，x₂，x3（x1<x₂<x₃），使得f（x₁）=f（x₂）=f（x₃）即可.具体证明如下：

记F（x）=f（x）-g（x），则由题设知F（x）在[a，b]上连续，在（a，b）内二阶可导，且F（a）=F（b）=0.显然，可取x₁=a，x₃=b.此外，设f（x），g（x）分别在（a，b）内的点c和点d处取到最大值M.不妨设c≤d.

当c<d时，F（c）=f（c）-g（c）=M-g（c）≥0，F（d）=f（d）-g（d）=f（d）-M≤0，则由连续函数的零点定理（推广形式）知存在x₂∈[c，d]，使得F（x₂）=0.

当c=d时，F（c）=f（c）-g（c）=M-M=0，此时可取x₂=c.

由上所述知，存在点a，c，b（a<c<b），使得F（a）=F（c）=F（b），所以存在ξ∈（a，b），使得F″（ξ）=0，即f″（ξ）=g″（ξ）.

罗尔定理和应用-基础篇全面复习与常考知识点解析

相关推荐