定理1 如果函数u=φ(t)及v=ψ(t)都在点t可导,函数z=f(u,v)在对应点(u,v)处具有连续偏导数,则复合函数z=f[φ(t),ψ(t)]在点t处可导,且其导数可用下列公式计算定理1可推广到复合函数的中间变量多于两个的情形.例如,设z=f(u,v,ω),u=φ(t),v=ψ(t),w=ω(t)复合而得复合函数则在与定理相类似的条件下,复合函数在点t可导,且其导数可用下列公式计算式(8.......
2025-09-30
【主要内容】
计算函数的导数的基础是求导基本公式和四则运算法则.
求导基本公式:
(1)C′=0(C是常数),(2)(xμ)′=μxμ-1,
(3)(ax)′=axlna(常数a>0但a≠1),特别地,(ex)′=ex,
(4)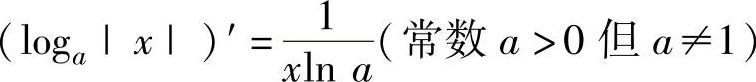 ,特别地,
,特别地,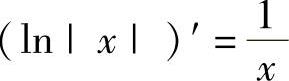 ,
,
(5)(sinx)′=cosx, (6)(cosx)′=-sinx,
(7)(tanx)′=sec2x, (8)(cotx)′=-csc2x,
(9)(secx)′=secxtanx, (10)(cscx)′=-cscxcotx,
(11)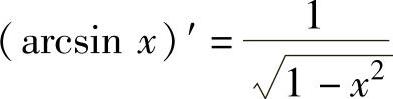 ,(12)
,(12)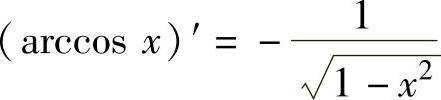 ,
,
(13)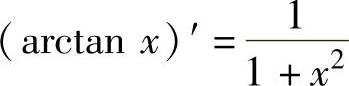 ,(14)
,(14)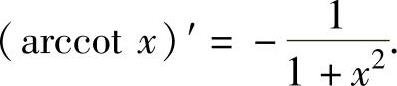
导数的四则运算法则:
设u(x),v(x)可导,则u(x)±v(x),u(x)v(x)以及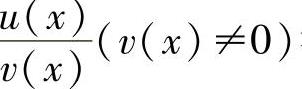 都可导,且
都可导,且
除此以外,还应掌握复合函数、反函数及隐函数的求导方法.
1.复合函数求导
设函数u=φ(x)在点x处可导,函数y=f(u)在点u=φ(x)处可导,则y=f(u)与u=φ(x)的复合函数y=f(φ(x))在点x处可导,且
2.反函数求导
设函数x=φ(y)在某个区间内单调可导,且φ′(y)≠0,则它的反函数y=f(x)在对应区间内也可导,且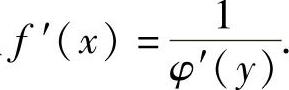
3.隐函数求导
设y=y(x)是由方程F(x,y)=0确定的隐函数,则所给方程两边对x求导(注意此时y
是x的函数)得到以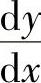 为未知数的方程,解此方程即得
为未知数的方程,解此方程即得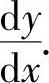
【典型例题】
例1.10.1 设函数f(x)=esinx,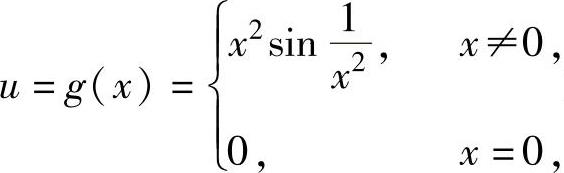 求
求
精解由复合函数求导法则得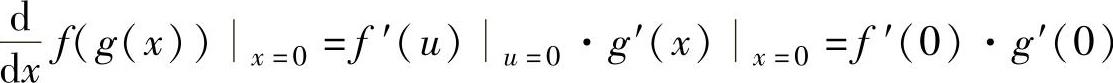 ,(1)
,(1)
其中,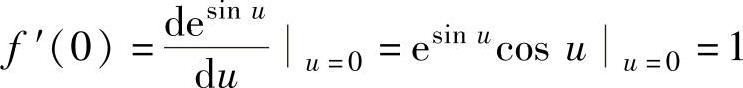 ,
,
将它们代入式(1)得
例1.10.2 求函数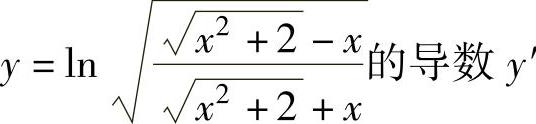 .(https://www.chuimin.cn)
.(https://www.chuimin.cn)
精解 先化简函数的表达式(例如,将真数的开方转换成对数的系数,将真数的分母有
理化),再求导.
由于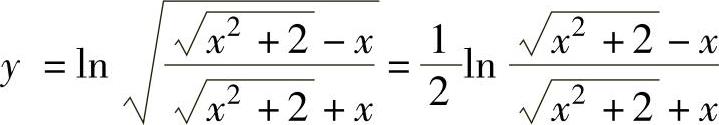
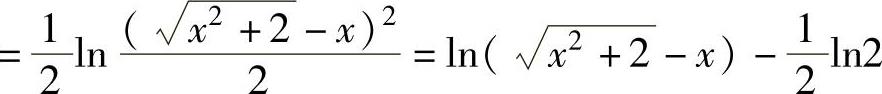 ,
,
所以,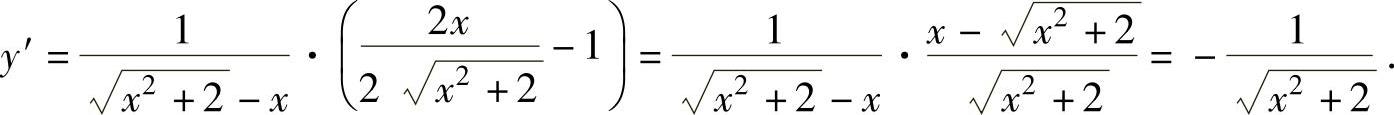
例1.10.3 设函数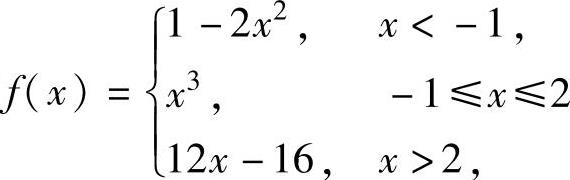 ,求y=f(x)的反函数y=φ(x)的导数φ′(x).
,求y=f(x)的反函数y=φ(x)的导数φ′(x).
精解 先确定φ(x)的表达式,然后计算φ′(x).
从y=f(x)中解出x得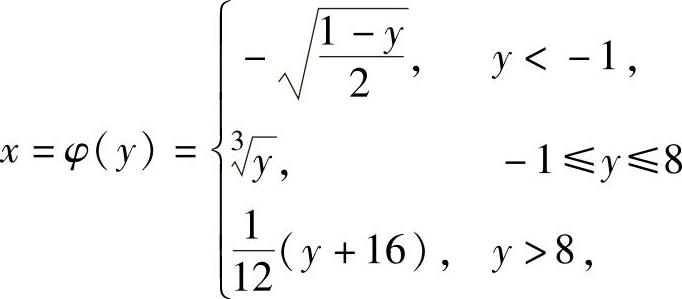 ,
,
所以y=f(x)的反函数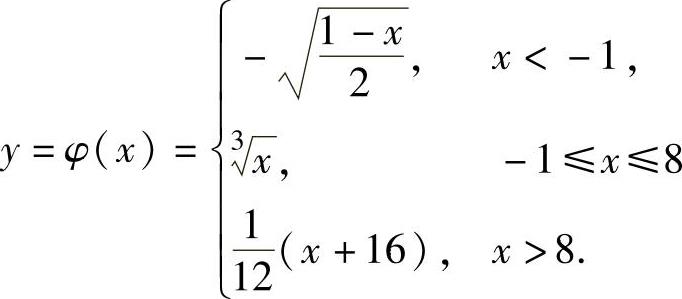 ,
,
当x<-1时,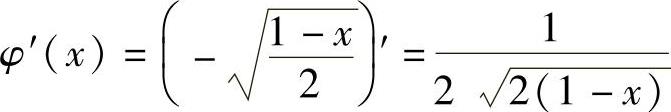 ;
;
当-1<x<8,但x≠0时,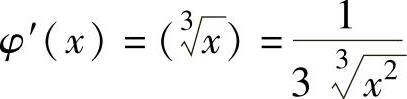 ;
;
当x>8时,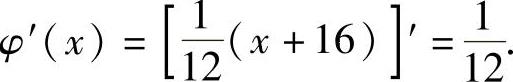
此外,由导数定义知,φ(x)在点x=-1,0处不可导,在点x=8处可导,且φ′(8)=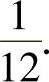
因此,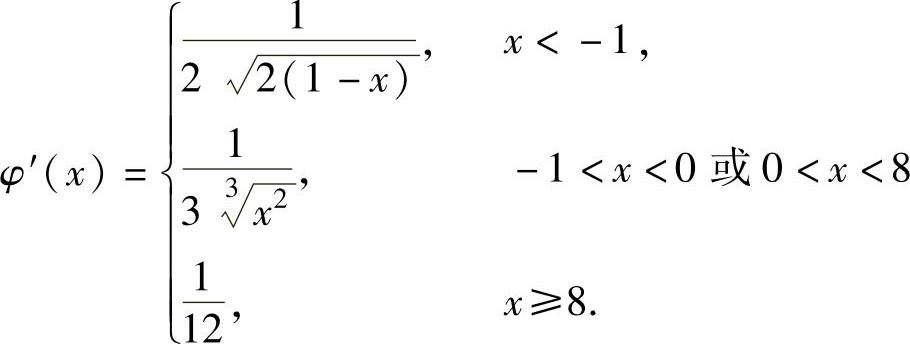 ,
,
注 在解题过程中不仅要注意φ(x)在点x=-1,8(分段点)处的可导性,还应注意φ(x)在点x=0处不可导.
例1.10.4 设函数y=f(x)由方程e2x+y-cos(xy)=e-1确定.求曲线y=f(x)在点(0,
1)处的切线方程.
精解 由隐函数求导方法算出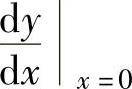 ,即可得到所求的切线方程.
,即可得到所求的切线方程.
所给方程两边对x求导得
将x=0,y=1代入上式得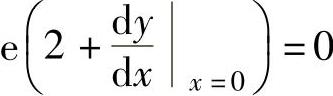 ,即
,即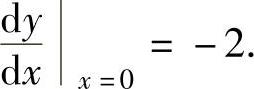
于是,曲线y=f(x)在点(0,1)处的切线方程为y-1=-2(x-0),即 y=-2x+1.
例1.10.5 求函数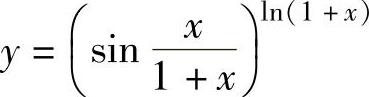 的导数.
的导数.
精解 当函数y=y(x)是幂指函数或由多个因子的积、商、乘方及开方组成时,往往采用取对数求导,即对y=y(x)的两边取对数后再求导.
所给函数是幂指函数,对其取对数得
两边对x求导得
所以,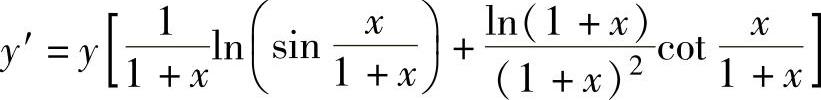
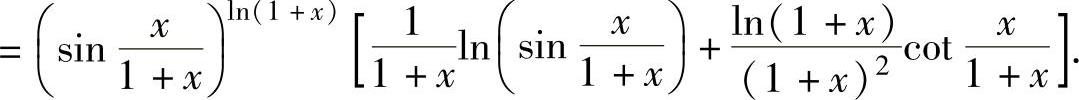
注 当y=y(x)时,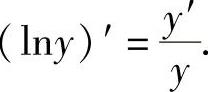 应记住这个公式.
应记住这个公式.
相关文章

定理1 如果函数u=φ(t)及v=ψ(t)都在点t可导,函数z=f(u,v)在对应点(u,v)处具有连续偏导数,则复合函数z=f[φ(t),ψ(t)]在点t处可导,且其导数可用下列公式计算定理1可推广到复合函数的中间变量多于两个的情形.例如,设z=f(u,v,ω),u=φ(t),v=ψ(t),w=ω(t)复合而得复合函数则在与定理相类似的条件下,复合函数在点t可导,且其导数可用下列公式计算式(8.......
2025-09-30

续表考点:导数在研究函数中的应用(2017全国I,21)已知函数f(x)=ae2x+(a-2)ex-x.(1)讨论f(x)的单调性;(2)若f(x)有两个零点,求a的取值范围.1.(2017山东莱芜二模)已知函数f(x)=ex[x2+(a+1)x+2a-1].(1)当a=-1时,求函数f(x)的单调区间;(2)若关于x的不等式f(x)≤ea在[a,+∞)上有解,求实数a的取值范围;(3)若曲线y=......
2025-09-30

下面将隐函数存在定理推广到方程组的情形.例如,考虑方程组这时,在四个变量中,一般只能有两个变量独立变化,因此方程组(8.5.4)就有可能确定两个二元函数.可以由函数F、G的性质来断定由方程组(8.5.4)所确定的两个二元函数的存在性以及它们的性质.我们有下面的定理.隐函数存在定理3 设F(x,y,u,v)、G(x,y,u,v)在点P(x0,y0,u0,v0)的某一邻域内具有对各个变量的连续偏导数,......
2025-09-30

基于系统分析的需要,下面介绍一些传递函数的概念。在图2-20中,将反馈环节H的输出端断开,则前向通道传递函数与反馈通道传递函数的乘积G1G2H称为系统的开环传递函数,相当于B/E。因此有5.闭环系统的误差传递函数误差大小直接反映了系统的控制精度。令n=0,则可由图2-20转化得到的图2-23求得n作用下闭环系统的扰动误差传递函数Φen。......
2025-09-29

续表考点1:函数1.(2017全国I,5)函数f(x)在(-∞,+∞)上单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是().A.[-2,2]B.[-1,1]C.[0,4]D.[1,3]考点2:对数函数2.(2017全国I,11)设x,y,z为正数,且2x=3y=5z,则().A.2x<3y<5zB.5z<2x<3yC.3y<5z<2xD......
2025-09-30

递归函数是指一个函数在它的函数体内,直接或间接地调用自己,也称为函数的递归调用。为了防止递归调用无终止地进行,在函数内必须有终止递归调用的手段。递归算法就是包含有调用算法本身语句的算法。而递归必须逐步有规律简化,最终有一个出口。应有使递归结束的条件。有5 个学生坐在一起。图5.13递归函数的执行过程用函数递归方法以字符串形式输出一个整数。......
2025-09-30

Excel 2016共提供了九大类、300多个函数,包括数学与三角函数、统计函数、数据库函数、逻辑函数等。图10-23“插入函数”对话框在“选择类别”下拉列表中选择“常用函数”选项,在“选择函数”列表框中选择“SUM”选项,单击“确定”按钮,弹出“函数参数”对话框,如图10-24所示。......
2025-09-30
相关推荐