首页理论教育《导数的几何意义及其应用》

《导数的几何意义及其应用》

2023-10-27 理论教育版权反馈

【摘要】：【主要内容】设函数f（x）在点x0处可导，则f′（x0）是曲线y=f（x）在点（x0，y0）（y0=f（x0））处切线的斜率.曲线y=f（x）在点（x0，y0）处的切线方程为y-y0=f′（x0）（x-x0）.当f′（x0）≠0时，曲线y=f（x）在点（x0，y0）处的法线方程为注（ⅰ）如果f′（x0）=∞，则曲线y=f（x）在点（x0，y0）处的切线方程为x=x0；如果f′（x0）=0，则曲线

【主要内容】

设函数f（x）在点x₀处可导，则f′（x₀）是曲线y=f（x）在点（x₀，y₀）（y₀=f（x₀））处切线的斜率.

曲线y=f（x）在点（x₀，y₀）处的切线方程为

y-y₀=f′（x₀）（x-x₀）.

当f′（x₀）≠0时，曲线y=f（x）在点（x₀，y₀）处的法线方程为

注（ⅰ）如果f′（x₀）=∞，则曲线y=f（x）在点（x₀，y₀）处的切线方程为x=x₀；如果f′（x₀）=0，则曲线y=f（x）在点（x₀，y₀）处的法线方程为x=x_0.

（ⅱ）曲线y=f（x）在点（x₀，y₀）处有切线的充分必要条件是f（x）在点x₀处可导或导数为∞.

【典型例题】

例1.9.1 设函数f（x）=xⁿ（n为正整数），且曲线y=f（x）在点（1，1）处的切线与x轴交点的横坐标为ξ_n，求极限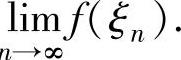

精解算出曲线y=xⁿ在点（1，1）处的切线方程以及ξ_n后即可算出极限

由于（xⁿ）′_x=1=n，所以曲线y=xⁿ在点（1，1）处的切线方程为

y-1=n（x-1），（1）

它与x轴交点的横坐标（即在式（1）中令y=0，解出的x）.

于是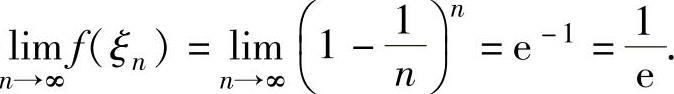

例1.9.2 设函数f（x）=（x²-x-2）x³-x，求曲线y=f（x）上不存在切线的点.

精解首先注意：函数φ（x）=x仅在点x=0处不可导，即φ′（0）不存在，但不为∞；函数xx处处可导.

于是，f（x）=（x²-x-2）x³-x=[（x-2）（x+1）x+1]xx-1仅在点x=0，1两点处不可导，即f′（0），f′（1）都不存在，但都不为∞.所以曲线y=f（x）仅在点（0，0）和点（1，0）处不存在切线.

例1.9.3 设周期为4的周期函数f（x）在（-∞，+∞）上可导，且lim

x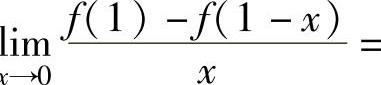(www.chuimin.cn)

，求曲线在点（5，f（5））处的法线斜率.

精解由于法线斜率为，所以只要算出f′（5）即可.

由

可知，曲线y=f（x）在点（5，f（5））的法线斜率为

例1.9.4 设曲线C：y=x³-3x²+5的切线l与直线x+9y=1垂直，求l的方程.

精解设切点为（x₀，y₀）（其中y₀=x³₀-3x²₀+5），只要算出x₀，就可确定l的方程.由于（x₀，y₀）满足

由式（2）得 x²₀-2x₀-3=0，即x₀=-1，3.将它代入式（1）对应得y₀=1，5.所以l的方程为

y-1=9（x+1）及y-5=9（x-3），即y=9x+10及y=9x-22.

注计算曲线y=f（x）的切线方程时，如果未知切点坐标，则总是设切点坐标为（x₀，f（x₀）），然后计算x_0.

例1.9.5 设两曲线y=x²+ax+b，2y=-1+xy³相切于点（1，-1），求常数a，b及公切线.

精解由于两曲线相切于点（1，-1），所以a，b应满足

相同的切线斜率，其中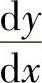，是方程2y=-1+xy³两边对x求导所得）

其中，（x²+ax+b）′_x=1=2+a，此外，方程2y=-1+xy³两边对x求导得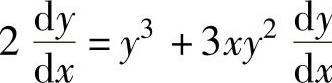y，即，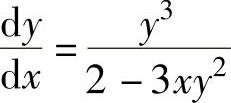

所以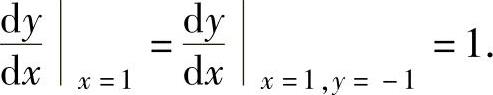

将它们代入上面所列方程组得即 a=b=-1.

并且公切线方程为

y+1=1·（x-1），即 y=x-2.