首页理论教育闭区间上连续函数的性质

闭区间上连续函数的性质

2023-10-27 理论教育版权反馈

【摘要】：【主要内容】1.最值定理设函数在[a，b]上连续，则f（x）在[a，b]上必有最大值M与最小值m，即存在ξ1，ξ2∈[a，b]，使得f（ξ1）=M，f（ξ2）=m.2.介值定理设函数f（x）在[a，b]上连续，则对介于f（x1），f（x2）（x1，x2∈[a，b]）的任意实数c，存在介于x1与x2的ξ，使得f（ξ）=c.特别地，当f（x）在[a，b]上连续，其最大值与最小值分别为M与m时，对任意c

【主要内容】

1.最值定理

设函数在[a，b]上连续，则f（x）在[a，b]上必有最大值M与最小值m，即存在ξ₁，ξ2∈[a，b]，使得f（ξ₁）=M，f（ξ₂）=m.

2.介值定理

设函数f（x）在[a，b]上连续，则对介于f（x₁），f（x₂）（x₁，x₂∈[a，b]）的任意实数c，存在介于x₁与x₂的ξ，使得f（ξ）=c.

特别地，当f（x）在[a，b]上连续，其最大值与最小值分别为M与m时，对任意c∈[m，M]，存在ξ∈[a，b]，使得f（ξ）=c.

3.零点定理

设函数f（x）在[a，b]上连续，且f（a）·f（b）<0，则存在ξ∈（a，b），使得f（ξ）=0.

零点定理有多种推广形式，例如，

（1）设函数f（x）在[a，b]上连续，且f（a）·f（b）≤0，则存在ξ∈[a，b]，使得f（ξ）=0.

（2）设函数f（x）在[a，+∞）上连续，且f（a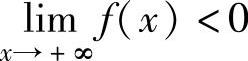）·，则存在ξ∈（a，+∞），

使得f（ξ）=0.

【典型例题】

例1.6.1 设函数f（x）在[a，b]上连续，f（a）=f（b）.证明：存在ξ∈[a，b]，使得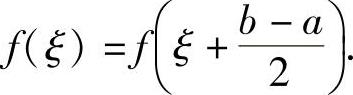

精解由于本题不是证明存在ξ，使得f（ξ）=0，而是证明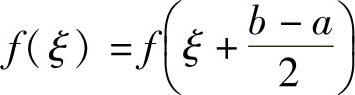，所以需(www.chuimin.cn)

要作辅助函数.它可按以下方法得到.

将欲证等式中的ξ改为x得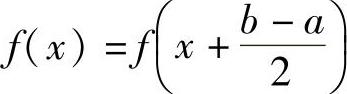，即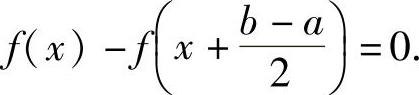

于是作辅助函数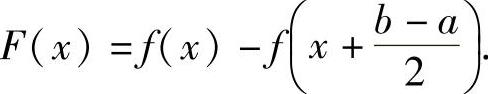具体证明如下：

记，则F（x）在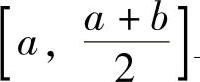上连续，且，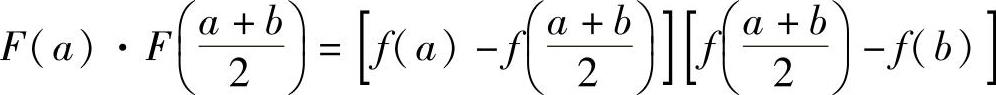

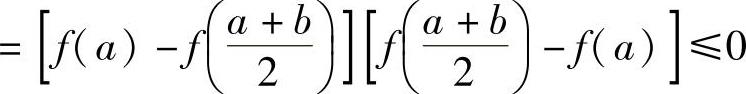所以，由连续函数零点定理（推广形式）知，存在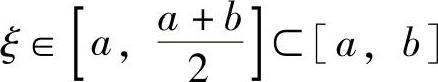，使得F（ξ）=0，即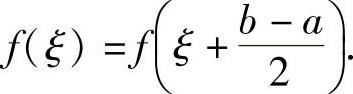

例1.6.2 证明：方程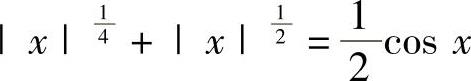有且仅有两个实根.

精解显然x=0不是方程的根.记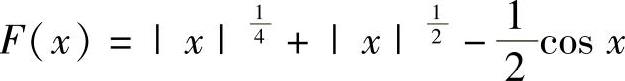，则它是连续的偶函数，于是只要证明方程F（x）=0

在（0，+∞）上有且仅有一个实根即可，故可考虑应用连续函数的零点定理（推广形式）.

容易看到，由于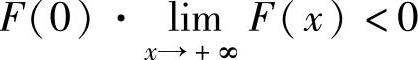，所以由连续函数零点定理（推广形式）知方程

F（x）=0在（0，+∞）上有实根.下面证明实根是唯一的.

首先，在（0，1）内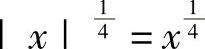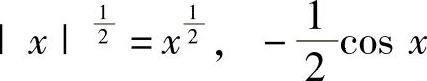，都是单调增加函数，所以F（x）

是单调增加函数，从而方程F（x）=0在（0，1）内的实根是唯一的.其次，当x≥1时，F（x）>0，即方程F（x）=0在[1，+∞）上无实根.由此得证方程F（x）=0在[0，+∞）上有唯一实根.

从而方程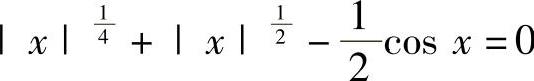有且只有两个实根.