比较和分类方法就是比较常见的哲学思维方法之一。这种对感性材料进行初步加工的方法就是比较和分类。比较和分类是科学研究中的两种基本的逻辑方法。美国杰出的政治家和科学家本杰明·富兰克林所提出的闪电和摩擦产生的电相同的见解,就是通过对闪电与电火花比较得出的。然而,富兰克林经过反覆的观察、调查和比较,却发现了它们之间存在着12个方面的共同点。......
2023-12-04
【主要内容】
1.无穷小的比较
如果
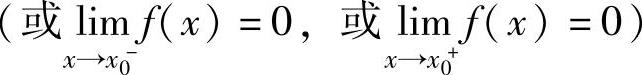 ,则称f(x)是x→x0
,则称f(x)是x→x0
 时的无穷小;
时的无穷小;
如果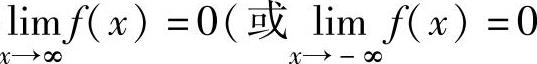 ,或
,或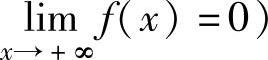 ,则称f(x)是x→∞(或x→-∞或x→+∞)时的无穷小.
,则称f(x)是x→∞(或x→-∞或x→+∞)时的无穷小.
以x→x0的情形为例叙述两个无穷小的比较:
设α(x),β(x)(其中β(x)≠0)都是x→x0时的无穷小.
如果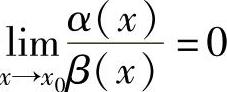 ,则称α(x)是比β(x)高阶的无穷小,记为α(x)=o(β(x));
,则称α(x)是比β(x)高阶的无穷小,记为α(x)=o(β(x));
如果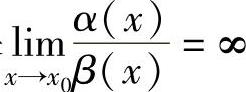 ,则称α(x)是比β(x)低阶的无穷小;
,则称α(x)是比β(x)低阶的无穷小;
如果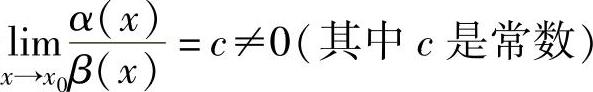 ,则称α(x)与β(x)是同阶无穷小,当β(x)=b(x-x0)k(其中b,k是常数,且b≠0,k>0),称α(x)是k阶无穷小.特别当c=1时,称α(x)与β(x)是等价无穷小,记为α(x)~β(x)(x→x0).
,则称α(x)与β(x)是同阶无穷小,当β(x)=b(x-x0)k(其中b,k是常数,且b≠0,k>0),称α(x)是k阶无穷小.特别当c=1时,称α(x)与β(x)是等价无穷小,记为α(x)~β(x)(x→x0).
2.常用等价无穷小
x→0时,以下的等价无穷小是常用的:
sinx~x,tanx~x,arcsinx~x,arctanx~x,
3.等价无穷小代替定理
设x→x0时,无穷小α(x),α1(x),β(x),β1(x)满足α(x)~α1(x),β(x)~β1(x).
如果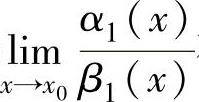 存在或为无穷大,则
存在或为无穷大,则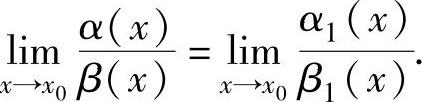
这里的x0若改为x0+,x0-,∞,+∞或-∞,上述结论仍成立.
【典型例题】
例1.3.1 (单项选择题)设当x→0时,(1-cosx)ln(1+x2)是比xsinxn高阶的无穷小,xsinxn是比ex2-1高阶的无穷小,则正整数n为().
A.1B.2C.3D.4
精解 通过寻找x→0时(1-cosx)ln(1+x2),xsinxn及ex2-1的等价无穷小即可算得n的值.
因为当x→0时
所以,由题设知 4>n+1>2,即n=2,因此选项B是正确的.(www.chuimin.cn)
例1.3.2 求极限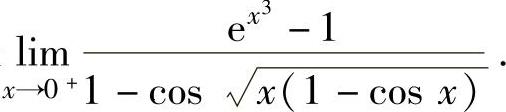
精解 由于x→0+时,
ex3-1~x3,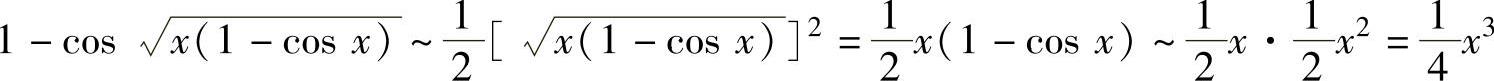 ,
,
所以,
例1.3.3 求极限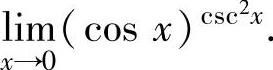
精解 利用公式Ab=eblnA得
(cosx)csc2x=ecsc2xlncosx,
然后计算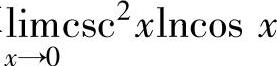 即可.
即可.
由于
 ,
,
所以, 尢
尢
注 应记住公式Ab=eblnA,它可将幂函数转换成指数函数.
例1.3.4 求极限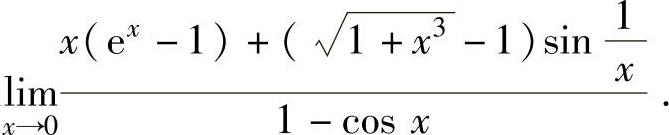
精解

其中,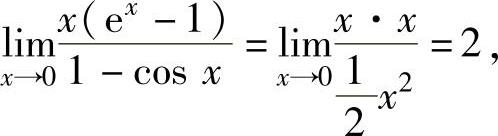
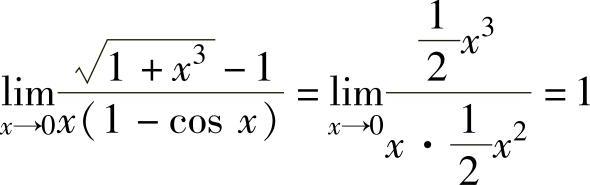 ,
,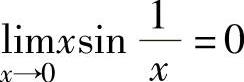 (利用无穷小的性质:设x→x0时,α(x)是无穷小,β(x)在点x0的某个
(利用无穷小的性质:设x→x0时,α(x)是无穷小,β(x)在点x0的某个
去心邻域内有界,则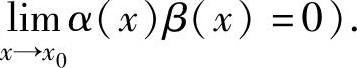
将它们代入式(1)得
例1.3.5 设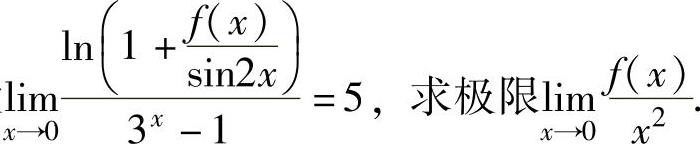
精解 由题设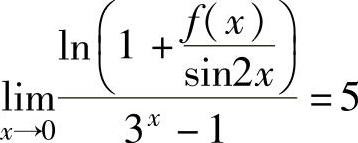 (1)
(1)
得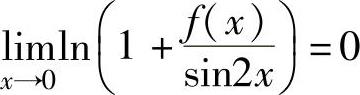 ,即
,即 ,并且
,并且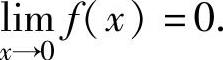
于是由式(1)得
因此,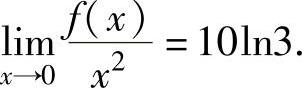
有关2015考研数学(三)基础篇全面复习与常考知识点解析的文章

比较和分类方法就是比较常见的哲学思维方法之一。这种对感性材料进行初步加工的方法就是比较和分类。比较和分类是科学研究中的两种基本的逻辑方法。美国杰出的政治家和科学家本杰明·富兰克林所提出的闪电和摩擦产生的电相同的见解,就是通过对闪电与电火花比较得出的。然而,富兰克林经过反覆的观察、调查和比较,却发现了它们之间存在着12个方面的共同点。......
2023-12-04

我们已经知道两个无穷小量的和、差、积仍为无穷小,但两个无穷小量的商的情形就较为复杂,例如下面几个简单的无穷小量的商的极限:从上面三个极限中就看出:虽然当x→0时,x3,x2,x,1-cosx都是无穷小,但它们比值的极限却有着各自不同的情形,分析这些情形产生的原因,发现是由于各个无穷小趋于零的快慢程度不同而造成的.就上面的例子来说,在x→0的过程中,x2→0的速度比x→0要快,x2→0的速度比x3→......
2023-11-19

汽车用发动机是热力机的一种。热力机的运行原理根据其热效果的不同而有所差异。热力机就是通过热能的传递使流体发生膨胀和收缩,把热能转换成机械能的装置。外燃机的燃烧气体与工质流体不是同一种气体,且产生热量的部分和发生动力的部分各自独立。根据工质流体转换为功的方式不同,热力机可分为往复型和旋转型。表1-1 热力机的分类和比较......
2023-06-28

铸造工艺按铸型材料、造型工艺和浇注方式不同,可分为砂型铸造和特种铸造两大类。砂型铸造砂型铸造是将液态金属浇注到预制的型腔中,待金属冷凝后获得铸件(毛坯)的方法。砂型铸造应用较广泛,既适用于单件、小批量的手工造型,也适用于批量生产的机器造型和自动生产线。表5.1几种主要铸造方法的比较......
2023-06-27

按带的横剖面形状是矩形、梯形和圆形,带可分为: 平型带[图4-2( a)]、三角带[图4-2( b)]和圆型带[图4-2( c)]。本章着重讨论三角带传动。沿三角胶带中性层 量得的周长称为节线长度L,用于带传动的几何尺寸计算。 带传动的外廓尺寸较大。 传动效率较低,三角带传动的效率一般为η=0.90 ~0.94。此外,带传动由于存在摩擦会产生电火花,故不能用于可能发生爆炸的场合。三角带传动的传动比一般为i≤7,少数可达10。......
2023-06-16

一、无穷小(一)定义1若lim x→x0f(x)=0,则称函数f(x)是x→x0时的无穷小量(或无穷小).注:无穷小是对一个函数而言的,是一个动态的变量.无穷小量、无穷小量的概念是反映变量的变化趋势,因此任何常量都不是无穷小量,任何非零常量都不是无穷小,在谈及无穷小量、无穷小量之时,首先应给出自变量的变化趋势.(二)性质定理1有限个无穷小的和也是无穷小.定理2常数与无穷小的乘积是无穷小.定理......
2023-11-20

插图应与论文的内容密切相关,应能协助读者理解论文的主旨和研究结果。我们以论文实例2中的Fig.2和一篇报道新型固液相变太阳能热储存材料与技术的论文中[8]的Fig.3为例,来说明设计和作图的注意点。饼状图主要用于研究对象的统计分析,显示其各组分的含量关系。图6-3 饼图,显示2009年各国已经承诺的对绿色环保所作的投入[9]2.线图例如机械图、电气图、流程图、示意图等。......
2023-07-08

在航空法中,航空器一般分为“民用航空器”和“国家航空器”两类,其用途、性质和法律地位均有区别。这实质上牵涉到把握有关区分国家航空器和民用航空器概念标准的分歧。他们认为,凡是用于国家司法行政事务、军事、海关和警察安全部门的航空器,均属于国家航空器;国家航空器之外的其他航空器为民用航空器。国家航空器之外的其他用于商业目的或私人目的航空器则可归入民用航空器之列。......
2023-07-24
相关推荐