首页理论教育函数极限与左、右极限关系

函数极限与左、右极限关系

2023-10-27 理论教育版权反馈

【摘要】：【主要内容】1.设函数f（x）在点x0的某个去心邻域内有定义，则limx的充分必要条件是注（ⅰ）对任意ε>0，如果存在δ>0，当0<|x-x0|<δ时有|f（x）-A|<ε.对任意ε>0，存在δ>0，使得-δ0，存在δ>0，使得0

【主要内容】

1.设函数f（x）在点x₀的某个去心邻域内有定义，则lim

x的充分必要条件是

注（ⅰ）对任意ε>0，如果存在δ>0，当0<|x-x₀|<δ时有

|f（x）-A|<ε.对任意ε>0，存在δ>0，使得-δ<x-x₀<0时有|f（x）-A|<ε.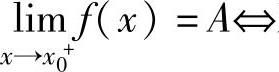对任意ε>0，存在δ>0，使得0<x-x₀<δ时有|f（x）-A|<ε.

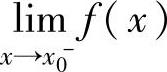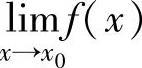（ⅱ）当x₀是分段函数f（x）的分段点时，总是通过计算其左极限和右极限来确定是否存在.

2.设f（x）在|x|>N（N是某个正数）内有定义，则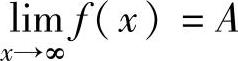的充分必要条件是.

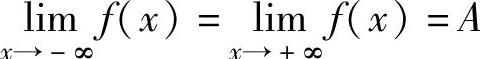注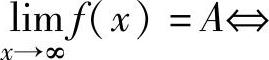对任意ε>0，存在G>0，使得|x|>G时有|f（x）-A|<ε.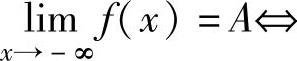对任意ε>0，存在G>0，使得x<-G时有|f（x）-A|<ε.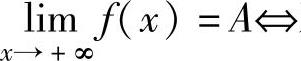对任意ε>0，存在G>0，使得x>G时有|f（x）-A|<ε.

【典型例题】

例1.1.1 设函数f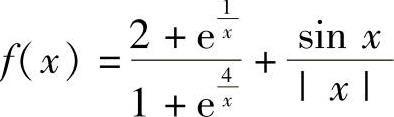，求极限lim_x→0f（x）.

精解由于

是分段函数，所以计算它在分段点x=0处的极限应从计算左极限与右极限入手.(www.chuimin.cn)

由于，，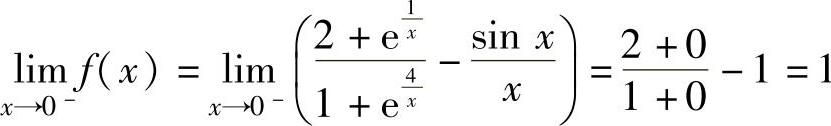

所以，.

注应注意，.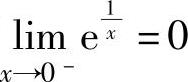

例1.1.2 确定使极限存在的常数a的值，其中

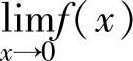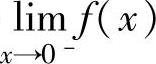精解由存在可得和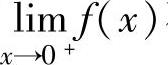存在且相等，由此即可算出a的值.

由于，，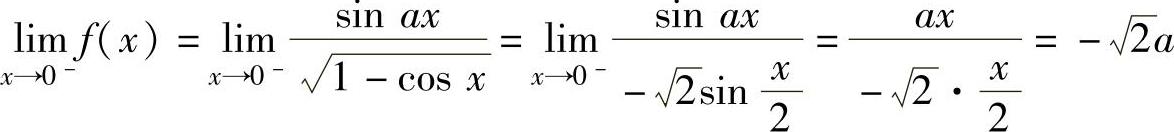

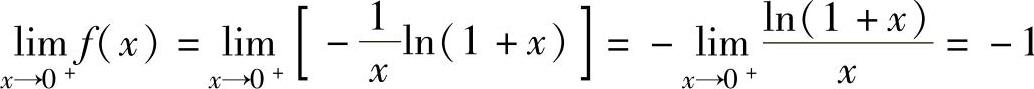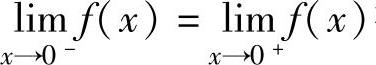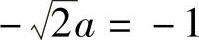所以，由得，即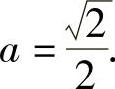

例1.1.3 求极限

精解由于x→∞时，x-1与4x²相比可忽略不计，同样1与x相比可忽略不计，sinx与x²相比可忽略不计.于是，

其中，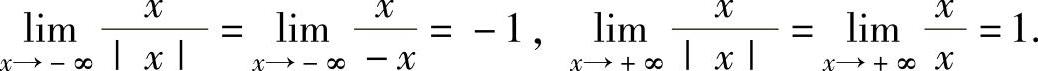

所以，极限不存在.