【摘要】:一个典型单元的运动方程可以由能量表达式推导出。描述全部系统的运动方程通过装配单元矩阵和向量而得到。对一个齿轮传动系统,每个分支的运动方程必须参考轴1(参考轴),而惯量、阻尼和刚度矩阵必须乘以n2,载荷向量必须乘以n。表15-1 齿轮轴系实际系统和等效系统的转换关系装配后的运动方程为:从模态质量和阻尼方程,得到:在实际应用时,保留模态数(N^)远远小于系统所有的模态数N。
对纯扭转振动,每个有限单元的运动都可以由绕旋转轴的转动位移坐标θ来表示。一个典型的轴段单元有两个自由度(每端一个自由度)。如图15-6所示,在位置l的自由度用θ(l,t)表示。一个典型单元的运动方程可以由能量表达式推导出。

图15-6 扭转自由度示意图
对一个有各向同性材料的典型单元,动能和势能为:
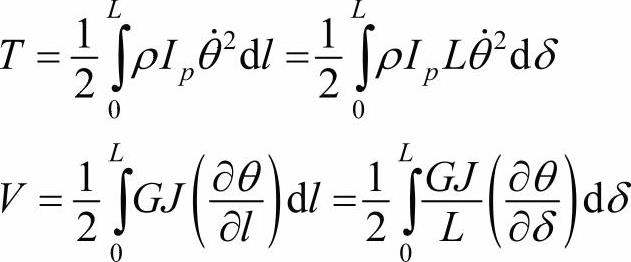
其中,ρ是密度,G是剪切模量,也是绕中心轴的极转动惯量,J是截面的几何特性。对圆截面来说,J=Ip对其他截面形状,J<Ip。读者可以从文献中获得J的表达式。局部坐标l是从0到L,局部非尺寸坐标是从0到1。在单元内的旋转位移坐标可以近似用两端的转动位移和形函数来表示:
θ(l,t)=N1(l)θ1(t)+N2(l)θ2(t)
线性形函数可以用两个端点的边界条件来获得:
θ(0,t)=θ1(t)
θ(L,t)=θ2(t)
线性形状函数为:
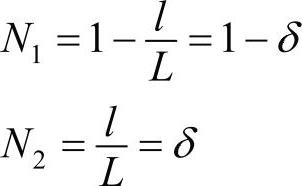
将转动位移方程代入能量表达式:
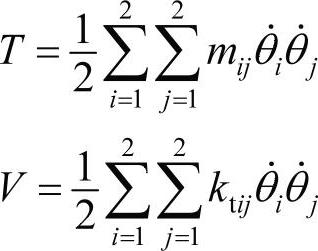
刚度和质量系数为:
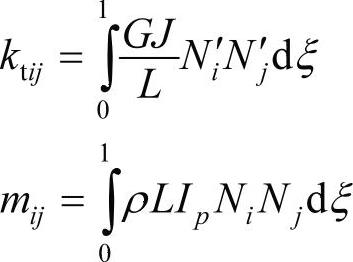
广义力(力矩)从外力虚功获得:
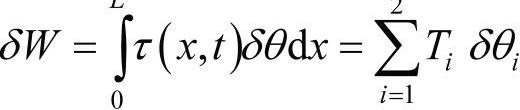
广义力矩为:
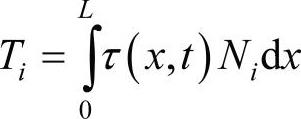 (www.chuimin.cn)
(www.chuimin.cn)
注意到符号T也用来表示力矩,它与动能符号不是一回事。
对锥形单元,圆截面(J=Ip)的极转动惯量用左端的特性来表示:
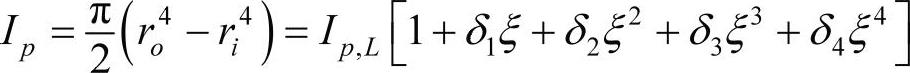
其中,Ip是单元最左端的极转动惯量。

代入形状函数表达式,并对能量表达式积分,得到:
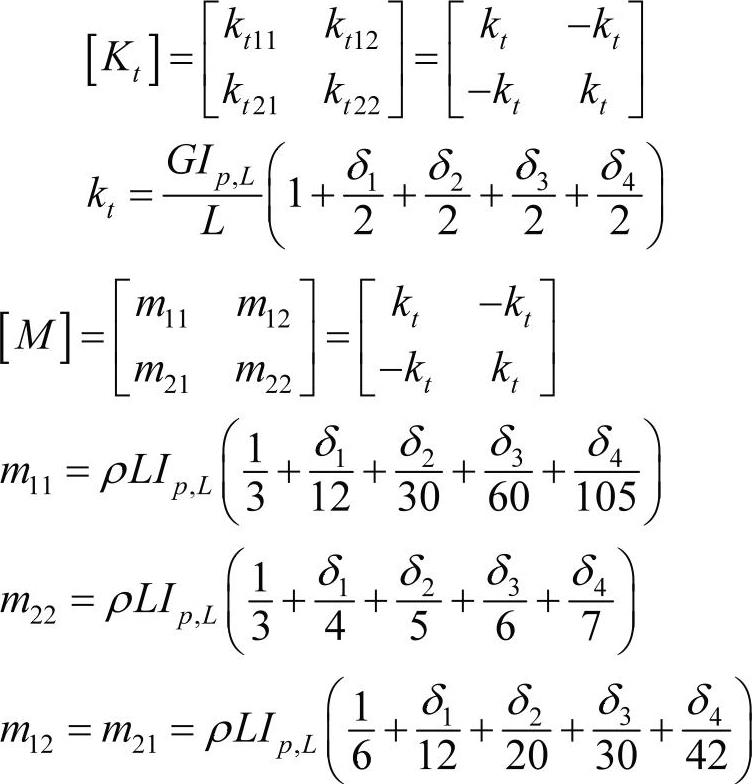
对圆柱单元,由于左端和右端的特性是相同的,因此矩阵简化为更熟悉的形式:
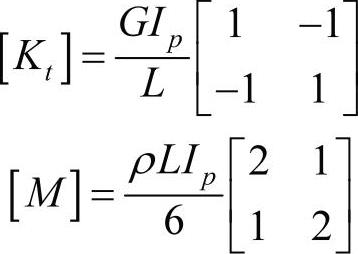
利用形状函数导出质量矩阵和刚度矩阵,利用形状函数导出的质量矩阵被称为“一致质量阵”。在扭转振动中,对圆柱单元来说,通常假设单元惯量是集中在单元两端的,即每个端部是一半的转动惯量。对圆柱单元,对角质量矩阵一般也称为“集中质量矩阵”,或者“集束质量矩阵”。

描述全部系统的运动方程通过装配单元矩阵和向量而得到。单元坐标必须由总体广义坐标替代。对一个齿轮传动系统,每个分支的运动方程必须参考轴1(参考轴),而惯量、阻尼和刚度矩阵必须乘以n2,载荷向量必须乘以n。这里n是分支轴相对于参考轴的转速比。表15-1是齿轮轴系实际系统和等效系统的转换关系。
表15-1 齿轮轴系实际系统和等效系统的转换关系

装配后的运动方程为:
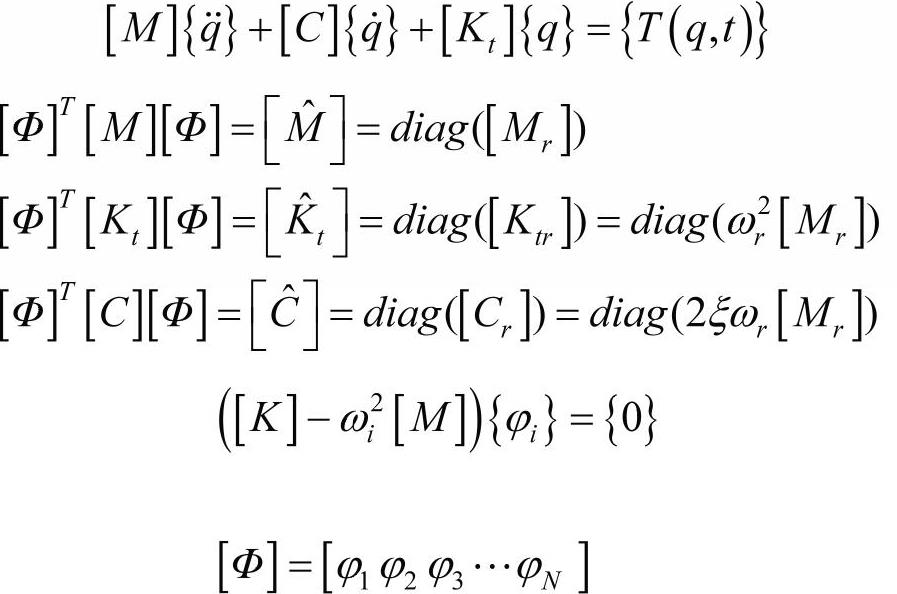
从模态质量和阻尼方程,得到:
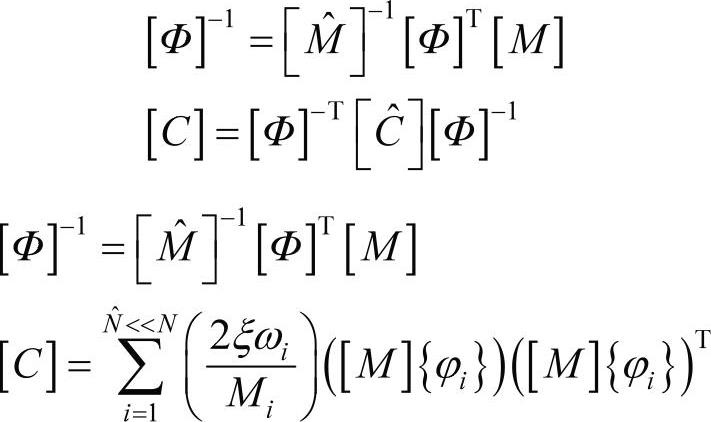
在实际应用时,保留模态数(N^)远远小于系统所有的模态数N。在扭转振动中,阻尼对固有频率的影响非常小。通常计算无阻尼固有频率,并绘制成频率转速图,即坎贝尔图(Campbell Diagram)。只有当计算强迫响应时才需要阻尼矩阵。


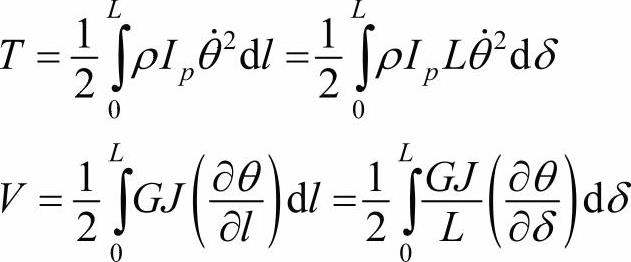
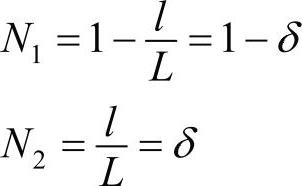
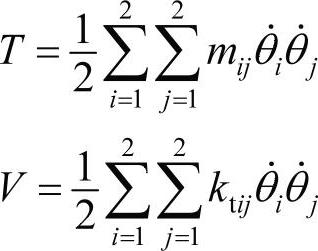
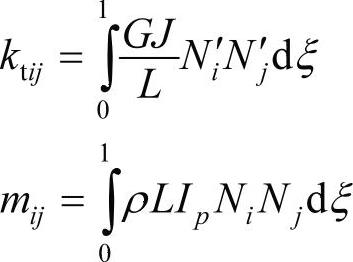
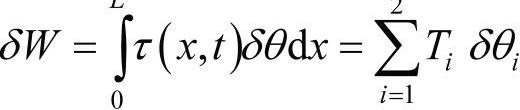
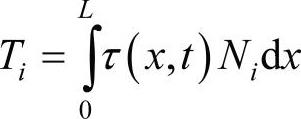 (www.chuimin.cn)
(www.chuimin.cn)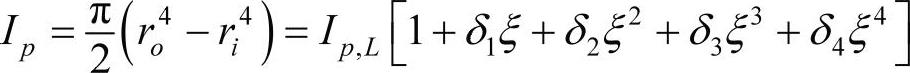

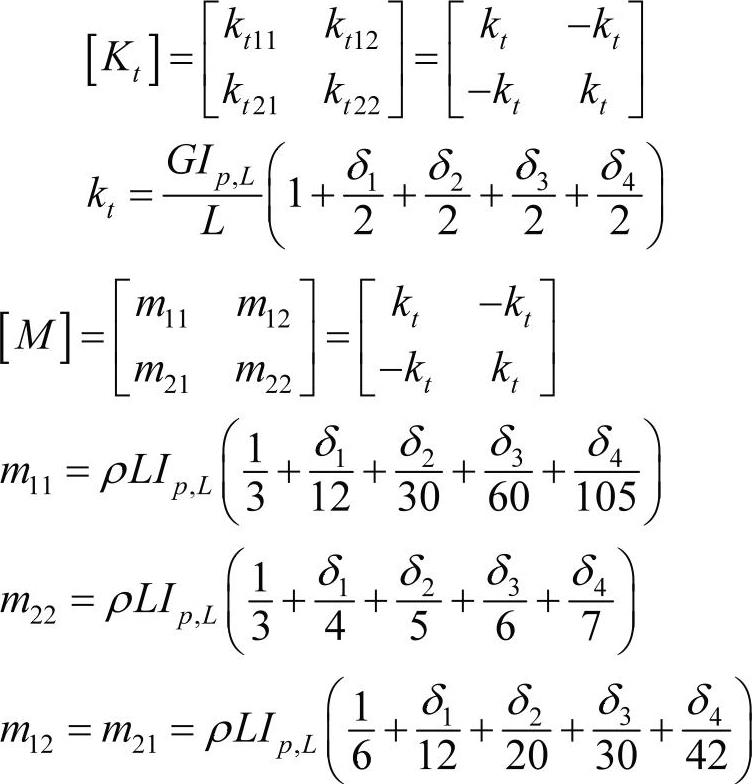
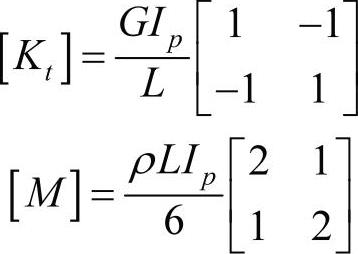


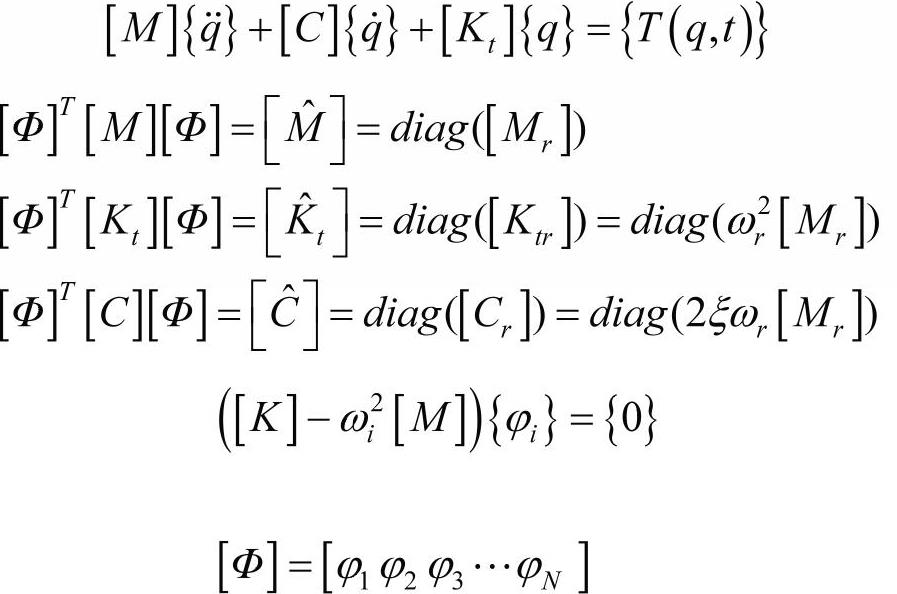
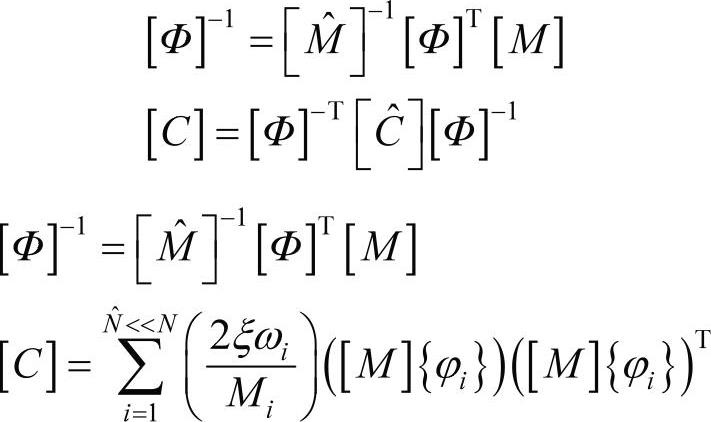






相关推荐