【摘要】:对齿轮系统,齿上的扭转刚度远小于系统的其他扭转柔性,除了齿轮上齿就可以认为是刚性连接。图15-4 最简单的齿轮系统在此例中,假设旋转坐标系的方向是相同的,不考虑轴的旋转方向。因此这个齿轮系统等效为单轴系统。q1=θ1,q2=θ2,q3=θ4/ n 或者θ1=q1,θ2=q2,θ3=nq2,θ4=nq3将上述表达式代入能量表达式,得到:和从拉格朗日方程推导出齿轮系统的运动方程:
对齿轮系统,齿上的扭转刚度远小于系统的其他扭转柔性,除了齿轮上齿就可以认为是刚性连接。考虑图15-4所示简单的齿轮系统,轴2和轴1的传动比为n。
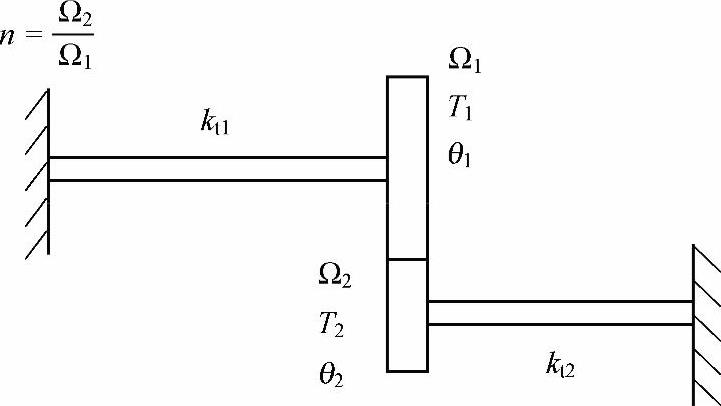
图15-4 最简单的齿轮系统
在此例中,假设旋转坐标系的方向是相同的,不考虑轴的旋转方向。外部扭矩的方向与轴旋转的方向相同。同时,此例中系统是约束的,刚体模态不存在。
系统动能和势能为:
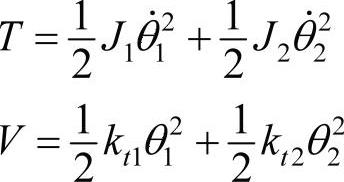
外部扭矩虚功为:
δW=T1δθ1+(-T2)δθ2
注意T2前面是负号,这是由于此例中扭矩是轴旋转的方向,它对应的转动位移θ2的负方向。此系统中有两个转动坐标,然而,这两个坐标可以通过传动比关联。全部的独立广义坐标只有一个,此系统为单自由度系统。因此这个齿轮系统等效为单轴系统。考虑轴1为参考轴,代入几何约束(θ2=-nθ1)到能量和虚功表达式中,这样得到单自由度系统:
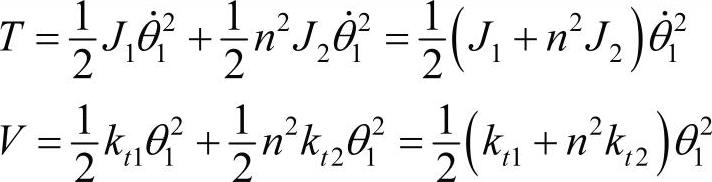
和 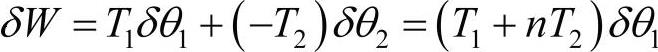
这样,轴2相对于轴1的等效惯量和扭转刚度为n2J2和n2k2。

如果以轴2为参考轴,则可以得到:
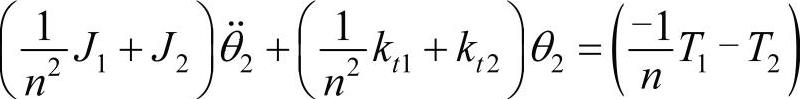
或者
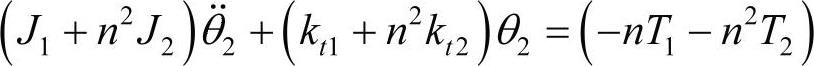
代入,以轴2为参考轴导出的上述方程,与由轴1为参考轴导出的方程是一致的。所以,选择哪个轴作为参考轴不影响计算结果。在SAMCEF Rotor软件建模时,通常使用轴1作为参考轴。
如果齿轮系统的角转动坐标与轴的转动方向相同,转动角度的几何关系变为θ2=nθ1,轴2的等效惯量和等效刚度分别为n2J2和n2k2,外力矩虚功为: 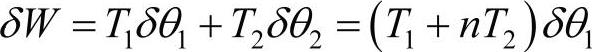 (www.chuimin.cn)
(www.chuimin.cn)
注意到此时力矩的方向与转动方向一致,等效力矩为nT2。所以,结果与前面导出的结果相同。
下面考虑一个简单的齿轮传动实例。如图15-5所示,此系统由一个电动机J1、一个大齿轮J2、一个小齿轮J3和一个风机J4组成。传动比(风机轴转速/电动机轴转速)为n。每个部件有一个集中地转动惯量,并对应一个转角位移。
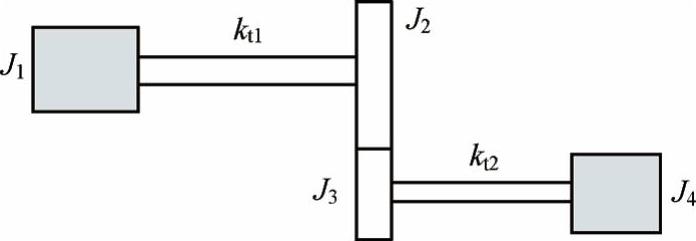
图15-5 电动机-风机系统
系统的动能和势能为:
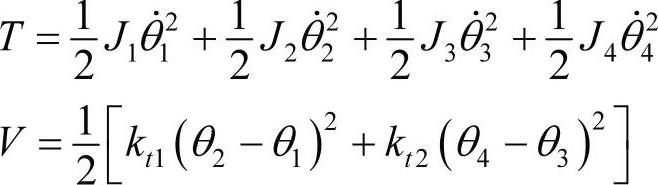
有两个外力扭矩(电机上的驱动扭矩和压缩机上的抵抗扭矩),这两个外力扭矩的虚功为:
δW=Tmδθ1+Tcδθ4
注意到在此例中选择的是角度位移,以便位移与轴旋转方向一致。尽管系统有四个物理转角坐标(每个惯量一个),而由于有一个齿轮(刚性)连接约束θ3=nθ2,因此此系统实际上是一个三自由度系统。三个独立的广义坐标为(q1,q2,q3),可以定义四个物理坐标(θ1,θ2,θ3,θ4)与之的关系。
q1=θ1,q2=θ2,q3=θ4/ n 或者
θ1=q1,θ2=q2,θ3=nq2,θ4=nq3
将上述表达式代入能量表达式,得到:
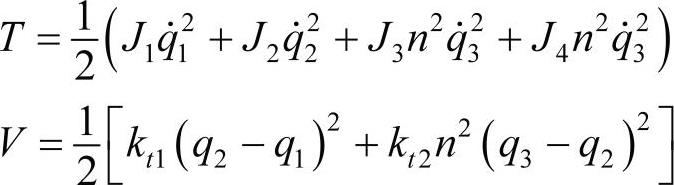
和
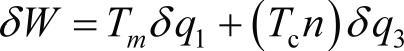
从拉格朗日方程推导出齿轮系统的运动方程:
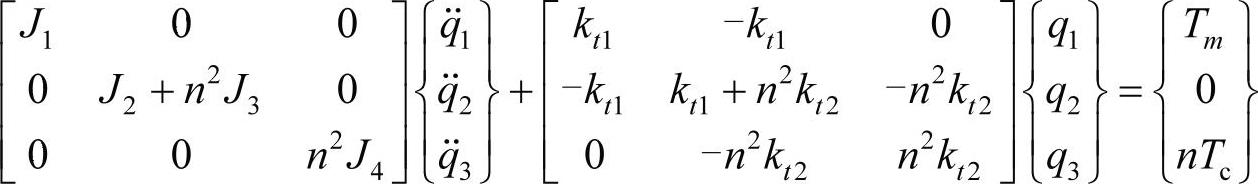


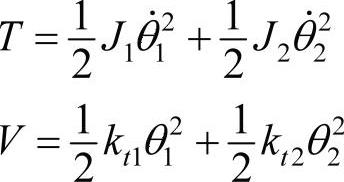
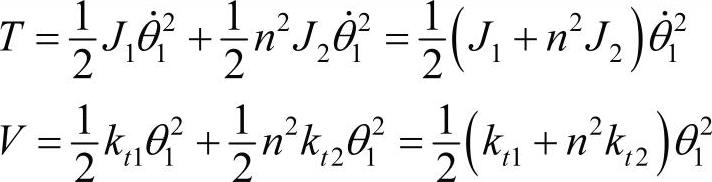
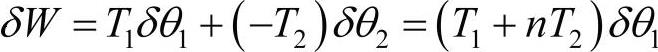

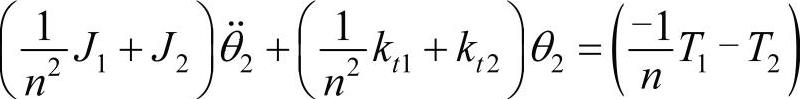
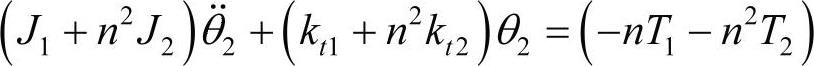
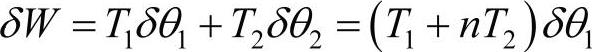 (www.chuimin.cn)
(www.chuimin.cn)
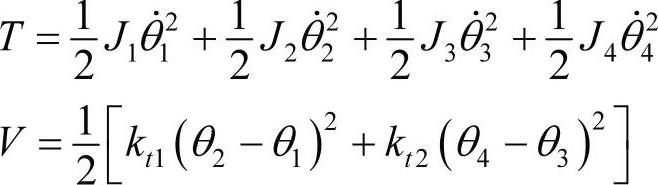
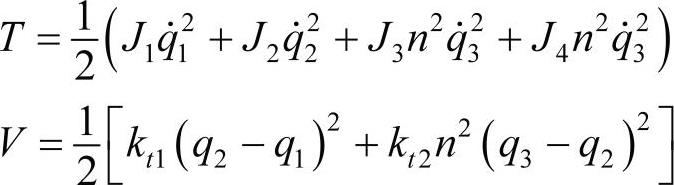
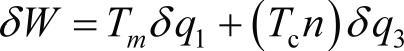
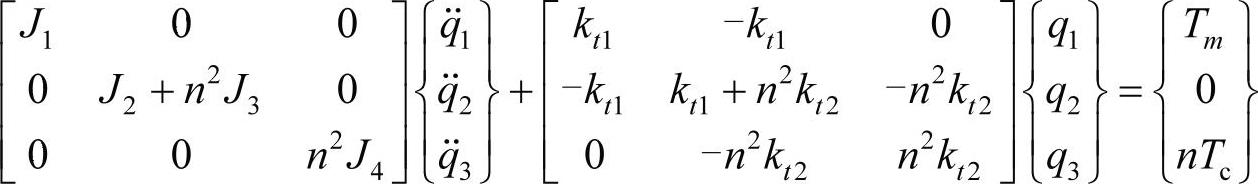







相关推荐