图14-222所示是一个悬臂盘转子。在本实例中使用SAMCEF Rotors软件中特有的二维轴对称傅立叶单元模型模拟轴，轮盘使用三维实体单元建模。此例几何模型和有限元网格已经创建完成，下面在SAMCEF Field中完成二维轴对称单元和三维实体单元的连接。
（1）启动SAMCEF Field，当出现求解器设置对话框时，在Domain下拉列表框中选择Rotor Dynamics。
（2）读取已经存在的分析模型，在菜单栏中选择File→Open命令，选择fourier_3D_disk_initial.sfield文件。读取的悬臂盘转子几何模型见图14-223。
图14-222 悬臂盘转子示意图
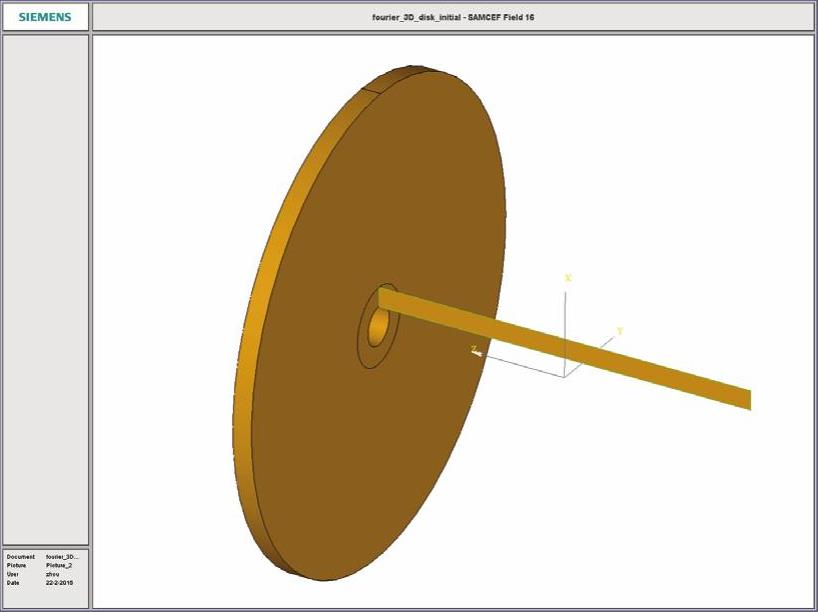
图14-223 悬臂盘转子几何模型
（3）单击
模块图标，进入分析数据模块。
（4）在数据树Mesh Model中选中网格Mesh_shaft_2D和Mesh_Gluing1，单击鼠标右键，选择Show命令，有限元网格如图14-224所示。
图14-224 悬臂盘转子有限元网格
此模型中，轴是二维网格，在径向分为2层，盘为三维网格。轴与盘连接处网格一致，即轴二维网格绕旋转轴旋转得到的三维网格与盘的网格刚好是一致的。注意网格一致是二维模型和三维模型连接的最基本要求。建议盘与轴连接位置应划分为旋转扫掠网格，这样便于连接。
(5)在数据树Mesh Model中选中网格Mesh_Gluingl，单击鼠标右键，选择Hide命令，只显示二维网格。
(6)在数据树Mesh Model中选中网格Mesh shaft 2D，单击鼠标右键，选择Mesh Aspect--Other命令，弹出图14 225所示对话框，选中Node Number复选框，编号轴网格节点编号显示出来，如图14 226所示。轴上与盘连接的三个节点按半径从小到大分别编号为12109，12110和12111。
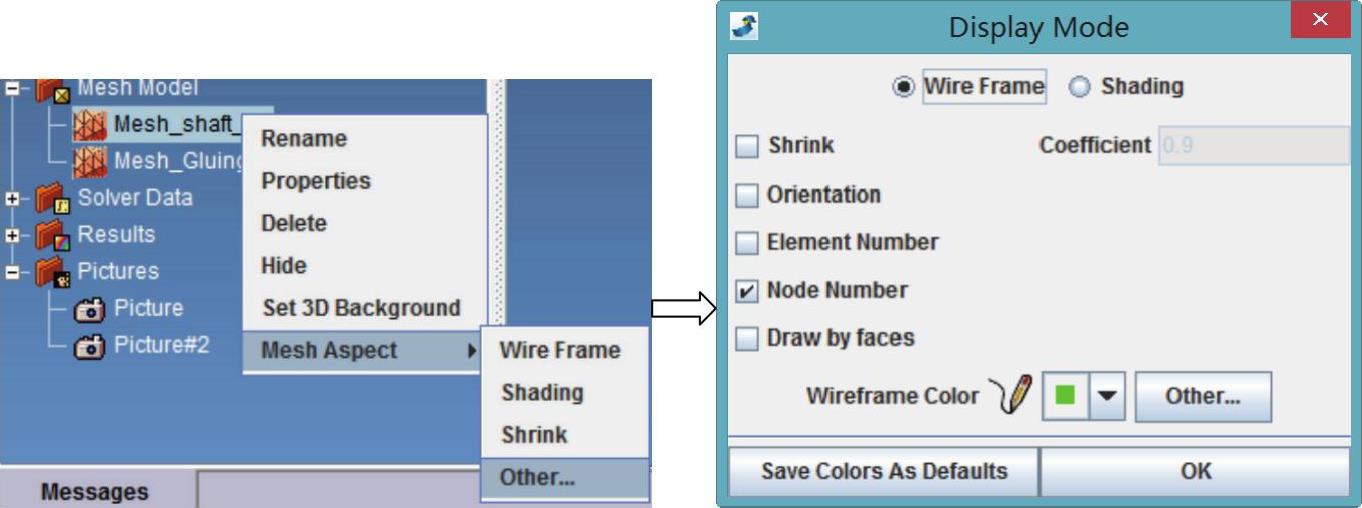
图14-225 显示节点编号设置
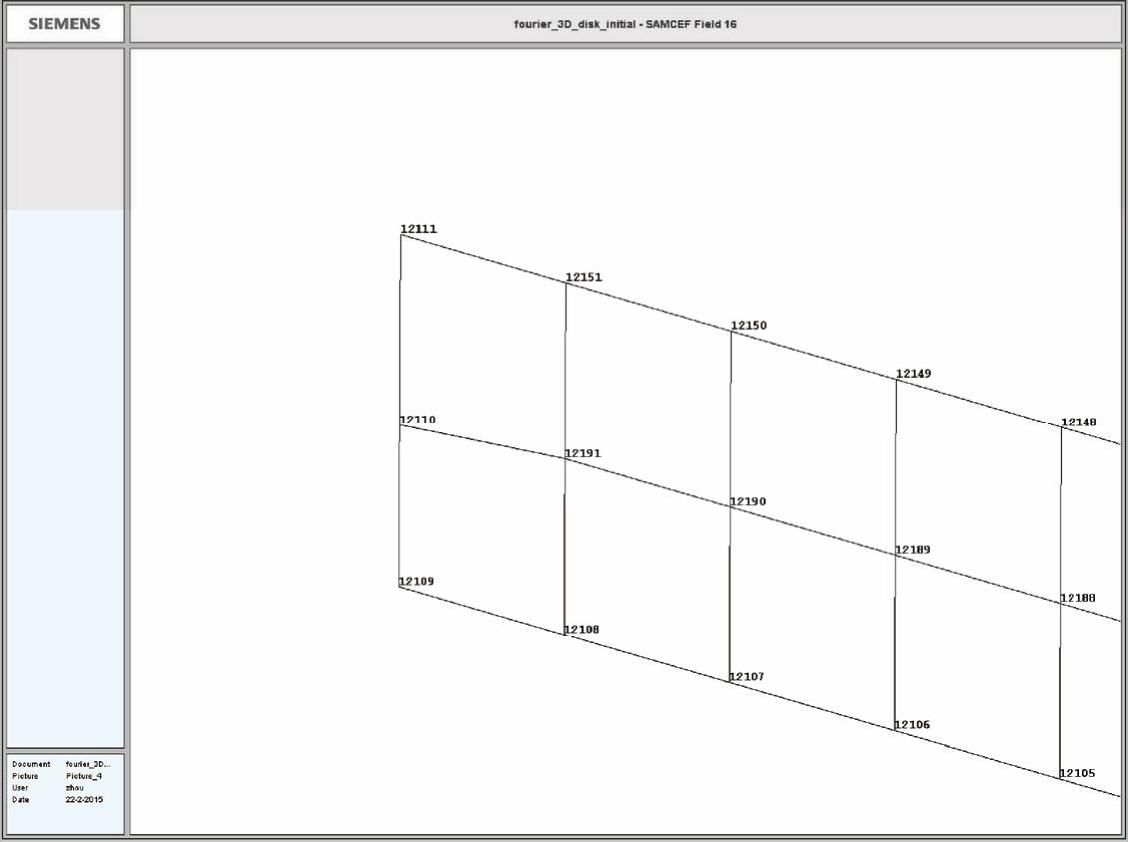
图14-226 轴网格节点编号
（7）在数据树Model下的Directory中选中网格Gluing，单击鼠标右键，在弹出菜单中选择Mesh Group命令。
（8）如图14-227所示，在Name文本框中输入节点组的名称upper_nodes，在下拉列表框中选择EDGE，在图形上选择与12111节点对应的盘上圆弧线（见图14-228），单击Apply按钮生成节点组upper_nodes，此节点组包含在这条圆弧线上的所有24个节点。
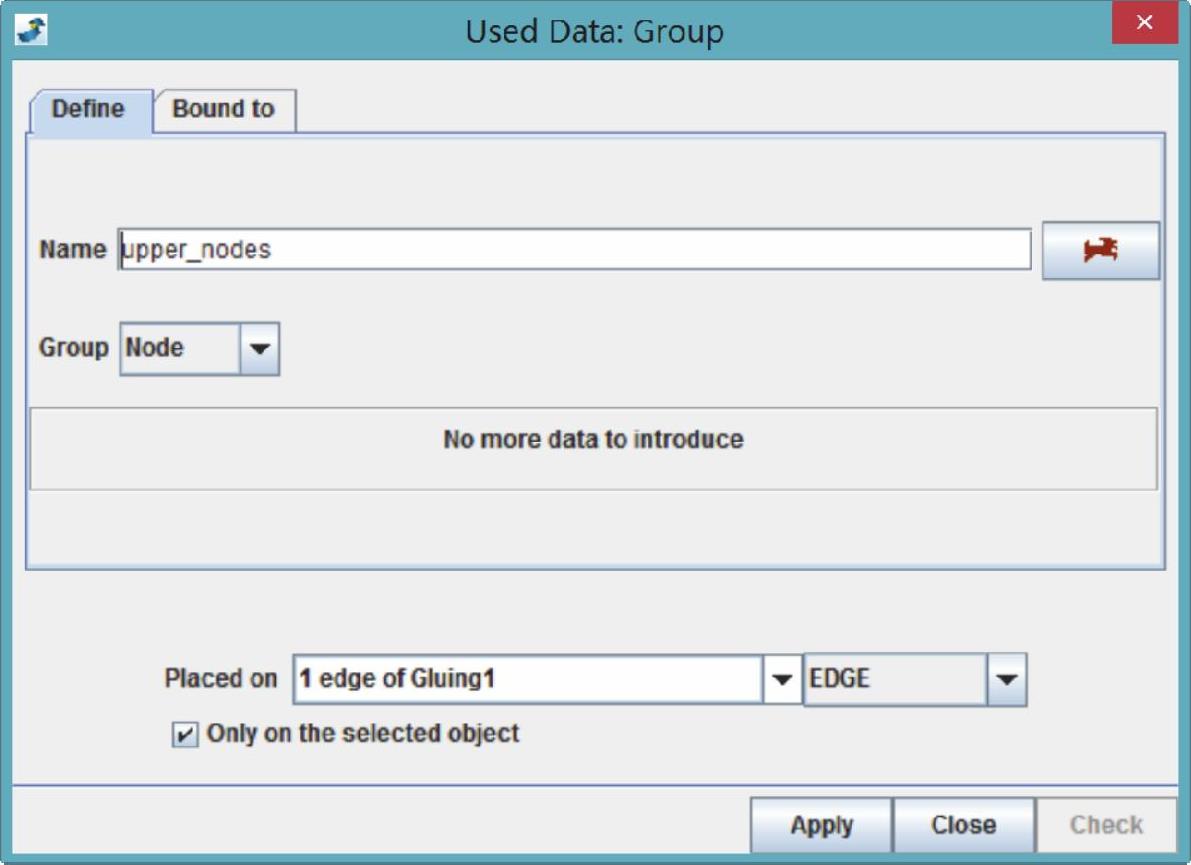
图14-227 创建组
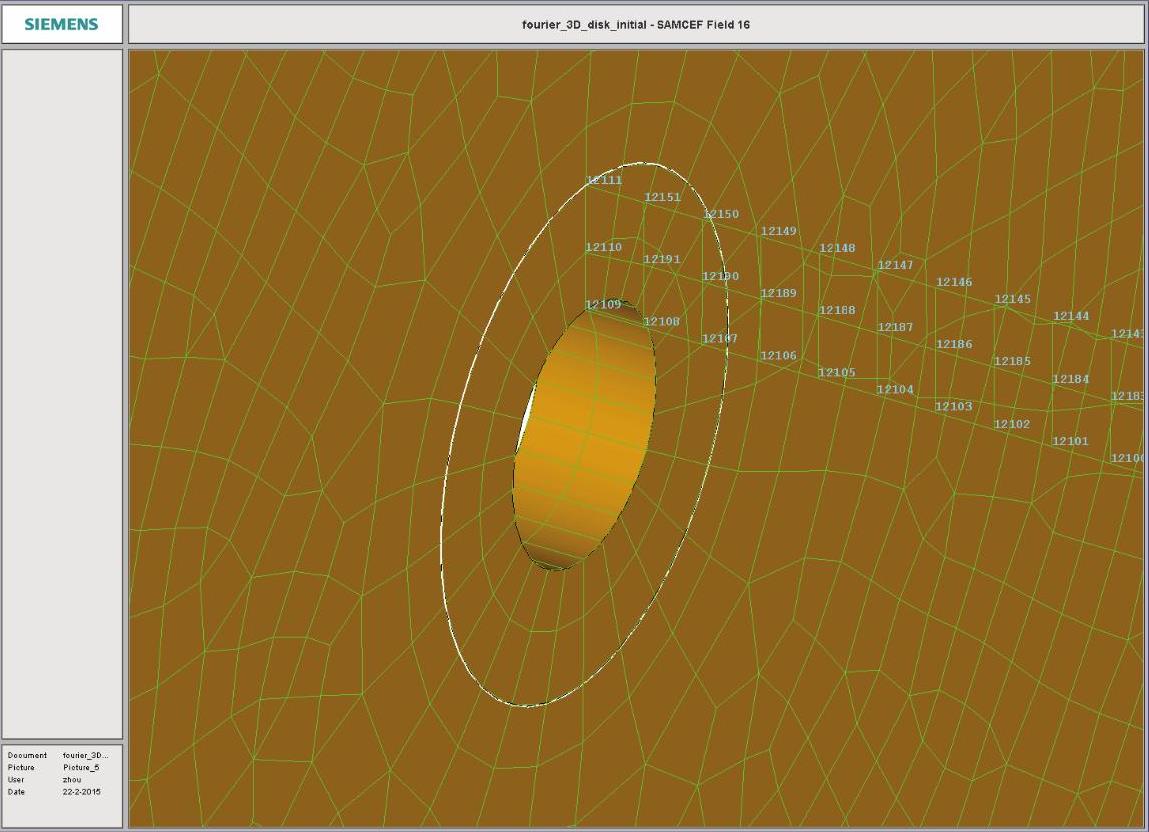
图14-228 线创建节点组
（9）重复上述过程，创建另外一个节点组lower_nodes。由于与节点12110对应的盘上的节点不在几何线上，因此生成这个节点组时用选择节点的方法，即在Group下拉列表框中选择Node，然后在图形区用鼠标拾取对应的24个节点，从而创建节点组mid_nodes。
（10）单击
模块图标，进入求解模块。再单击Epilogue按钮，打开命令行输入界面。如图14-229所示，在命令行里面输入命令：
.fc3 n 12111 Gtar"upper_nodes"
n 12110 Gtar"mid_nodes"
n 12109 Gtar"lower_nodes"
注意此命令是将二维轴上的节点与三维盘上的对应节点自由度耦合在一起。(www.chuimin.cn)
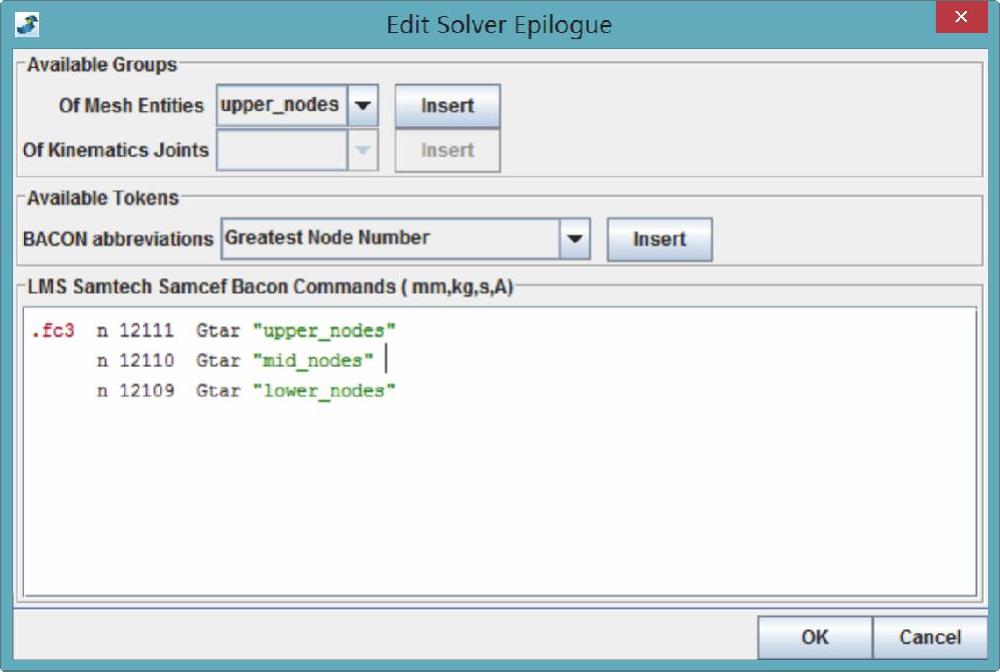
图14-229 连接命令
（11）单击
图标，在弹出的对话框中选择Eigen Values
Sweeping选项卡，设置如下：Number of Eigen Values设置为20；Algorithm选择直接法Direct。
（12）单击
图标，弹出求解监控对话框（见图14-230），并开始计算。
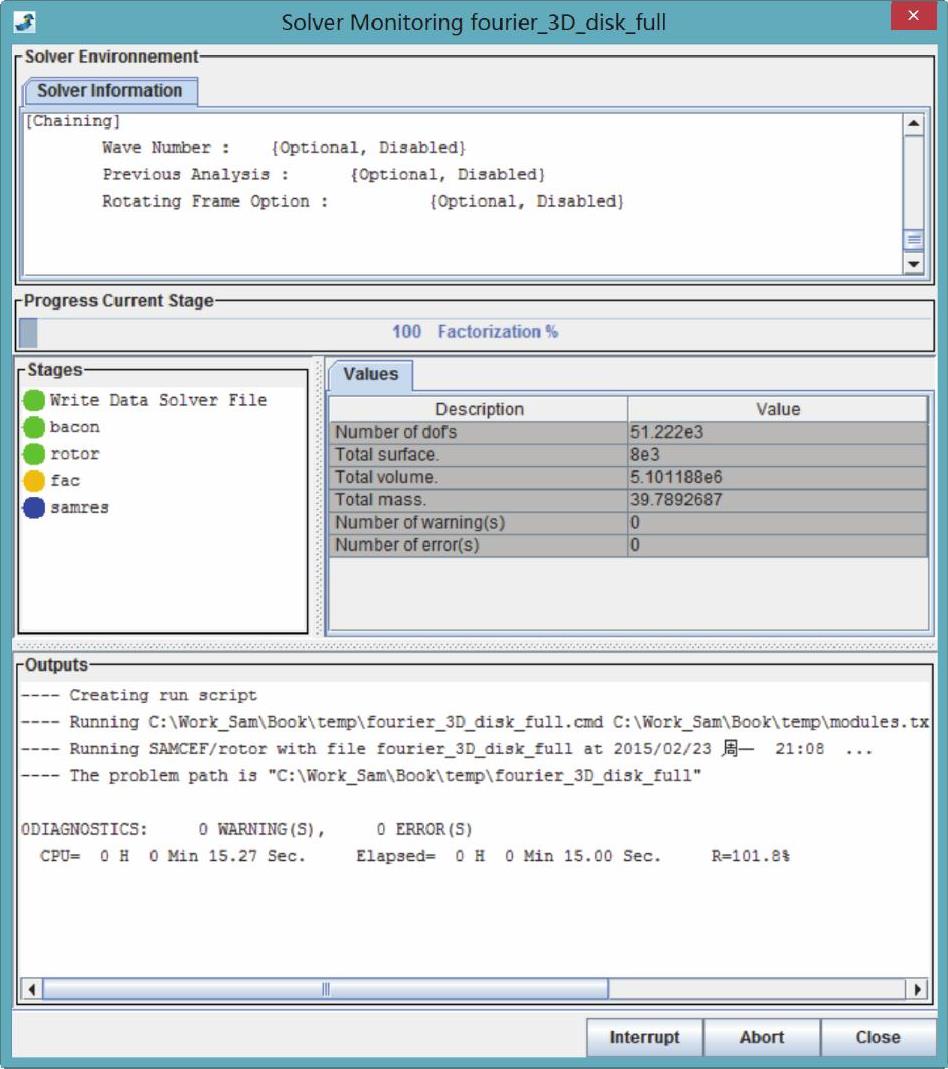
图14-230 求解器监控页面
（13）计算完成后，单击
模块图标，进入结果显示模块。
（14）在结果显示模块中显示临界转速振型，其中第1阶正向涡动临界转速振型见图14-231，耦合振动2节径第1阶振型见图14-232，耦合振动0节径第1阶振型见图15-233，第2阶正向涡动临界转速振型见图14-234。
表14-18 混合模型与整体分析模型的对比情况
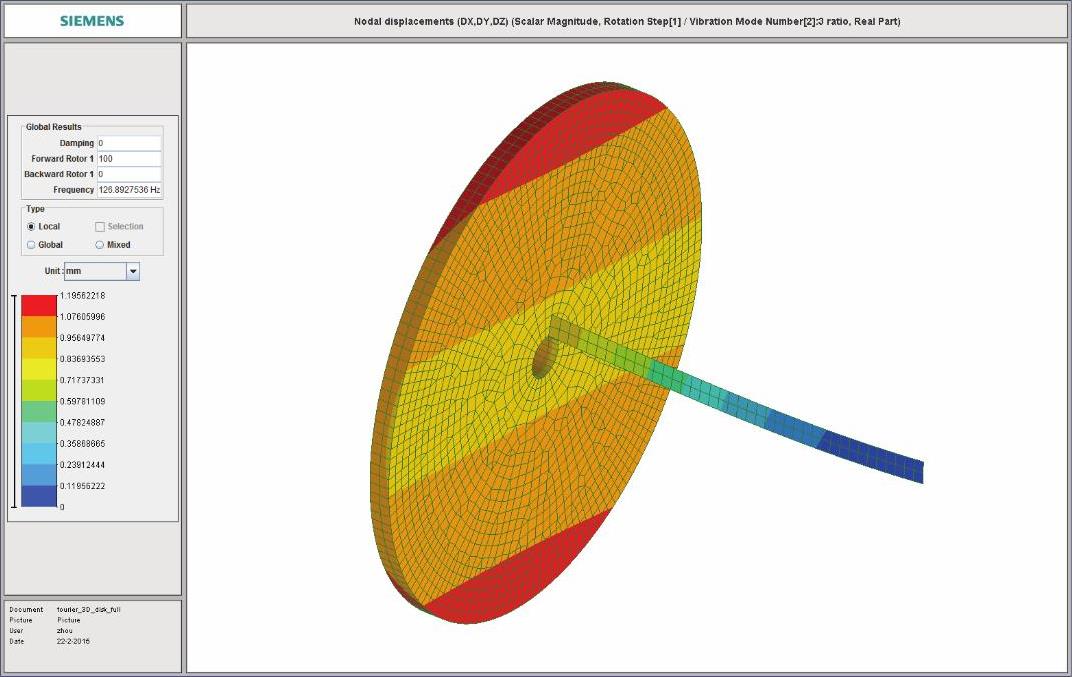
图14-231 第1阶正向涡动临界转速振型
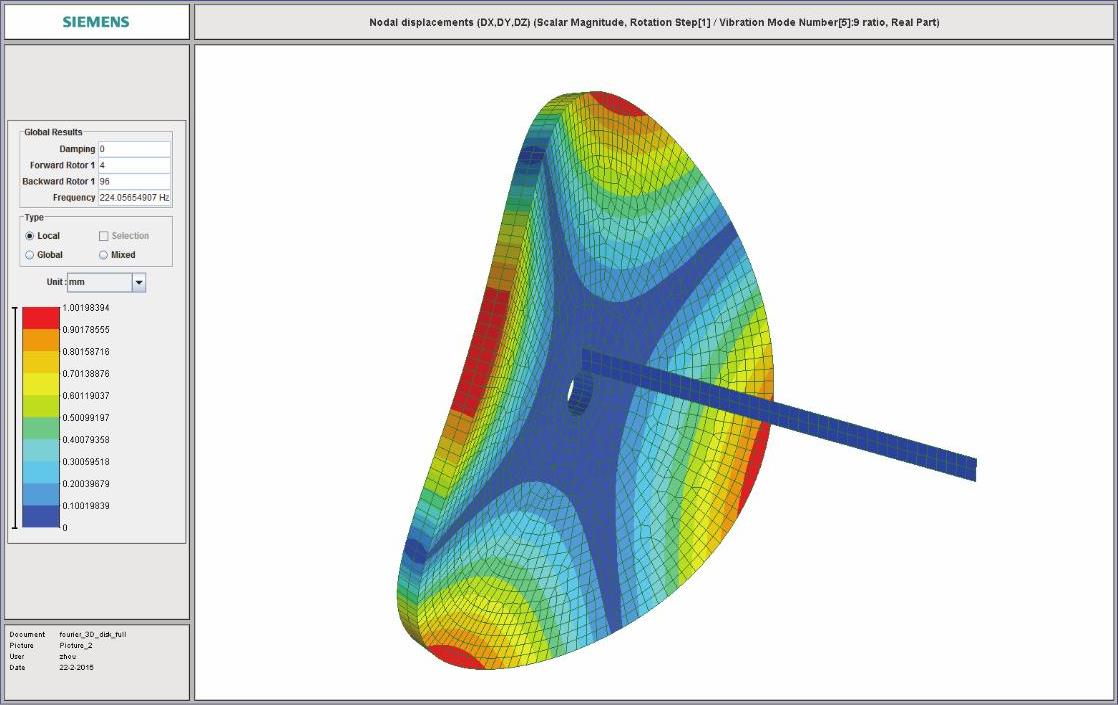
图14-232 耦合振动2节径第1阶振型
为了验证混合模型的精度，下面将其与整体分析模型进行对比。
（15）整体分析模型计算结果振型见图14-235～图14-238，其中第1阶正向涡动临界转速振型见图14-235，耦合振动2节径第1阶振型见图14-236，耦合振动0节径第1阶振型见图14-237，第2阶正向涡动临界转速振型见图14-238。
（16）两种模型的对比情况见表14-18。
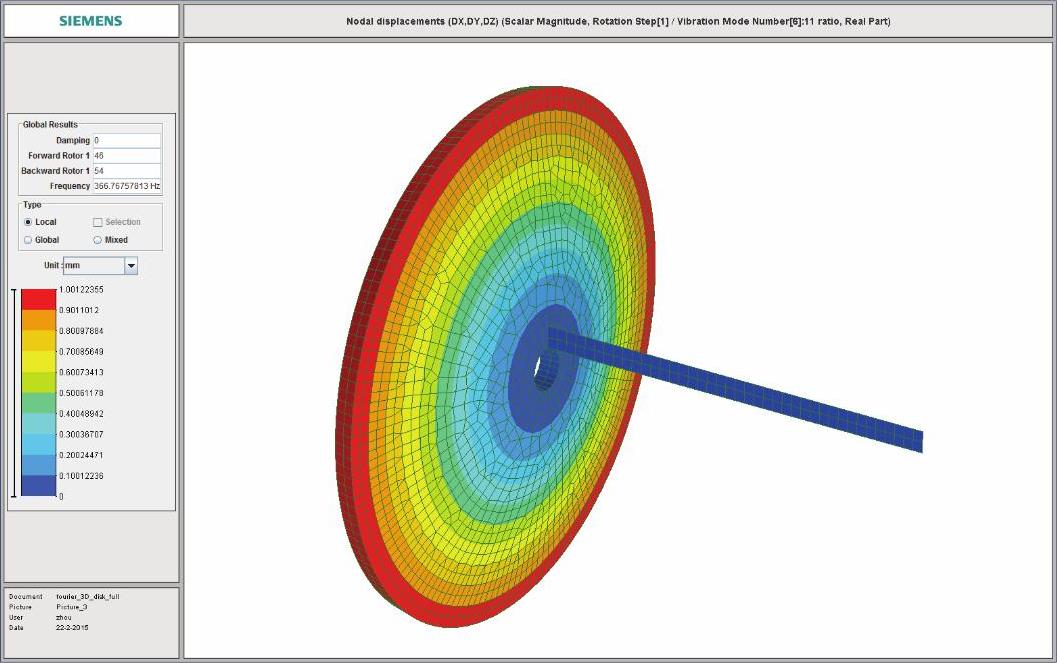
图14-233 耦合振动0节径第1阶振型
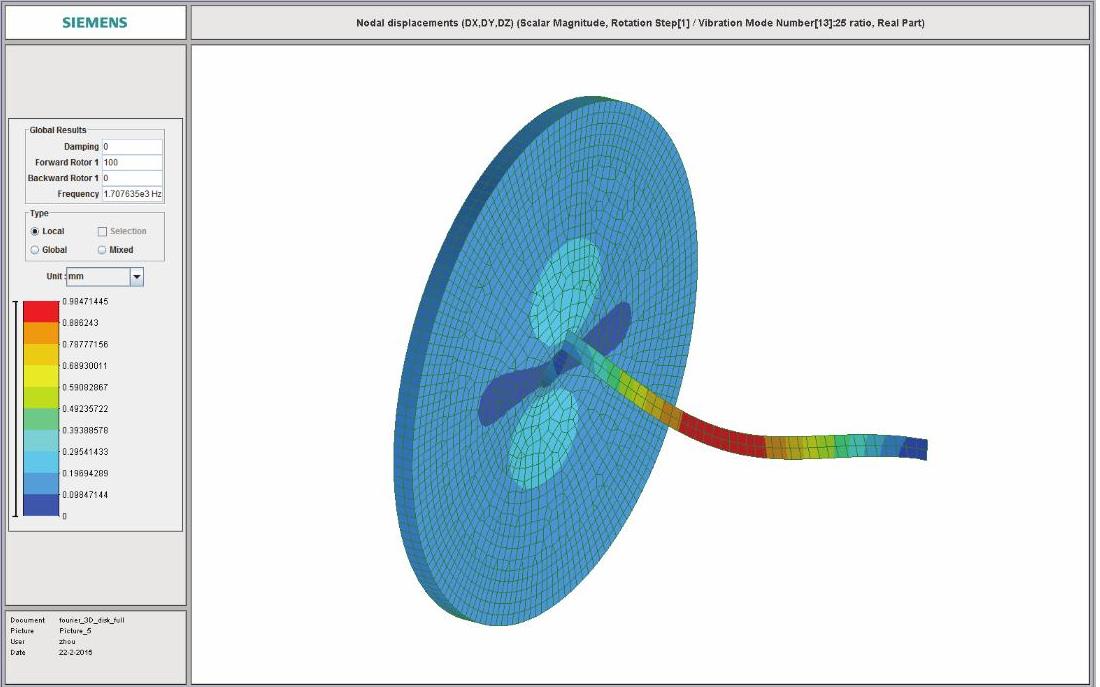
图14-234 第2阶正向涡动临界转速振型
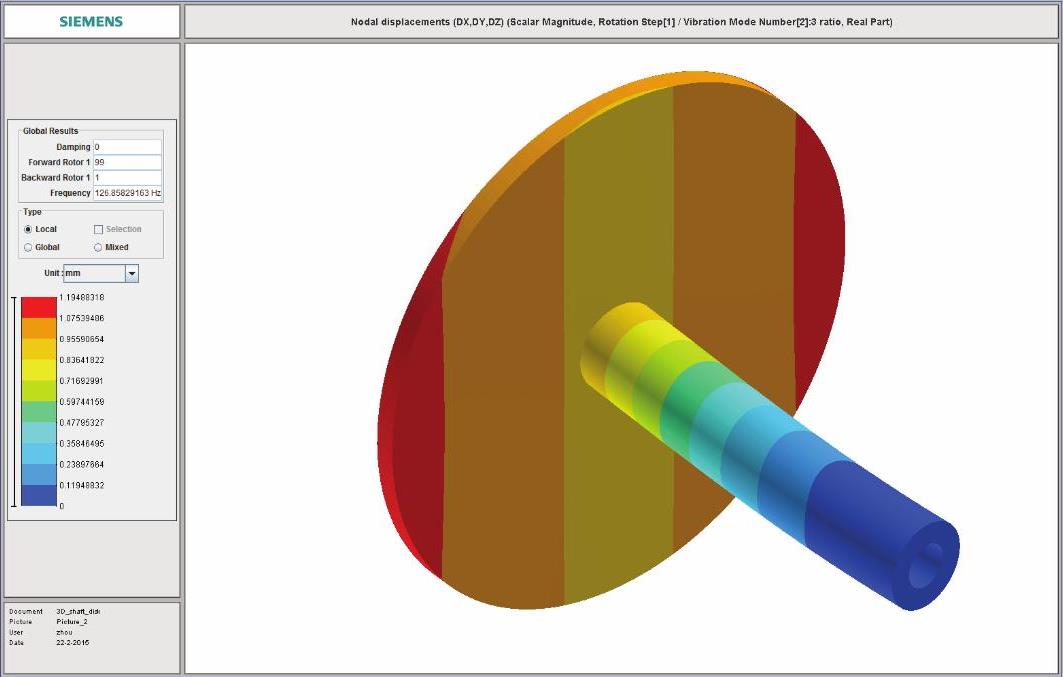
图14-235 第1阶正向涡动临界转速振型
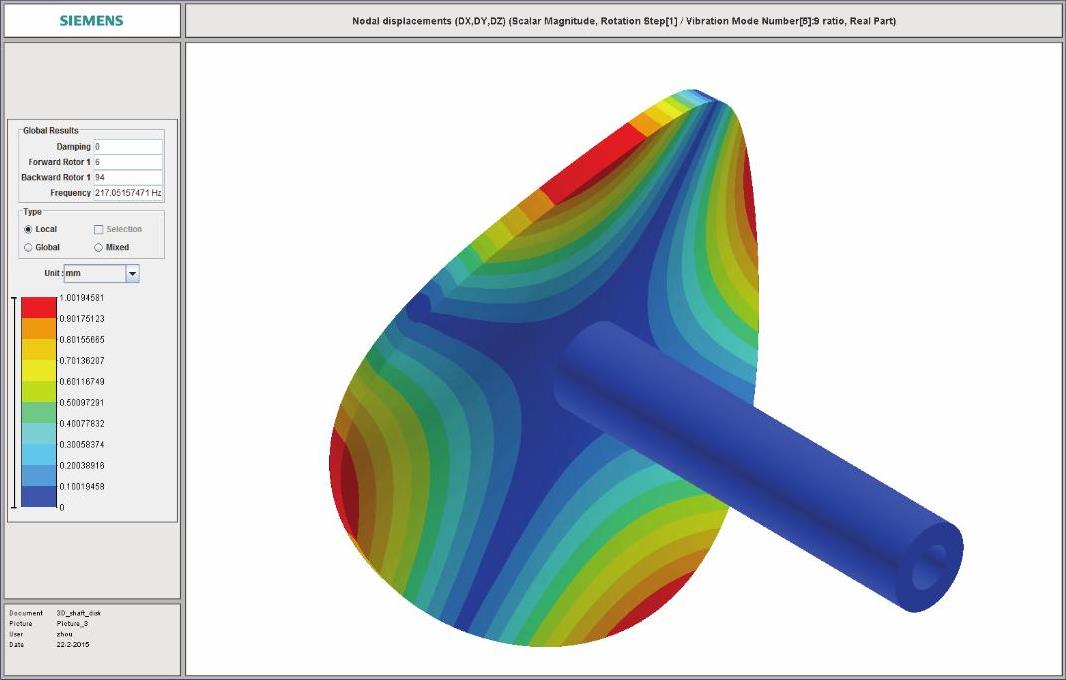
图14-236 耦合振动2节径第1阶振型
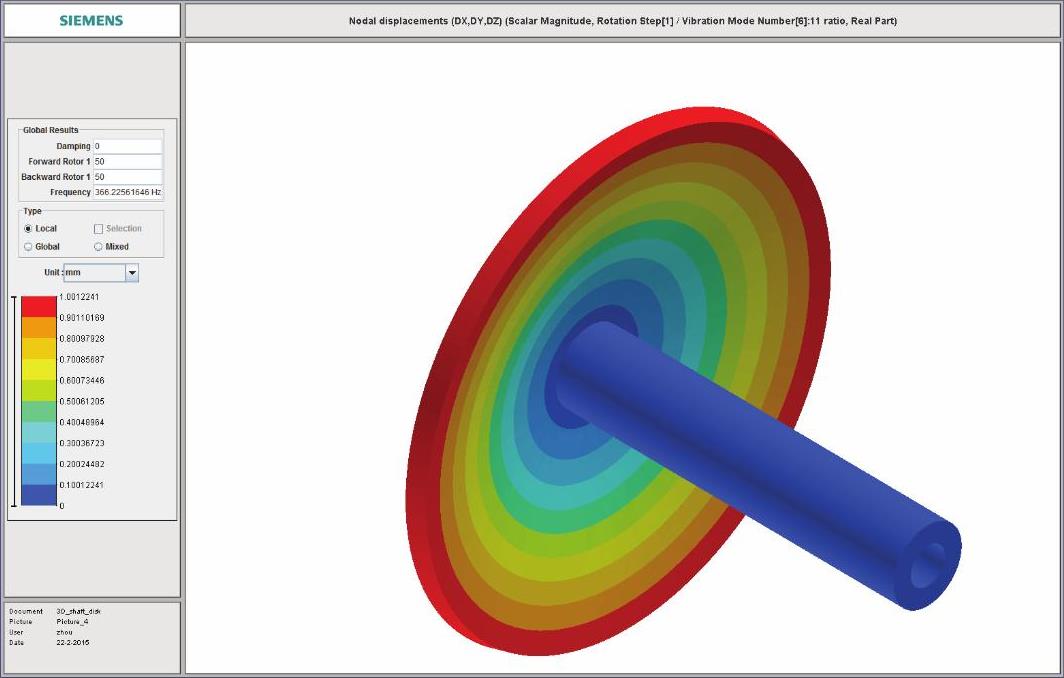
图14-237 耦合振动0节径第1阶振型
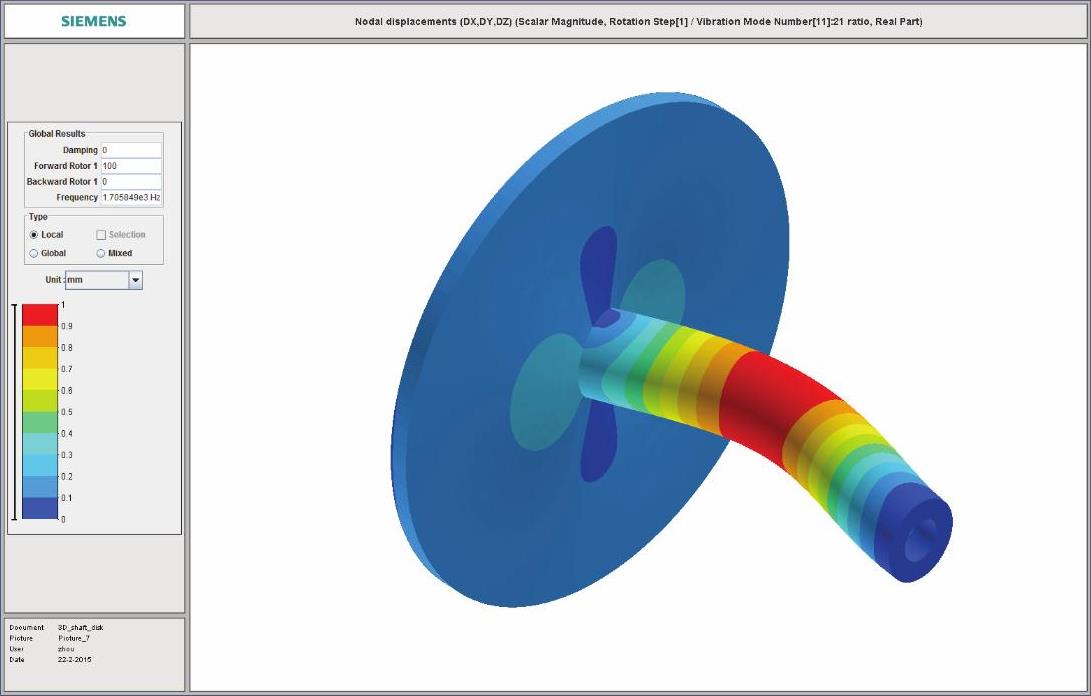
图14-238 第2阶正向涡动临界转速振型
有关SAMCEF有限元分析与应用实例的文章
截止到2015年5月，SAMCEF Field的最新版本是V16.1。SAMCEF Field使用友好的用户环境与SAMCEF系列结构分析工具相结合。SAMCEF Field的功能强大、直观，而且容易使用。如图2-4所示为SAMCEF Field典型的图形界面。SAMCEF Field使用户设计自己的系统只需要一个简单的操作。图2-5 多部件系统级分析模型SAMCEF Field支持众多的求解器，与SAMCEF系列求解器的传递是非常清晰的。SAMCEF Field提示用户定义与应用领域相关的数据，还可以发现不连贯的数据并提示用户更改。......
2023-10-27
本实例使用超单元来建立整个模型。在本书光盘中提供本实例题所有建模、分析和结果确认过程的最终数据库文件和动画文件。图14-131 阶梯轴转子模型表14-16 轮盘的参数在0.1651m和0.287m的位置处分别加两个相同的轴承支撑，轴承支撑的刚度系数和阻尼系数见表14-17。表14-17 轴承支撑的刚度系数和阻尼系数本实例所介绍的各阶段的分析步骤与一般实际工作中的分析过程基本相同。......
2023-10-27
本实例采用梁模型建模对阶梯轴转子进行瞬态响应分析。在本书光盘中提供本实例中所有建模、分析和结果确认过程的最终数据库文件。通过查看算例文件可以对整个分析过程获得一定的了解。表14-9 轮盘的参数表14-10 不平衡质量块的参数注意：在本实例中，需要给定轮盘和不平衡质量块的转速，才能把其不平衡效应考虑进去。表14-11 弹簧支撑的刚度系数和阻尼系数本实例所介绍的各阶段的分析步骤与一般实际工作中的分析过程基本相同。......
2023-10-27
单击Solver模块图标，进入求解模块。在Placed on右侧的下拉列表框中选择VERTEX，在图形画面中选中Point5。Output输出设置如图15-90所示。重复步骤，定义Point11、Point14处的加速度输出。设置求解需要的内存为100。End frequency：扫频终止频率为350 Hz。扫频从180～350Hz，间隔为1Hz，60r/min。Algorithm：谐波响应计算方法为Modal（模态法）。单击图标，提交作业，并显示执行状态的监视对话框。图14-92 监视对话框当计算完成后，单击Close按钮，关闭监视对话框。单击工具条中的保存文件快捷图标进行保存。......
2023-10-27
SAMCEF Machine Tools是机床工具结构分析专业集成软件包。目前，机床领域存在的主要问题如下。解决这些非线性分析问题需要隐式无条件稳定时间积分方法。SAMCEF机床软件包以机构分析和结构分析耦合的数学力学背景为基础。如图2-18所示为SAMCEF Machine Tools创建的典型机床模型。......
2023-10-27
特殊的单元如下。图5-22 给定扭矩的驱动马达例如给一个装配/铰接增加一个驱动马达，步骤如下。选择函数类型并定义。图5-30 线性函数图5-31 阶梯函数图5-32 点对点函数单击图5-29中的按钮，显示函数图象。......
2023-10-27
如图8-6所示，单击Analysis Data模块图标，进入分析数据模块。图8-6 分析数据模块及其快捷命令图标1.设置材料特性在数据树中选择Model。在此菜单中可以选择单元类型，以及是弹性体还是刚性体。在Mass density文本框中输入7.8e3。单击Apply按钮确认输入数据。在Constraint下拉列表框中选择固定约束Clamp。使用鼠标左键拾取右侧圆孔的圆柱面。在Direction选项组中选择Z单选按钮。......
2023-10-27
单击Check图标，如果出现No data incoherence detected，表明数据已经定义完整，不缺少数据。单击Close按钮返回。设置工作目录，浏览并选择目录E：\Work_Sam。设置求解需要的内存为200。Number Of Steps：输入10。Number of Eigen Values：输入特征值数4。单击图标，提交作业，并显示执行状态的监视对话框。当计算完成后，单击Close按钮，关闭监视对话框和Solver Launch对话框。单击工具条中的保存文件快捷图标保存文件。......
2023-10-27
相关推荐