单击Result模块图标，进入结果显示模块。
1．绘制Compbell图
(1)单击Results左侧的
图标，展开的结果数据树如图14-58所示。
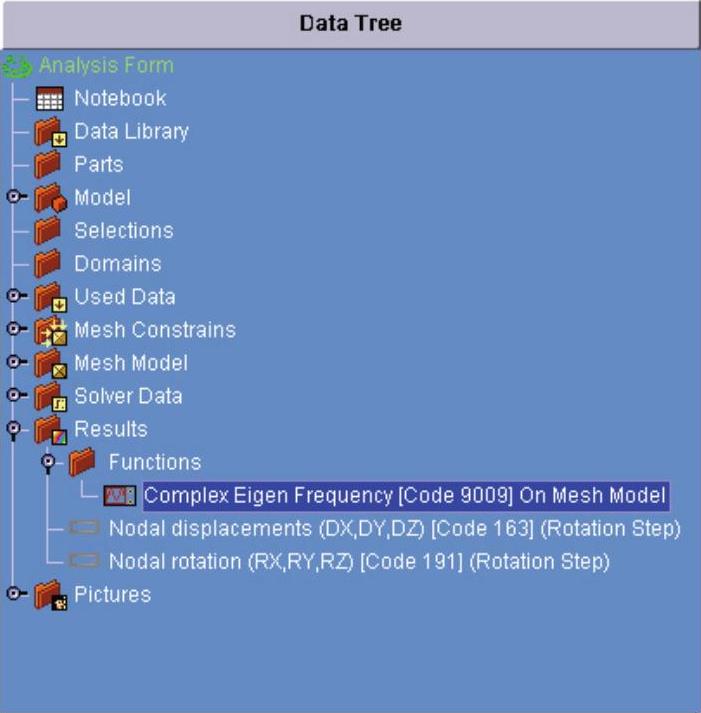
图14-58 结果数据树
（2）双击Functions。
（3）双击Complex Eigen Frequency，得到图14-59所示复频率与转速的关系曲线图。
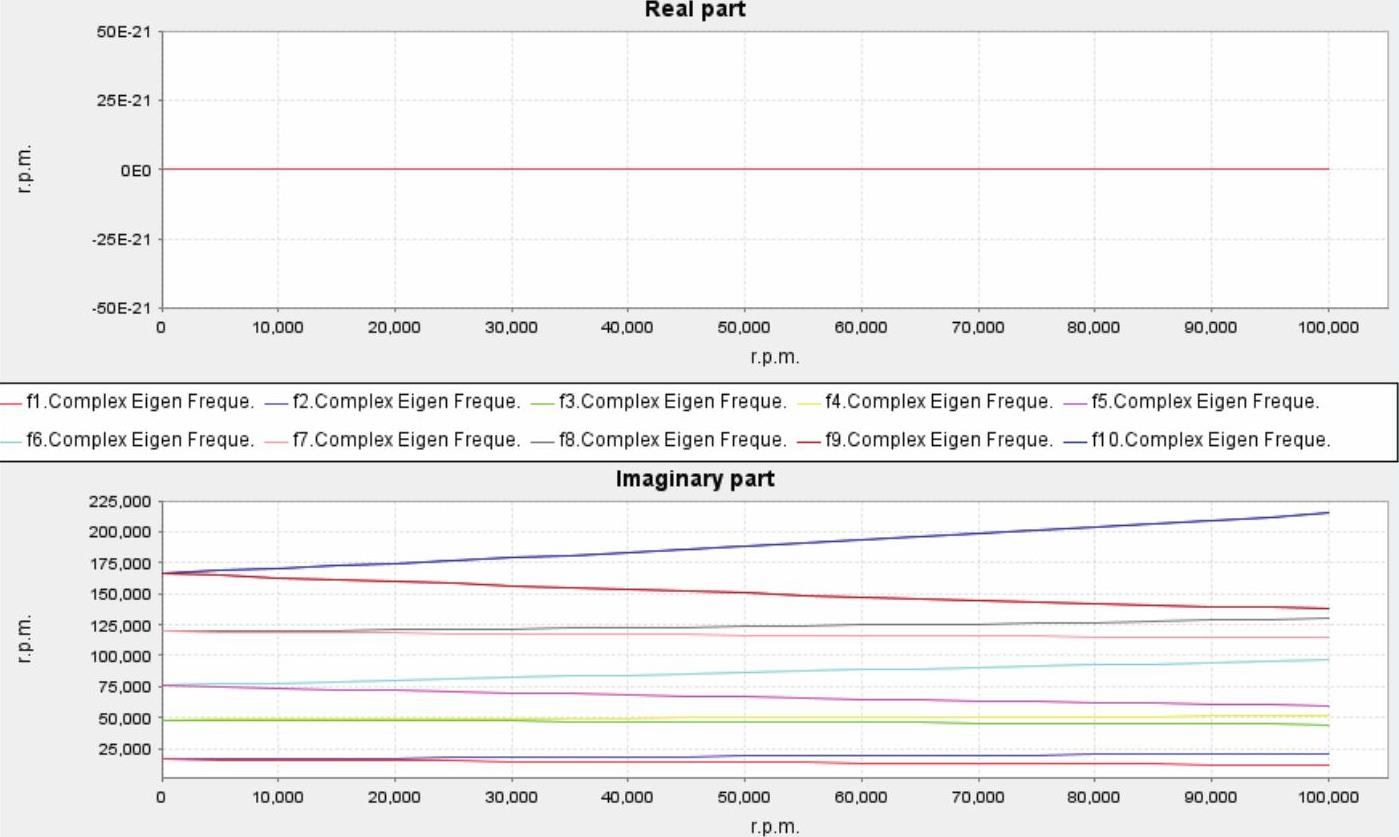
图14-59 复频率与转速的关系曲线图
（4）单击Function Dialog对话框中的
图标，将Complex Option改为Amplitude。
（5）将Ordinate Unit改为tr/s，单位为Hz。
（6）选中Show points复选框以显示数据点。
（7）频率与转速的关系曲线图Compbell图，如图14-60所示。
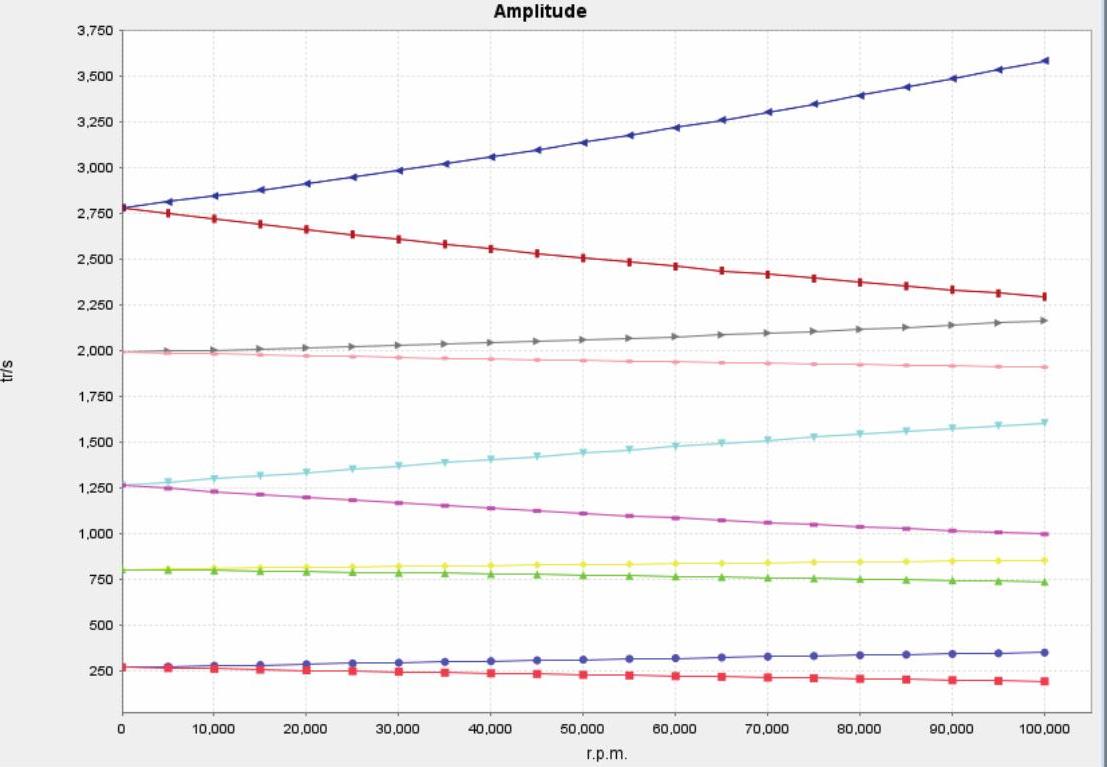
图14-60 Compbell图
2.显示振型图
（1）在数据树中选择Nodal Displacements。
（2）显示第1阶反向涡动频率模态振型图（如图14-61所示）。
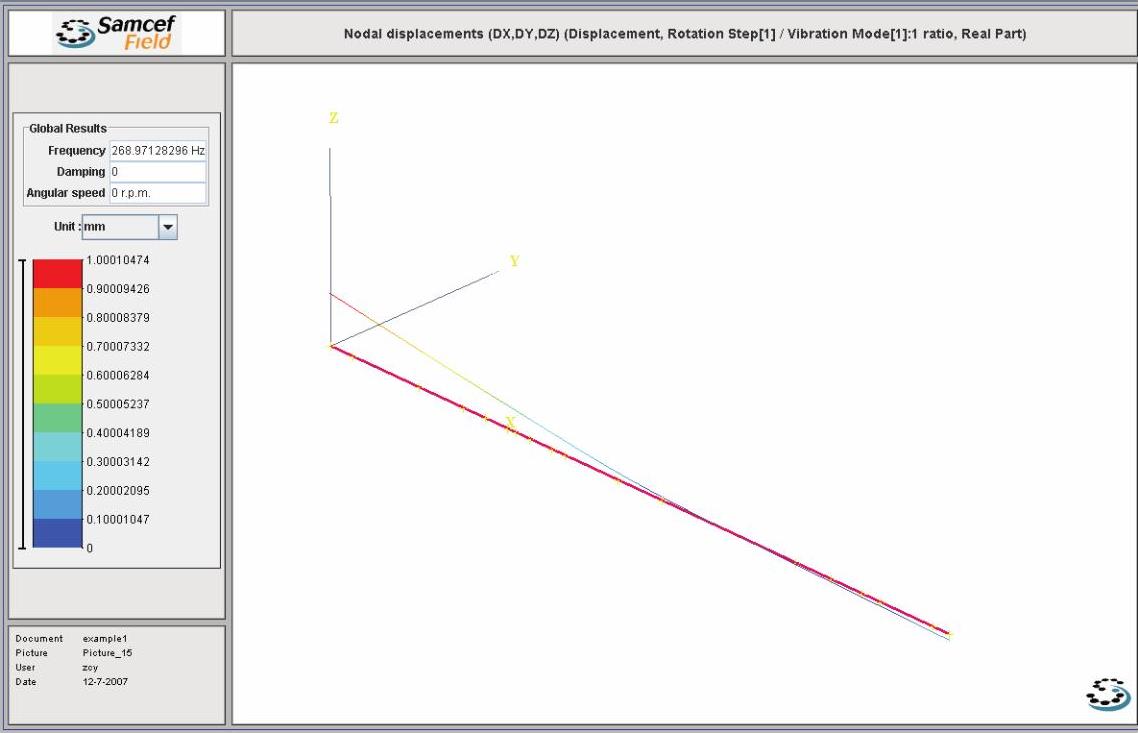
图14-61 第1阶反向涡动频率模态振型图
注意：这里给出的是涡动频率，涡动有正向涡动和反向涡动之分。每个频率都与转速有关，因此在图形左上角处，除了有该阶振型的频率值Frequency为268.97128296 Hz外，还有对应的转速Angular speed为0 r/min。
（3）单击鼠标右键，在弹出的快捷菜单中选择Reference（S）命令，弹出Reference（S）对话框。
（4）如图14-62a所示，Reference（S）对话框中有两个滑块，第一个对应转速步数，即转速，第二个对应频率阶数。用鼠标拖动滑块到频率阶数为2，转速步数为3，即10 000r/min时第1阶正向涡动频率，显示的模态形状如图14-63所示。
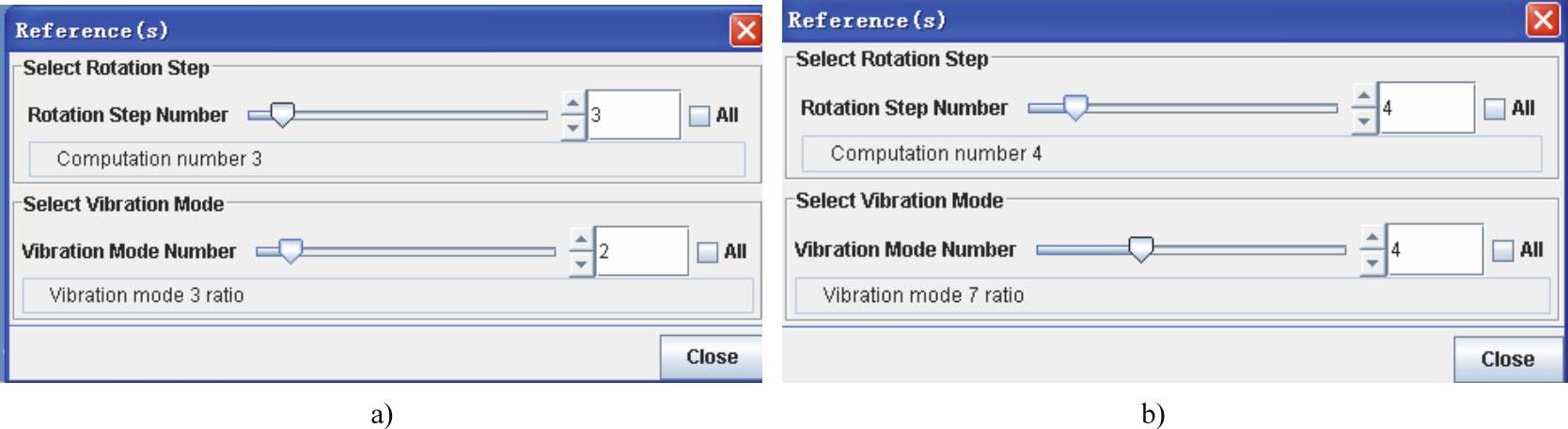
图14-62 Reference（S）对话框
a）步数3模态2 b）步数4模态4
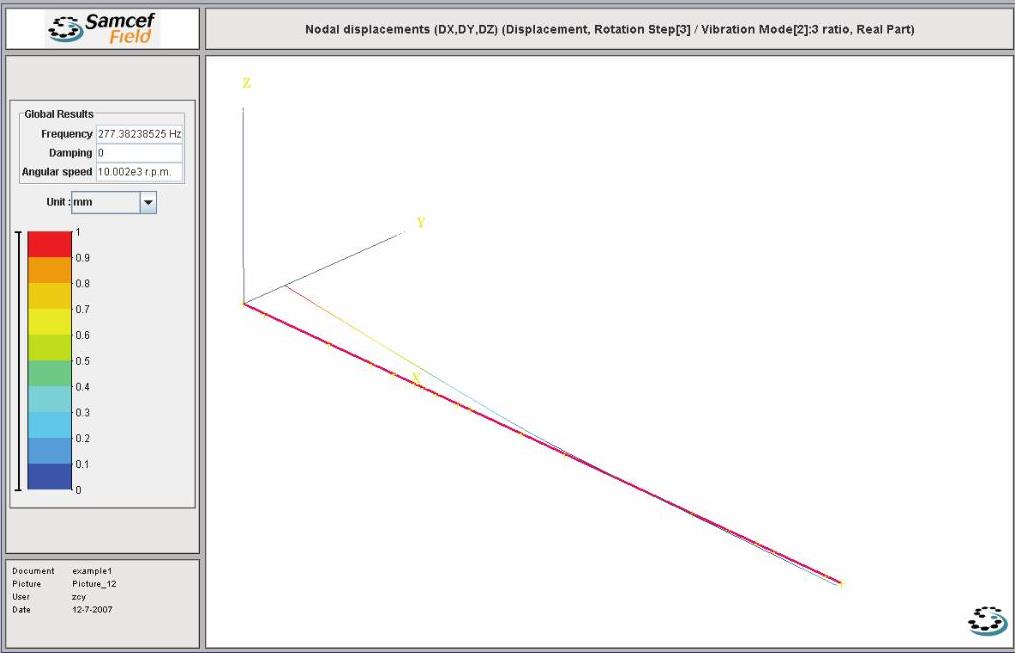
图14-63 Case A的第1阶正向涡动振型图
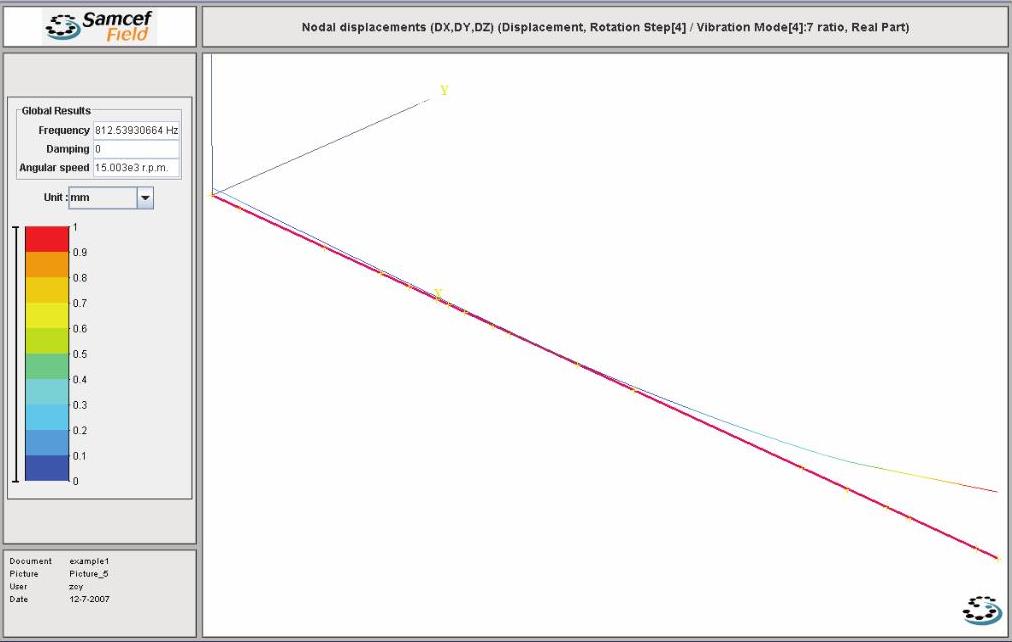
（5）如图14-62b所示，用鼠标拖动滑块到频率阶数4，转速步数为4，即15000r/min时第2阶正向涡动频率，显示的模态形状如图14-64所示。
(www.chuimin.cn)
图14-64 Case A的第2阶正向涡动振型图
（6）单击工具条中的保存文件快捷图标进行保存。
此时计算结果和有限元模型一起保存在SAMCEF Field数据库中。
Case B的复频率与转速的关系曲线图和Compbell图，如图14-65和图14-66所示。
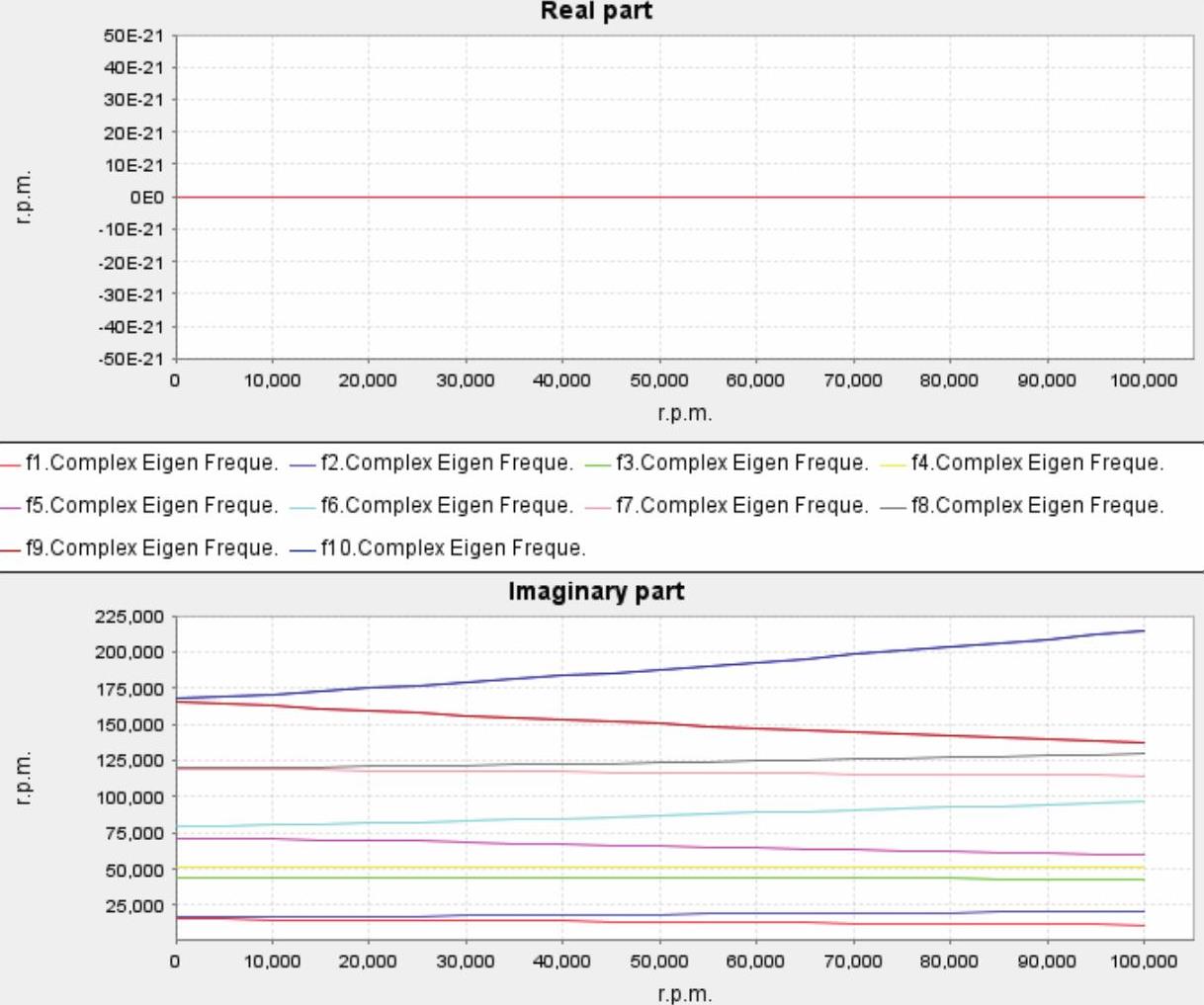
图14-65 Case B的复频率与转速的关系曲线图
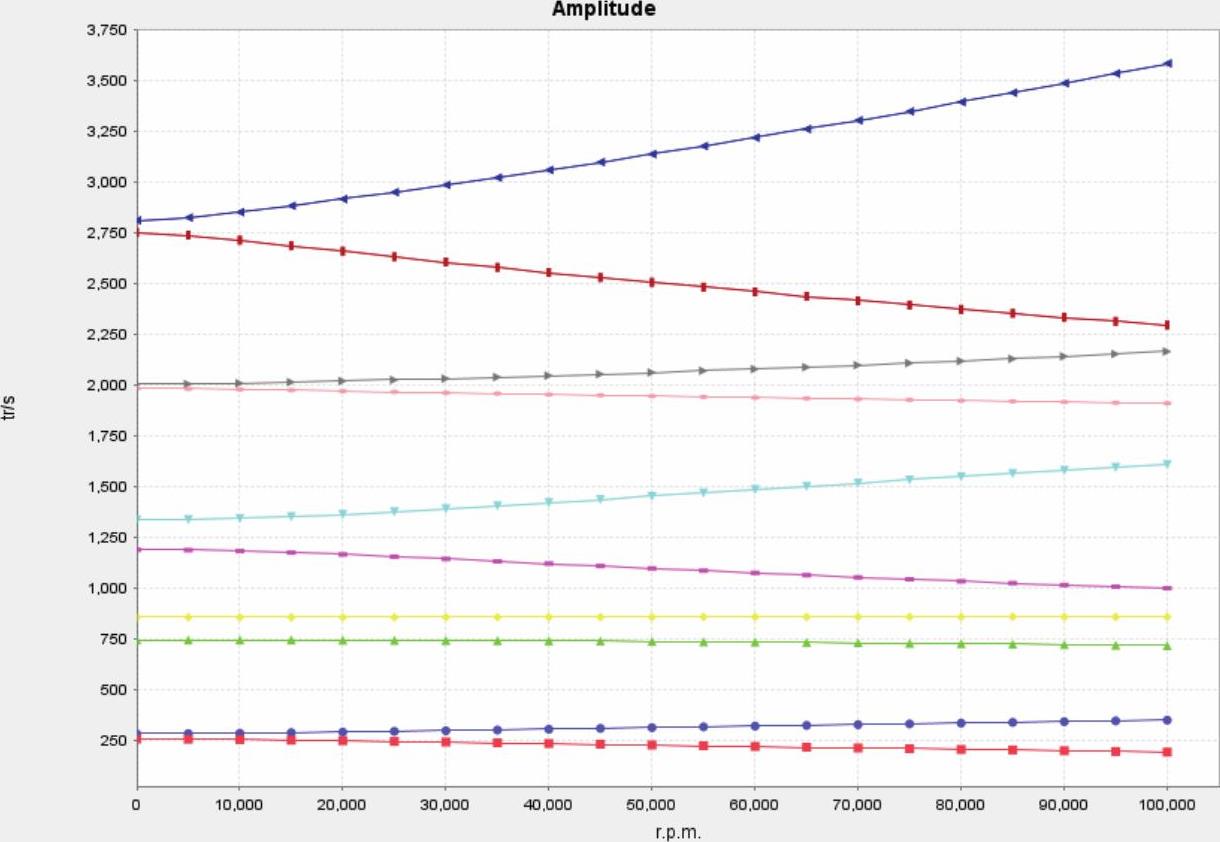
图14-66 Case B的Compbell图
Case B的第1阶反向涡动、第1阶正向涡动和第2阶正向涡动振型图，如图14-67～图14-69所示。
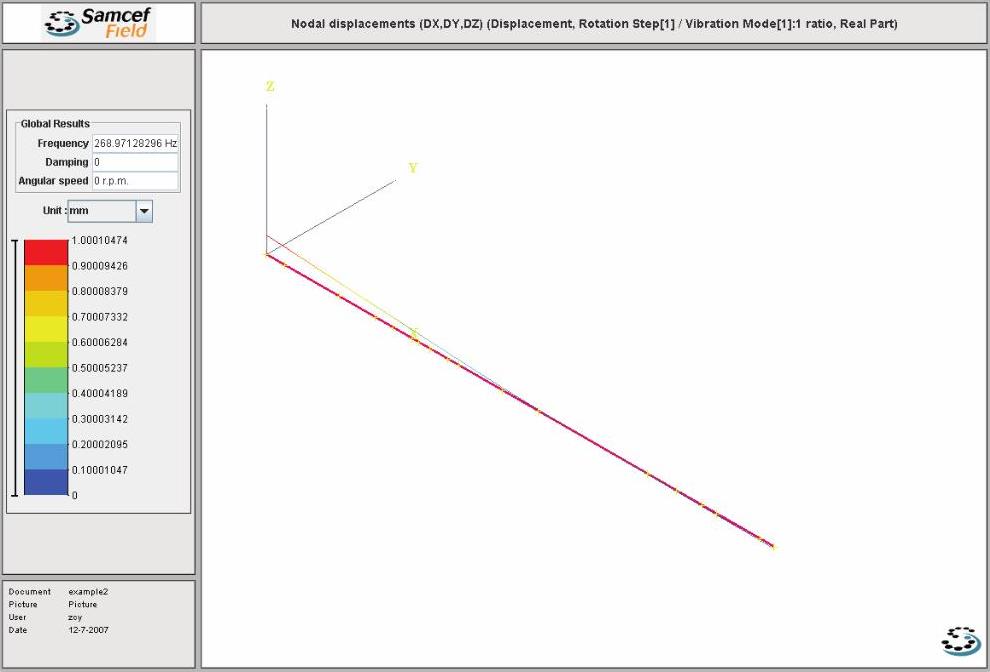
图14-67 Case B的第1阶反向涡动振型图
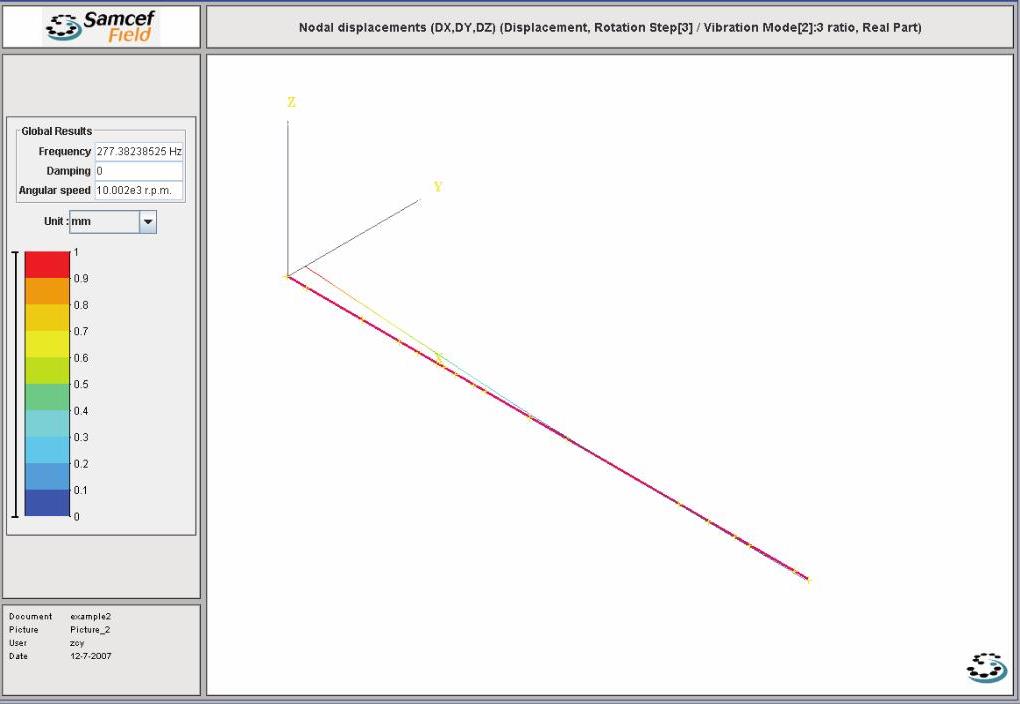
图14-68 Case B的第1阶正向涡动振型图
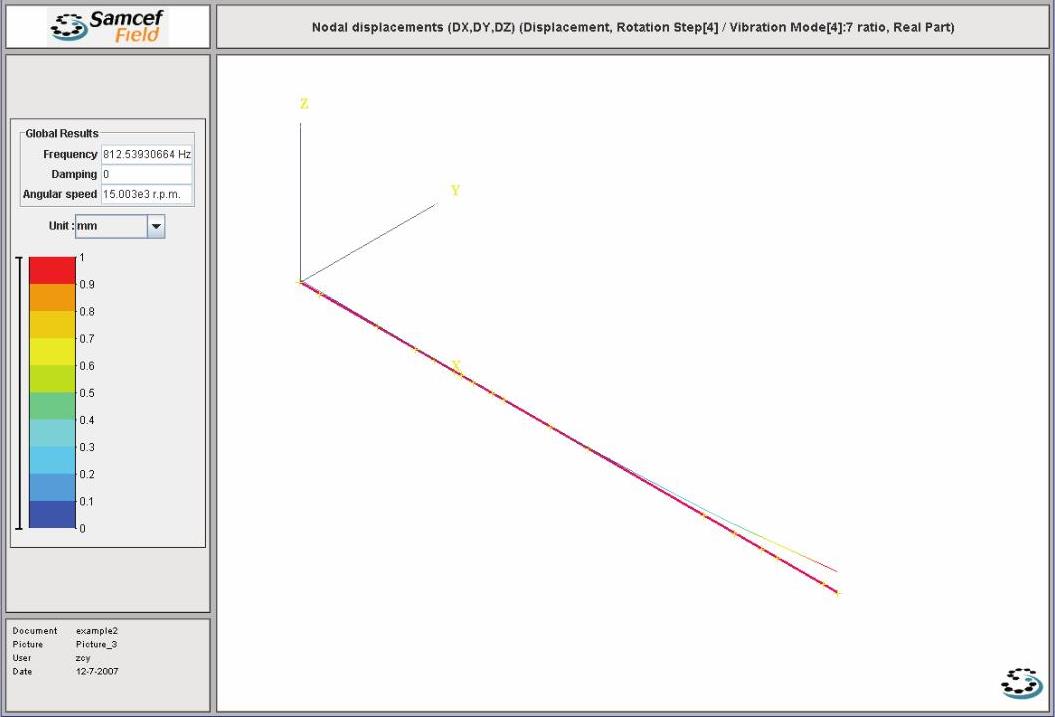
图14-69 Case B的第2阶正向涡动振型图
Case C的复频率与转速的关系曲线图和Compbell图，分别如图14-70和图14-71所示。
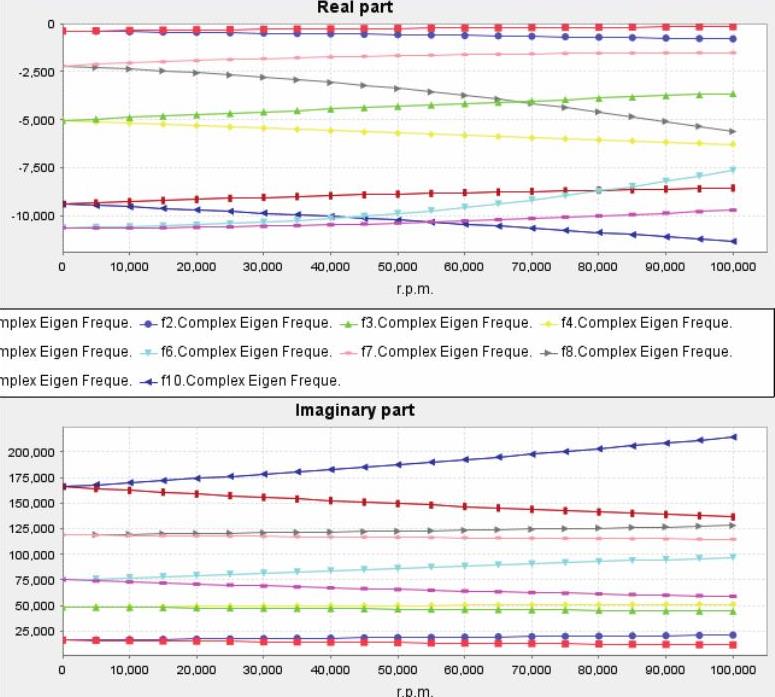
图14-70 Case C的复频率与转速的关系曲线图
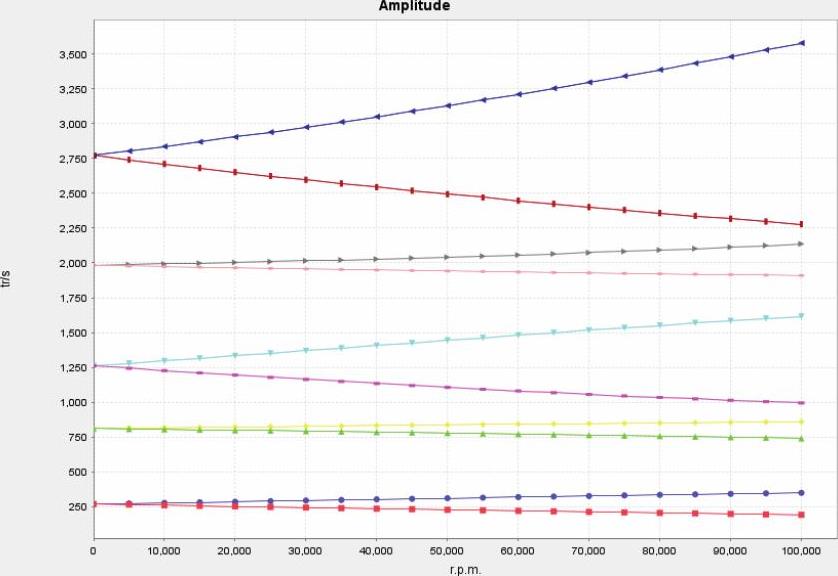
图14-71 Case C的Compbell图
Case C的第1阶反向涡动、第1阶正向涡动和第2阶正向涡动振型图，如图14-72～图14-74所示。
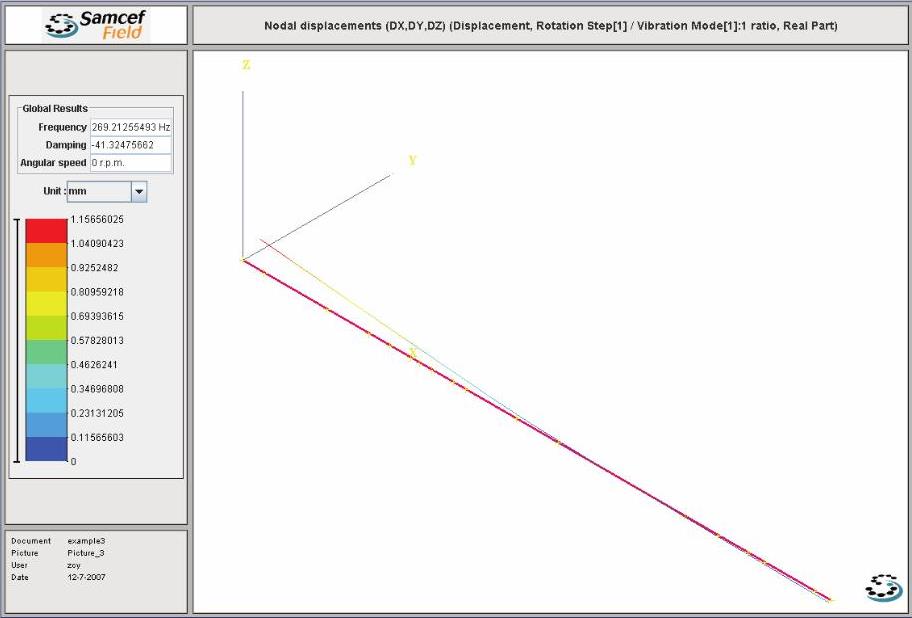
图14-72 Case C的第1阶反向涡动振型图
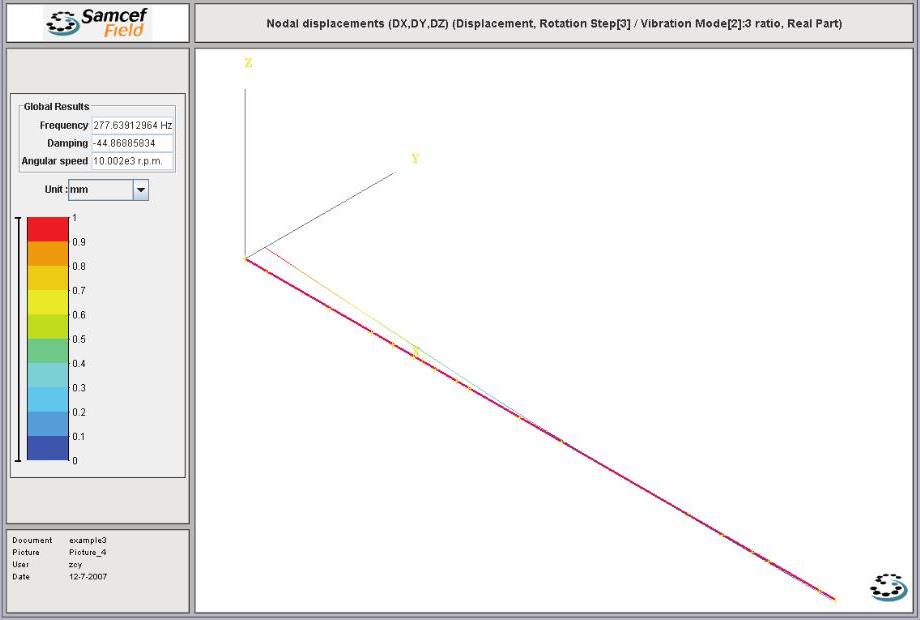
图14-73 Case C的第1阶正向涡动振型图
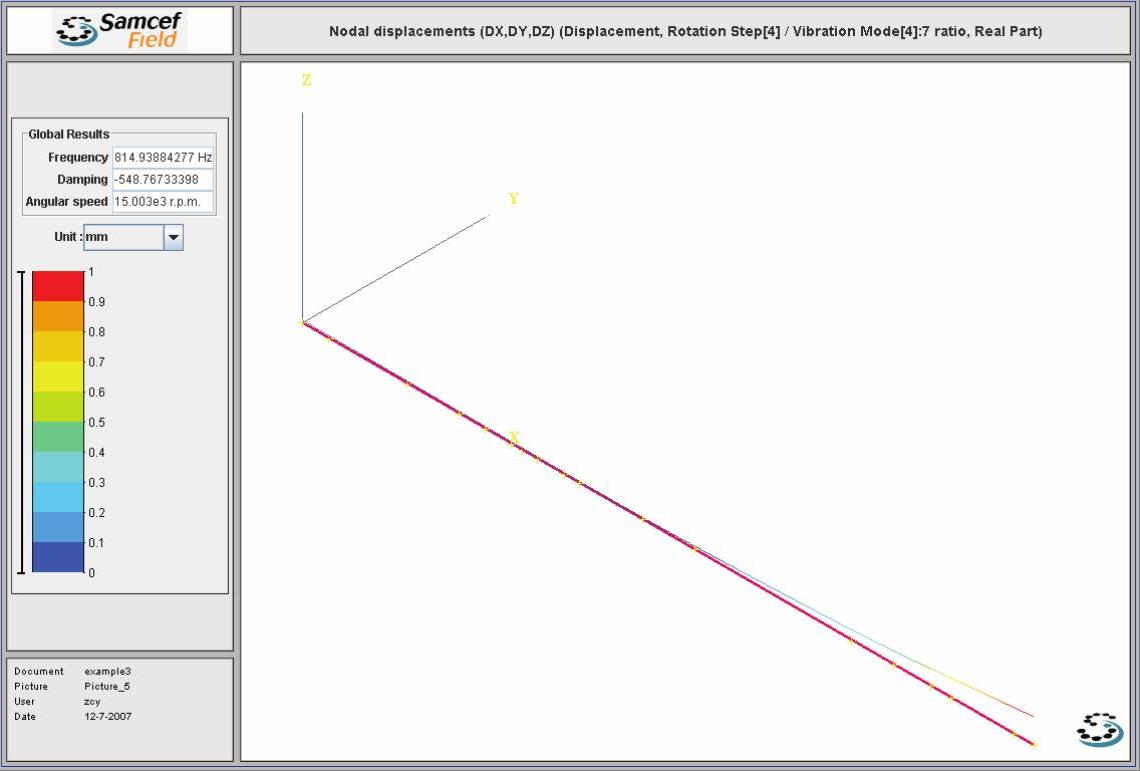
图14-74 Case C的第2阶正向涡动振型图
注意，其阻尼数值分别为Damping-41.32475662、-44.86885834和-548.7673398。
有关SAMCEF有限元分析与应用实例的文章
图14-20 结果显示模块及其快捷命令图标1.绘制Compbell图图14-21所示为结果数据树。图14-23 Compbell图2.显示振型图在数据树中选择Nodal displacements。每个频率都与转速有关，因此在图形左上角处，除了有该阶振型的频率值Frequency 15.4156189Hz，还有对应的转速Angular speed 0 r/min。用鼠标拖动滑块到频率阶数为2，转速步数为3，即1200r/min时，第1阶正向涡动频率显示的模态形状如图14-26所示。图14-27 第2阶正向涡动频率模态振型图单击工具条中的保存文件快捷图标进行保存。......
2023-10-27
单击Result模块图标，进入结果显示模块。双击Acceleration：Acceleration_on_1_vertex_of_Wire1 Comp2[C9183]Node 10，即为Point5在Y方向的加速度响应。单击鼠标右键，在弹出的快捷菜单中选择Reference命令，弹出Reference对话框，如图14-113所示。图14-112 位移与时间的关系曲线图图14-113 Reference对话框将滑块调到173，对应时间为1.72s。转子系统在1.72s时的位移响应图如图14-114所示，可得最大位移为13.22mm。图14-114 1.72s时的位移响应图......
2023-10-27
单击Result模块图标，进入结果显示模块。此结果跟13.2节的实例求解的第1阶临界转速值基本对应。单击鼠标右键，在弹出的快捷菜单中选择Reference命令，弹出Reference对话框。图14-95 设置频率为250Hz的Reference对话框图14-96 第一峰值位移响应图如图14-97所示，将Reference对话框中的滑块调到113，即对应频率292Hz。位移达到第二个峰值时的响应图如图14-98所示，最大位移10.950328mm。......
2023-10-27
图8-46 结果显示模块及其快捷命令图标单击数据树中Results左侧的图标，展开结果数据树。选择等效应力Equivalent stress，显示图8-47所示的叶轮应力云图。选择等效应力Equivalent stress，单击鼠标右键，弹出图8-49所示快捷菜单并选择Mesh on Result命令。在图形工具条中执行旋转视图命令，调整叶轮视图角度后的应力云图。单击OK按钮，生成一个名称为Picture的图片文件并存放到数据树Pictures下。图8-54 准则菜单图8-55 选择准则单击Apply按钮，生成图8-56所示位移云图。......
2023-10-27
截止到2015年5月，SAMCEF Field的最新版本是V16.1。SAMCEF Field使用友好的用户环境与SAMCEF系列结构分析工具相结合。SAMCEF Field的功能强大、直观，而且容易使用。如图2-4所示为SAMCEF Field典型的图形界面。SAMCEF Field使用户设计自己的系统只需要一个简单的操作。图2-5 多部件系统级分析模型SAMCEF Field支持众多的求解器，与SAMCEF系列求解器的传递是非常清晰的。SAMCEF Field提示用户定义与应用领域相关的数据，还可以发现不连贯的数据并提示用户更改。......
2023-10-27
单击Solver模块图标，进入求解模块。在Placed on右侧的下拉列表框中选择VERTEX，在图形画面中选中Point5。Output输出设置如图15-90所示。重复步骤，定义Point11、Point14处的加速度输出。设置求解需要的内存为100。End frequency：扫频终止频率为350 Hz。扫频从180～350Hz，间隔为1Hz，60r/min。Algorithm：谐波响应计算方法为Modal（模态法）。单击图标，提交作业，并显示执行状态的监视对话框。图14-92 监视对话框当计算完成后，单击Close按钮，关闭监视对话框。单击工具条中的保存文件快捷图标进行保存。......
2023-10-27
在数据树中双击Results，再次双击Functions，展开图14-283所示结果列表。图14-283 Functions选项列表双击相对位移结果列表Relative Displacement：Ground_Rolling-element_Bearing_on_1_vertex_of_Wire1 Comp1[C9530]Element 92和Comp1[C9530]Element 92，显示图14-284所示图形，这是位于位置0mm处轴承的时域相对位移曲线。图14-285 轴承频率响应相对位移曲线（幅值）单击图标，单击f1和f2右侧的Displayed Fuction按钮，关闭f1和f2，只保留f3，单击OK按钮，轴承相对位移响应曲线如图14-286所示。......
2023-10-27
本实例使用超单元来建立整个模型。在本书光盘中提供本实例题所有建模、分析和结果确认过程的最终数据库文件和动画文件。图14-131 阶梯轴转子模型表14-16 轮盘的参数在0.1651m和0.287m的位置处分别加两个相同的轴承支撑，轴承支撑的刚度系数和阻尼系数见表14-17。表14-17 轴承支撑的刚度系数和阻尼系数本实例所介绍的各阶段的分析步骤与一般实际工作中的分析过程基本相同。......
2023-10-27
相关推荐