SAMCEF Rotor是针对转子动力学的专业解决方案，它善于解决转子的动力学问题，例如转子的涡动频率、临界转速、瞬态分析和谐波响应分析等。这种十分灵活而又强大的转子混合建模技术也是SAMCEF Rotor软件独有的。在SAMCEF Rotor软件中可以把基础结构和转子系统统一起来研究其振动特性。另外，在SAMCEF Rotor软件中也可以把柔性静子做成超单元集成到整个系统模型中。......
2023-10-27
超单元在SAMCEFRotor软件中的应用实例
【摘要】：SAMCEF Rotor软件中使用的简化模型主要是指超单元，超单元通过简化的刚度、质量、阻尼矩阵和载荷向量描述了子结构。注意GUYAN方法对线性静力问题是准确的，在动力学分析中，和CRAIG与BAMPTON方法一样，它是近似的，并且可以通过使用附加模态来改良。例如，图13-7显示一个外套被分成了四个部分，每一个定子的组分通过超单元来描述。
SAMCEF Rotor软件中使用的简化模型主要是指超单元，超单元通过简化的刚度、质量、阻尼矩阵和载荷向量描述了子结构。如果子结构是转子的一部分，那么就会产生回转和循环力矩阵。
产生这些简化矩阵有很多方法，当前最常用的是GUYAN方法和CRAIG与BAMPTON方法简化方法。第一种方法是第二种方法的特殊情况，CRAIG与BAMPTON方法是部件模态综合方法的一部分，作为模态的两种，组合模态方法被用来产生简化模型。
注意GUYAN方法对线性静力问题是准确的，在动力学分析中，和CRAIG与BAMPTON方法一样，它是近似的，并且可以通过使用附加模态来改良。
当部件模态方法在动力学分析中使用时，每一个子结构的行为都通过两种类型的部件模态的联合来表述：约束模态（静力变形）和子结构的正则振动模态（独动态变形）。这些部件模态由自由子结构的无阻尼动力学方程决定，自由度的分类是通过几个子结构共享的边界自由度，或者是仅考虑子结构的内部自由度来划分的。强迫模态由赋值、每一个边界自由度的单元位移和其他固定的边界自由度来决定。正则模态对应的自由模态是通过固定子结构边界来获得的。
缩减的模型于是描述成两组自由度：边界自由度和内部自由度。物理自由度主要定位于子结构的边界和内部保留模态，下面的关系描述了原始模型和缩减模型的自由度关系：
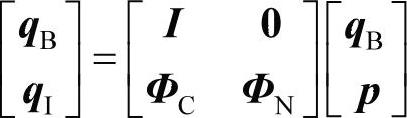(www.chuimin.cn)
其中，qB是边界自由度的向量；qI是内部自由度的向量；ΦC是约束静力模态矩阵；ΦN是正则模态矩阵；p是保留正则模态向量。
当简化的关系适用于势能和动能时，简化的刚度和质量矩阵也就得到了。如果子结构是转子，简化的回转矩阵也用同样的方式建立。
例如，图13-7显示一个外套被分成了四个部分，每一个定子的组分通过超单元来描述。
图13-7 超单元模型
有关SAMCEF有限元分析与应用实例的文章
- 详细阅读
-
SAMCEF有限元分析与应用实例中的单元参数详细阅读
和体单元一样，用户可以在局部坐标系下定义质量和转动惯量特性。图5-39 定义复合材料层图5-40 复合材料体定义显示标志5.膜单元图5-41所示为膜单元定义对话框。图5-45 刚性梁单元定义对话框8.杆单元对于杆只需定义截面面积，如果是刚性的，可以定义杆的质量。图5-49 傅里叶壳单元定义对话框......
2023-10-27
-
VERITAS备份软件在高校图书馆中的应用详细阅读
VERITAS备份软件在人大图书馆中的应用李伶 储继华摘要：备份是图书馆进行数据保护的常用手段。在人大图书馆众多的应用系统中，很多系统是由资源加工、处理与对外发布、服务模块组成，并且几项功能共同安装于一台服务器上。具体备份策略如下：4．VERITAS在人大图书馆数据备份中的应用4．1 VERITAS NetBackup整合了不同平台的备份管理通过备份服务器上的Veritas NetBackup软件，在同一管理窗口使用一个应用程序就能管理不同平台的所有介质，实现数据......
2023-11-30
-
Office办公软件中的单元格引用及用法详细阅读
单元格引用是Excel中的术语，指用单元格在表中的坐标位置来标识，以指明公式中所使用的数据的位置。还可以引用同一个工作簿不同工作表的单元格或区域、不同工作簿的单元格或区域，甚至其他应用程序中的数据。相对引用分以下几种情况：①“单元格相对引用”：用单元格所在的列标和行号作为其引用。例如，E6引用了第E列与第6行交叉处的单元格。......
2023-11-23
-
LDRAtestbed在火箭炮软件静态测试中详细阅读
为了进一步掌握某型火箭炮软件产品的质量状况，通过静态测试尽早发现软件中存在的缺陷，对软件产品进行完善和修订达到提升软件产品质量的目的。以某火箭炮软件代码静态测试的实际应用，证明这种方法的实施能够达到提升软件产品质量的效果。......
2023-06-23
-
光滑铰链约束在工程应用中的形式与实例详细阅读
工程中光滑铰链约束应用广泛，形式多样，常见的主要有以下三种类型：固定铰链支座约束、可动铰链支座约束、中间铰链约束。约束反力的作用线不能预先定出，但约束反力垂直于轴线并通过铰链中心。实例：在桥梁、屋架等结构中经常采用可动铰链支座约束，如图2-22 所示。若相连接的两个构件均不固定，则称为中间铰链。......
2023-06-19
-
特殊单元示例及应用-SAMCEF有限元分析与详细阅读
特殊的单元如下。图5-22 给定扭矩的驱动马达例如给一个装配/铰接增加一个驱动马达，步骤如下。选择函数类型并定义。图5-30 线性函数图5-31 阶梯函数图5-32 点对点函数单击图5-29中的按钮，显示函数图象。......
2023-10-27
-
Excel软件在光偏振实验数据处理中的应用详细阅读
Excel软件在光偏振实验数据处理中的应用武汉东湖学院基础课部物理教研室徐进霞，刘雅娴本文介绍了Excel在光偏振实验数据处理中的应用步骤。图7I-θ的曲线四、结论本文分步骤介绍了Excel在光偏振实验数据处理中的应用。用Excel来进行光偏振实验数据处理不仅可以实现数据处理简单化，还可以准确作图；对提高学生计算机应用能力、开拓视野、激发学生的创造能力，以及对今后的学习和工作都有大有裨益。......
2023-12-04
相关推荐