【摘要】:图13-1为一个典型的汽轮机转子梁-弹簧-集中质量模型。图13-1 梁-弹簧-集中质量模型二维傅里叶级数模型:转子采用二维傅里叶多谐波单元模拟。图13-2 二维傅里叶级数转子模型为了促进轴对称转子模型和与它耦合的固定部件或其他旋转部件的使用,也为了要考虑陀螺效应和阻尼的影响,已经更新了多谐波实体单元和壳单元库。图13-5 三维转子模型当需要加速计算时,就会想到简化转子模型,这可以通过超单元实现。
SAMCEF Rotor软件有三种有限元模型可用来描述转子系统。
一维(1D)模型:转子系统用梁、弹簧和集中质量单元来模拟。这个模型计算速度快,它适用于有大量参数需要调整时的初期设计分析。但是,比如前文提到的飞机发动机,这个模型的细节可能需要许多专业的经验,还可能消耗很多时间。图13-1为一个典型的汽轮机转子梁-弹簧-集中质量模型(软件中可以显示实际的截面形状)。

图13-1 梁-弹簧-集中质量模型
二维(2D)傅里叶级数模型:转子采用二维傅里叶多谐波单元模拟。对于转子动力学方面的应用,为了描述轴向变形、扭矩变形和弯曲变形与陀螺力矩耦合,必须考虑0和1节径的谐波。这种模型适合创建旋转设备更精细的计算分析模型,它非常适合于带有多数目叶片的旋转机械的建模,也适合圆锥转子的建模。图13-2为一个典型的燃气轮机二维模型。
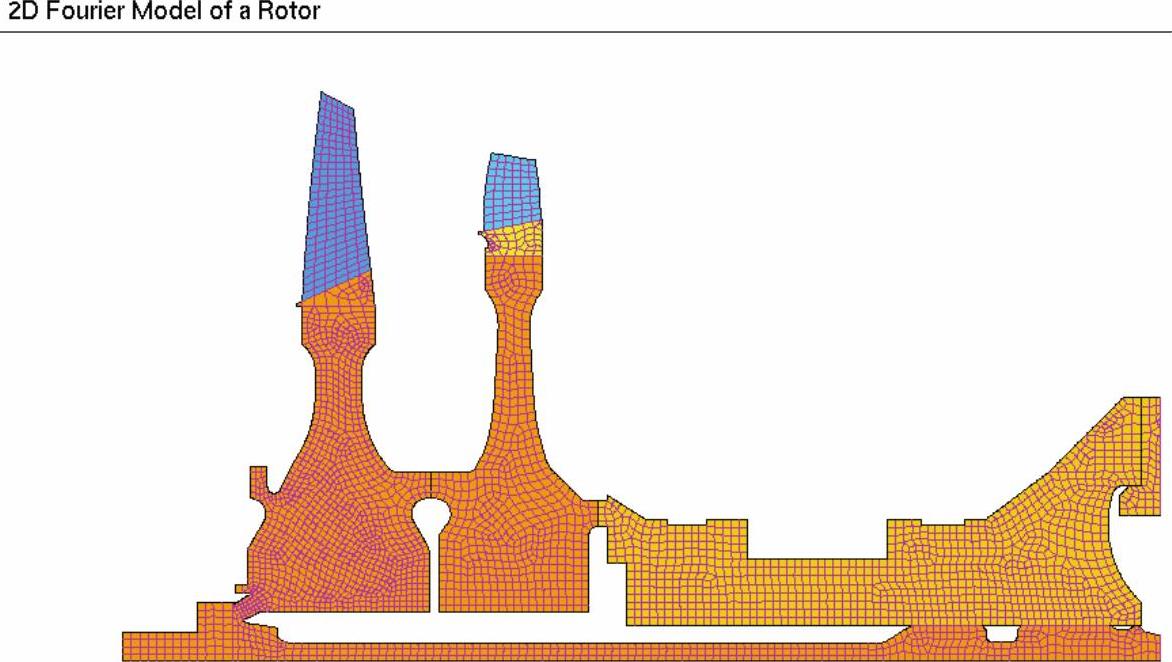
图13-2 二维傅里叶级数转子模型
为了促进轴对称转子模型和与它耦合的固定部件或其他旋转部件的使用,也为了要考虑陀螺效应和阻尼的影响,已经更新了多谐波实体单元和壳单元库(见图13-3)。
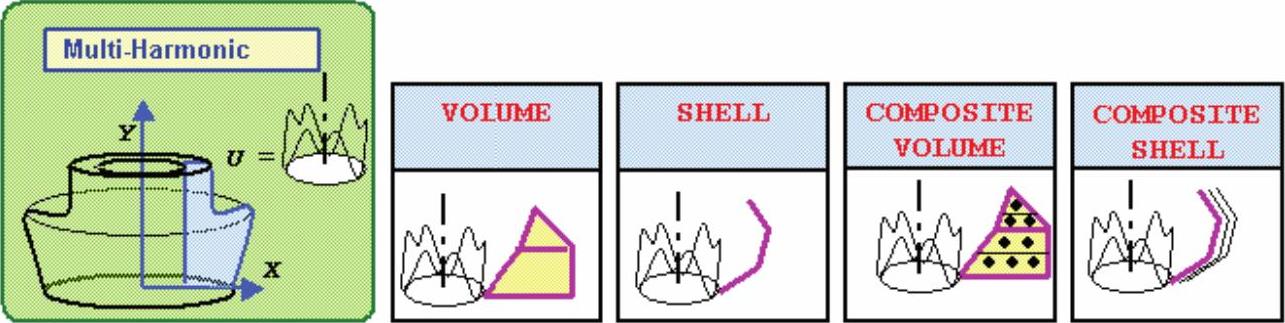
图13-3 多次谐波单元
为了考虑转子的离心刚度,同时采用不同谐波是一个简单的方法,在瞬态分析中,它可以在同样的运行中做到。另一方面,单元库包含一种专门的连接单元,这种单元可以考虑三维(3D)模型和傅里叶模型之间或轴上的一个三维节点和傅里叶模型之间的耦合,如图13-4所示。
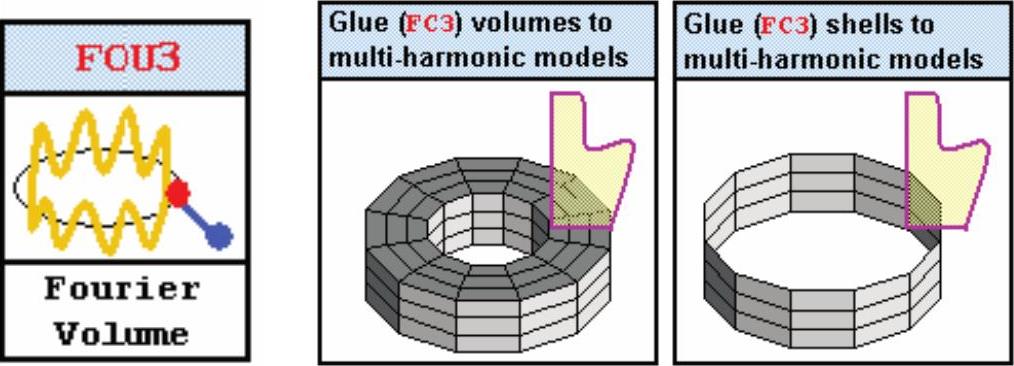
图13-4 连接单元
位移场采用傅里叶级数形式展开,有限元建模在参考面上进行。
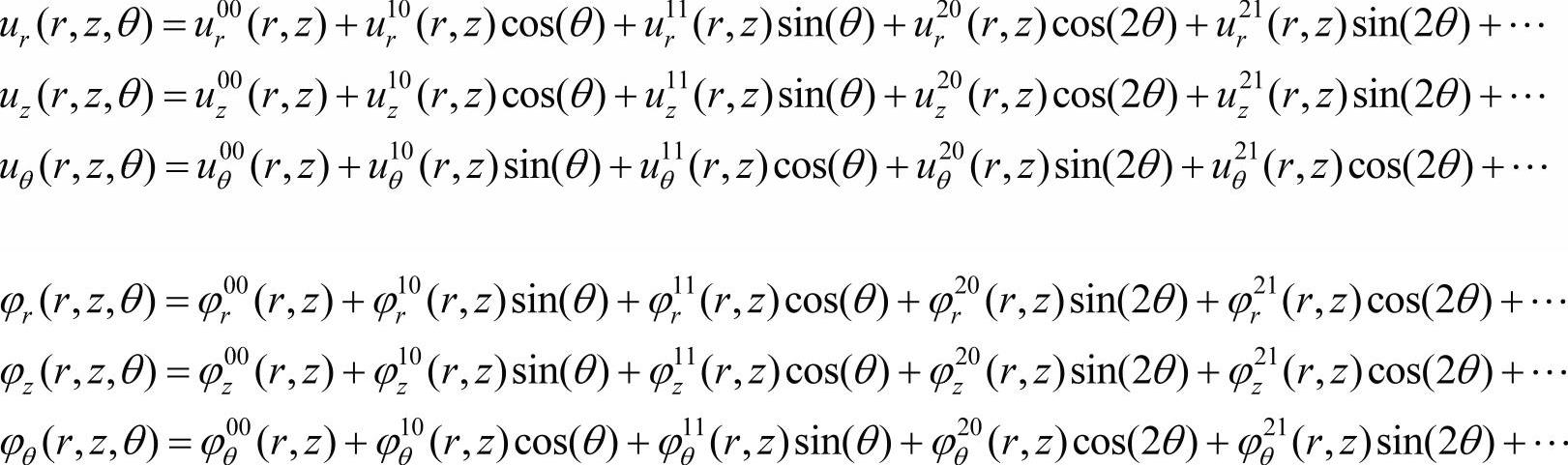
三维(3D)模型:用体单元(六面体、棱柱或者四面体)或者壳单元描述转子系统(见图13-5)。

图13-5 三维转子模型
当需要加速计算时,就会想到简化转子模型,这可以通过超单元实现。(www.chuimin.cn)
位移场可以通过自由度矢量q描述,在惯性坐标系中,惯性力是通过动能的离散表达式得到的。
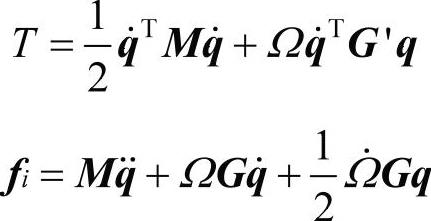
其中,M是质量矩阵;G是陀螺矩阵;Ω是相应转子的角速度。
由于转子和支撑设备的弹性,陀螺效应随着转子向量的方向而变化。按照前面的规定,旋转速度是一个将要解决的已知问题。
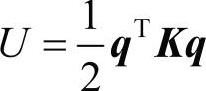
弹性力是通过惯性坐标系里的应变能的离散方程得到的。
fe= Kq
其中,K是刚度矩阵。由于初始装配、离心荷载或者任一其他的荷载存在预应力,弹力就有如下修改:
fe=(K0+Kσ)q
其中,Kσ是几何刚度矩阵,这里的刚度不一定非要各向同性,但是为了保持常数矩阵在圆周的方向,各向同性是需要的。
如果假设有黏性阻尼,阻尼力通过分散函数来表达。
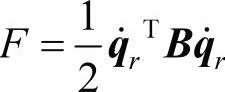
其中,qr是旋转坐标系里的广义位移。在惯性坐标系里,得到的黏性阻尼力有如下形式: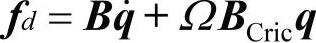
其中,B是黏性阻尼矩阵;BCirc是补充阻尼或者循环力矩阵。
通常,旋转组件中的阻尼和装配时的摩擦力有关。黏性模型就不适合了,滞后模型是比较适合的。滞后阻尼的数学表述仅在频域有效。在时域里描述阻尼行为的一种方法是用可变的黏性阻尼。在这种情况下,黏性阻尼力就可以写为:
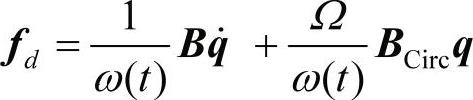
注意这种方法是近似的,更好的方法就是在装配阶段包含摩擦力。





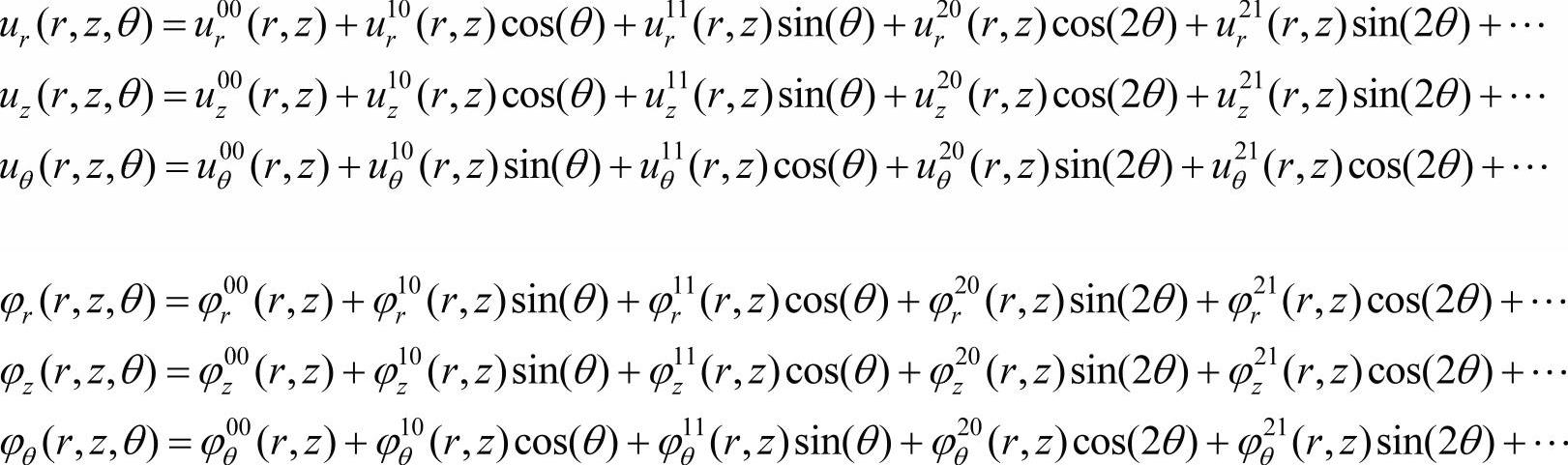

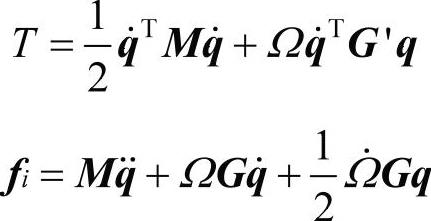
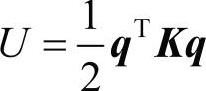
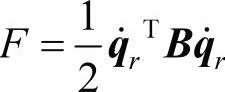
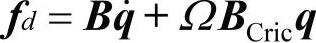
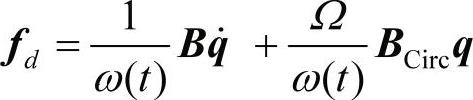






相关推荐