首页理论教育拉普拉斯变换概念及定义

拉普拉斯变换概念及定义

2023-10-26 理论教育版权反馈

【摘要】：知识要点一、拉普拉斯变换的概念1.拉氏变换的定义：设函数f（t）的定义域是t≥0，如果广义积分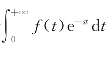对于s在某一范围内收敛，则积分为f（t）的拉普拉斯变换，记作F（s）.即也用记号L［f（t）］表示，即：L［f（t）］=F（s）.其中F（s）叫做f（t）的象函数，f（t）叫做F（s）的象原函数，若F（s）是f（t）的拉氏变换，则称f（t）是F（s）的拉普拉斯逆变换，记作L-1［F（s）］，即：L-1［F

知识要点

一、拉普拉斯变换的概念

1.拉氏变换的定义：

设函数f（t）的定义域是t≥0，如果广义积分 pagenumber_ebook=46,pagenumber_book=41 对于s在某一范围内收敛，则积分为f（t）的拉普拉斯变换，记作F（s）.即

也用记号L［f（t）］表示，即：

L［f（t）］=F（s）.

其中F（s）叫做f（t）的象函数，f（t）叫做F（s）的象原函数，若F（s）是f（t）的拉氏变换，则称f（t）是F（s）的拉普拉斯逆变换，记作L-1［F（s）］，即：

L-1［F（s）］=f（t）

2.常用函数的拉氏变换：

二、拉普拉斯变换的性质

1.线性性质：

若α，β为常数，且L［f1（t）］=F1（s），L［f2（t）］=F2（s）

则有：　L［αf1（t）+βf2（t）］=αL［f1（t）］+βL［f2（t）］=αF1（s）+βF2（s）

L-1［αF1（s）+βF2（s）］=αL-1［F1（s）］+βL-1［F2（s）］=αf1（t）+βf2（t）.

2.平移性质：

若L［f（t）］=F（s），则有L［ektf（t）］=F（s-k）.

3.微分性质（象原函数的微分）：

若L［f（t）］=F（s），则L［f′（t）］=SF（s）-f（0）

同理：L［f″（t）］=s2F（s）-sf（0）-f′（0）(www.chuimin.cn)

4.积分性质（象原函数的积分）：

若L［f（t）］=F（s），则有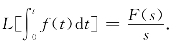 pagenumber_ebook=47,pagenumber_book=42

三、拉普拉斯逆变换

1.一些基本的拉氏逆变换

由象函数F（s）求它对应的象原函数f（t）时，可利用常用拉氏变换及拉氏变换的性质求出f（t）.

2.用部分分式法解象函数.

如果象函数F（s）比较复杂，不能从拉普拉斯变换公式表中直接找到，可采用部分分式法，所谓部分分式就是把一个有理分式分解为若干个最简分式之和的方法，然后逐项从公式表中求出象原函数.

四、利用拉氏变换解常系数线性微分方程的方法和步骤

第一步，对方程两边取拉氏变换，设L［f（t）］=F（s）得出关于F（s）的代数方程；

第二步，解此方程，求出F（s）；

第三步，对象函数F（s）求拉氏逆变换，即可求出微分方程的解.

例题选讲

例1　在拉氏变换定义中以下结论正确的是（　）.

A.f（t）叫做F（s）的象函数　B.F（s）叫做f（t）的象函数

C.F（s）叫做f（t）的象原函数　D.f（t）叫做F（s）的象原函数

解　由拉氏变换的定义，f（t）叫做F（s）的象原函数，F（s）叫做f（t）的象函数.

选BD.