【主要内容】1.级数收敛性的概念设数列{un}，则称记号为无穷级数，简称级数.记，则称{sn}为级数的部分和数列.如果{sn}收敛于s，则称级数收敛，且称s为该级数的和，记为；如果{sn}发散，则称级数发散.2.收敛级数的基本性质（1）如果级数和分别收敛于u与v，则级数和都收敛，它们的和分别为u+v和u-v.（2）如果级数收敛，k为常数，则级数收敛，且当时，（3）如果级数收敛，则在它的前面任意添加......
2023-10-27
常数项级数及性质、收敛与发散判定
【摘要】：知识要点一、常数项级数1.主要概念：常数项级数、收敛、发散、部分和.2.常数项级数的性质：级数收敛的必要条件是级数与其倍乘级数敛散性相同.收敛级数的和差级数也收敛.增减有限项不改变级数的敛散性.收敛级数任意加括号仍收敛，反之不然.3.常数项级数敛散性的判定：判定正项级数的敛散性.①若，则级数必定发散.②利用比值审敛法判定正项级数的敛散性.若un中含有n！
知识要点
一、常数项级数
1.主要概念：常数项级数、收敛、发散、部分和.
2.常数项级数的性质：
（1）级数
收敛的必要条件是
（2）级数与其倍乘级数敛散性相同.
（3）收敛级数的和差级数也收敛.
（4）增减有限项不改变级数的敛散性.
（5）收敛级数任意加括号仍收敛，反之不然.
3.常数项级数敛散性的判定：
（1）判定正项级数的敛散性.
①若
，则级数
必定发散.
②利用比值审敛法判定正项级数
的敛散性.
若un中含有n！，nn，an等因子时，选用比值审敛法比较简便.若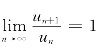
，则改用比较审敛法.
③利用比较审敛法判定正项级数的敛散性.
正项级数的比较法需要用已知敛散性的级数作比较，常用的参考级数有：等比级数（几何级数）
，其中a≠0；p级数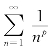
，其中常数p＞0以及调和级数
.必须熟悉上述级数的敛散性.
（2）利用莱布尼兹定理判定交错级数的敛散性.
（3）判定级数绝对收敛与条件收敛.
若级数
收敛，则级数
必定收敛，称为绝对收敛.
若级数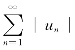
发散，而级数
收敛，则称级数
条件收敛.(www.chuimin.cn)
二、幂级数
1.主要概念：幂级数、收敛半径、收敛区间、收敛域.
2.求幂级数的收敛半径和收敛区间.
（1）不缺项情形，如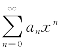
，若设
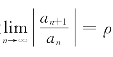，则：
①当0＜ρ＜+∞时，收敛半径
，收敛区间为（-R，R）.
②当ρ=0时，收敛半径R=+∞，收敛区间为（-∞，+∞）.
③当ρ=+∞时，收敛半径R=0，级数仅在x=0点收敛.
（2）缺项情形，如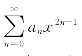
，只需将后项与前项绝对值相比，取极限.若设
则当ρx2＜1时，原级数绝对收敛；当ρx2＞1时，原级数发散.
若ρ≠0，则收敛半径
，收敛区间为（-R，R）；当ρ=0时，收敛半径R=+∞，收敛区间为（-∞，+∞）；当ρ=+∞时，收敛半径R=0，级数仅在x=0点收敛.
在解题时，若仅求收敛区间，可以不讨论端点；若求收敛域，必须讨论端点处的敛散性.
3.求幂级数的和函数.
求幂级数的和函数主要是利用幂级数的运算性质，对级数进行逐项求导或逐项积分等分析运算，把待求和函数的幂级数转化为已知其和函数的幂级数.
4.将函数展开为x或x-x0的幂级数.
利用间接法展开，需要记住ex，sinx，cosx，
，ln（1+x）的展开式，以此作为公式使用，把所要展开的函数作恒等变形或求导、积分化为上述标准公式中的函数形式，而间接展开.
例题选讲
例1 根据级数敛散性的定义判断级数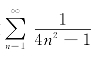
的敛散性，如果收敛，则求其和.
解 该级数的通项可以拆解成两项之差，即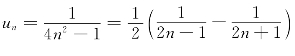
，因此前n项的和
说明：用定义判断级数是否收敛，即判断部分和数列｛Sn｝是否有极限，一般要尽量将通项un拆成两项之差un=f（n）-f（n+1）的形式，以求得Sn，这种方法叫做拆项法.
有关高等数学学习指导的文章
- 详细阅读
- 详细阅读
-
泰勒级数：收敛条件与展开条件详细阅读
泰勒多项式：如果f（x）在点x0的某邻域内具有各阶导数，则在该邻域内f（x）近似等于其中（ξ介于x与x0之间）.如果f（x）存在任意阶导数，且的收敛半径为R，则于是成立的充分必要条件是：当|x-x0|＜R时，，即下面定理成立.定理 设函数f（x）在点x0的某一邻域U（x0）内具有各阶导数，则f（x）在该邻域内能展开成泰勒级数的充分必要条件是f（x）的泰勒公式中余项Rn（x）当n→∞时极限为零，即麦......
2023-10-19
-
常数项级数的概念与规定详细阅读
我们学习初等数学已经知道：有限个实数相加，其结果是一个实数.那么，“无限个实数相加”会出现什么样的结果呢？叫作（常数项）无穷级数，简称级数，记为，即式中的每一个数称为常数项级数的项，其中第n项un叫作级数的一般项或通项.提出问题：有限个数相加得到的是一个确定的和数，而无限个数相加得到的是什么？这需要从极限的观点给出规定.级数的前n项和称为级数的部分和.当n依次取1，2，3，…......
2023-10-19
-
幂级数收敛性及形式-高等数学详细阅读
函数项级数中简单而常见的一类级数就是各项都是幂函数的函数项级数，这种形式的级数称为幂级数，它的形式是其中常数a0，a1，a2，…叫作幂级数的系数.例如：，.注 幂级数的一般形式是经变换t=x-x0就得.对于给定的幂级数，它的收敛域是怎样的呢？......
2023-10-19
-
2015考研数学任意项级数收敛性判别法详细阅读
1.绝对收敛与条件收敛的概念设级数有无穷多个正项，也有无穷多个负项，则称是任意项级数.任意项级数的收敛性分绝对收敛、条件收敛及发散.如果收敛，则称绝对收敛；如果发散，但收敛，则称条件收敛.注 （ⅰ）一般地，当发散时，未必发散.但是，如果由正项级数比值判别法或根值判别法判定发散时，则必发散.（ⅱ）如果绝对收敛，则的收敛性与的收敛性相同.如果收敛，发散，则发散.2.交错级数的莱布尼茨定理设an>0（n=1，2，…......
2023-10-27
-
复数项级数的收敛性及判别法-书籍《复变函数及详细阅读
设{αn}={an+ibn}(n=1,2,···) 为一复数列,表达式称为无穷级数,其前n项的和称为级数的部分和.若该部分和数列收敛,其极限为S,则称上述复数项级数收敛,且称S 为该级数的和,记为若部分和数列{Sn}发散,则称级数发散.定理4 级数 收敛的充要条件是其实部级数和虚部级数都收敛.证明 因其中σn =a1+a2+···+an,τn =b1+b2+···+bn 分别为 的部分和.由定理2......
2023-10-30
-
函数展开成幂级数，求收敛半径R，考查余项极限详细阅读
；写出幂级数，并求出收敛半径R；考查当x在区间内时余项Rn的极限是否为零.如果为零，则函数f在区间内的幂级数展开式为例1 将函数f=ex展开成x的幂级数.解 由fn=ex，得fn=1（n=0，1，2，…......
2023-10-19
相关推荐