解设容器底面半径为r，高为h，则表面积为S=2πr2+2πrh.所以，当容器的高和底直径相等时，所用材料最省.......
2023-10-26
高等数学学习指导：第四章定积分及应用
【摘要】：知识要点一、定积分的概念及性质1.定积分的定义：设函数f（x）是定义在区间［a，b］上连续函数，经过分割、近似替代，求和及取极限的方法求曲边梯形的面积，记作为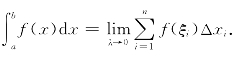2.定积分的几何意义：当f（x）≥0时表示由y=f（x），x=a，x=b与x轴围成的曲边梯形的面积A.如果f（x）≤0时，由于，于是表示曲边梯形面积的相反数，即.如果f（x）在［a，b］上有时为正，有时为负，则等于各部分面积的代数和.3.定积
知识要点
一、定积分的概念及性质
1.定积分的定义：
设函数f（x）是定义在区间［a，b］上连续函数，经过分割、近似替代，求和及取极限的方法求曲边梯形的面积，记作为
2.定积分的几何意义：
当f（x）≥0时
表示由y=f（x），x=a，x=b与x轴围成的曲边梯形的面积A.
如果f（x）≤0时，由于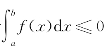
，于是表示曲边梯形面积的相反数，即
.
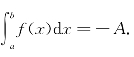如果f（x）在［a，b］上有时为正，有时为负，则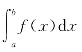
等于各部分面积的代数和.
3.定积分的性质：
对于运算性质，要求熟练掌握，如：
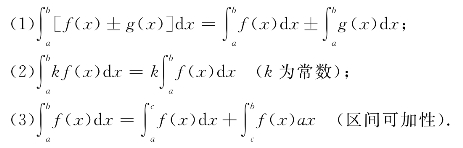
对估计积分值，比较积分大小与积分中值定理等性质理解它的几何意义即可.
4.积分上限函数：
如果上限x在区间［a，b］上任意变动，则对于每个给定的x值，定积分都有一个对应的值，它是定义在［a，b］上的一个函数，称为积分上限函数，记作Φ（x），即
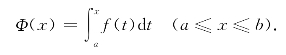
5.积分上限函数的导数：
如果f（x）在［a，b］上连续，则积分上限函数在［a，b］上可导，且
f（x）.
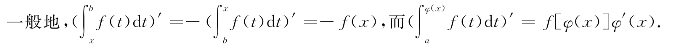
二、定积分的计算
1.牛顿-莱布尼兹公式：
此公式揭示了微分学与积分学的内在联系.
2.定积分的换元积分法：
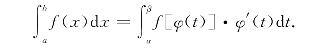
其中x=φ（t）是单调可导的函数.
注意：①应用换元公式时，换元换限.
②如果f（x）在对称区间上，则
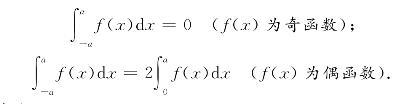
3.定积分的分部积分法：
4.广义积分：
广义积分有无穷区间上的广义积分和无界函数的广义积分，重点是无穷区间上的广义积分，即：
（若两个极限均存在，则广义积分收敛，否则，广义积分发散）.
三、定积分的应用
利用定积分的微元法求解几何、物理、经济等方面的问题，重点是几何应用，即在直角坐标系下求平面图形的面积.(www.chuimin.cn)
一般地，如果函数y=f（x），y=g（x）在［a，b］上连续，且f（x）≥g（x）.则围于两条曲线以及两直线x=a，x=b之间的图形（如图4-1）的面积元素为
dA=［f（x）-g（x）］dx
因此图形面积为
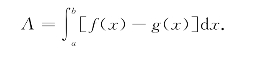
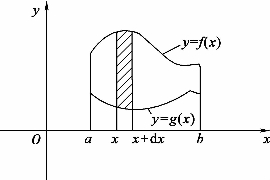
图4-1
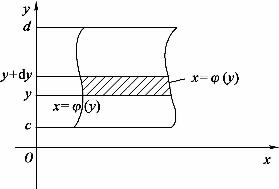
图4-2
同理，如果x=φ（y），x=ψ（y）在［c，d］上连续，且φ（y）≥ψ（y），则由曲线x=φ（y），x=ψ（y）及直线y=c，y=d围成图形（如图4-2）的面积元素为
dA=［φ（y）-ψ（y）］dy
因此图形面积为
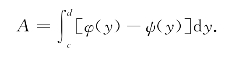
例题选讲
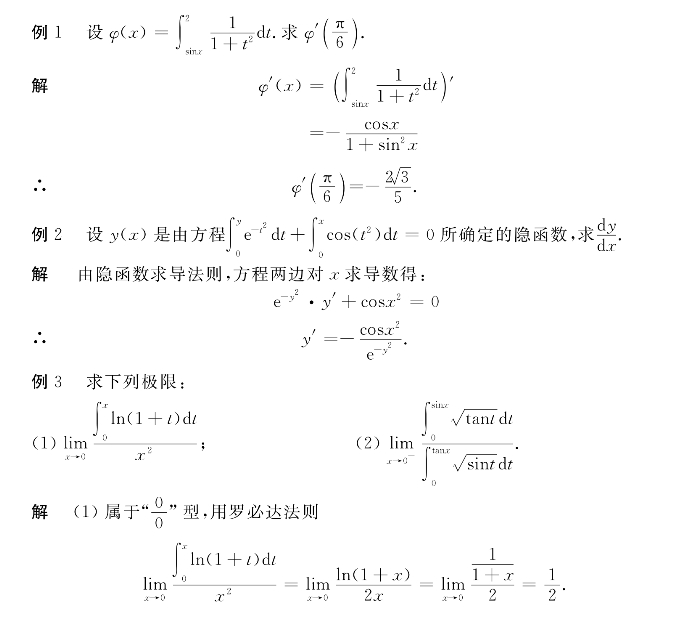
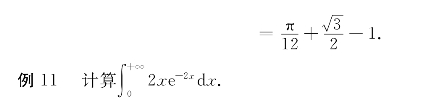
解 本题是无穷区间上的广义积分，由分部积分公式得
例12 求由抛物线y2=x+4与直线x+2y-4=0所围成的封闭平面图形的面积.
解 如图4-3抛物线与直线所围阴影部分的面积.
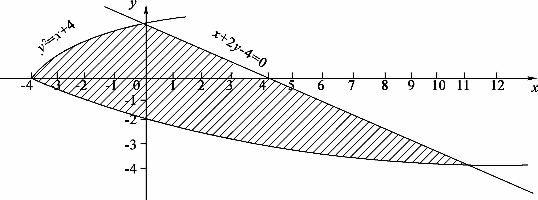
图4-3
首先求交点坐标，由
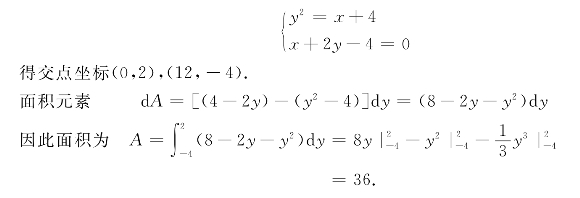
例13 求由曲线y=sinx与它在x=0处的切线和x=2π处的法线所围的图形的面积.
解 方法一：先求y=sinx在x=0处的切线方程
k=y′|x=0=1
∴ y=x.
再求y=sinx在x=2π处法线方程
y=-（x-2π）.
如图4-4围成图形的面积
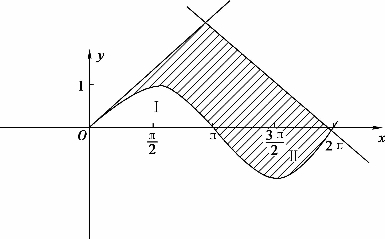
图4-4
有关高等数学学习指导的文章
- 详细阅读
-
高等数学基础：定积分在几何上的应用详细阅读
一、定积分的元素法（微元法）在定积分的应用中，人们经常采用所谓的元素法，为此，回顾一下之前讨论过的曲边梯形的面积计算方法.设f在区间[a，b]上连续，且f≥0，求以曲线y=f为曲边，底为[a，b]的曲边梯形的面积A，如图5.9所示.图5.9（一）分割用任意一组分点a=x0＜x1＜…......
2023-11-20
-
线性代数：高等数学学习指导详细阅读
，kn-r为任意常数，ξ1，ξ2，…解由克莱姆法则知，若所给齐次线性方程组有非零解，则其系数行列式D=0，而由D=0，得λ=1，或μ=0.例6设A，B为n阶方阵，等式（A+B）（A-B）=A2-B2成立吗？......
2023-10-26
- 详细阅读
-
高等数学学习指导：函数、极限与连续详细阅读
知识要点一、函数的概念1.函数、反函数、基本初等函数、初等函数、复合函数的定义.2.理解函数记号y=f（x）中“f”的意义.函数的两个要素，对于两个或两个以上的函数，只有定义域和对应法则完全相同时才是同一函数.3.弄清基本初等函数的概念，熟悉这些函数的特性.4.求f（x）的定义域.对于较复杂的函数求定义域问题，就是求解由简单函数的定义域所构成的不等式组的解集.5.函数的重要性质：有界性，奇偶性，周......
2023-10-26
-
高等数学上册：定积分换元法详细阅读
定理1设函数f（x）在［a，b］上连续，函数x＝φ（t）满足条件：（1）φ（α）＝a，φ（β）＝b，且a≤φ（t）≤b.（2）φ（t）在［α，β］（或［β，α］）上有连续导数.则有公式（5－5）称为定积分的换元公式.证由于f（x）在［a，b］上连续，则存在原函数，在［a，b］上可积.设F′（x）＝f（x），则又｛F［φ（t）］｝′＝F′［φ（t）］·φ′（t）＝f［φ（t）］·φ′（t），于是......
2023-11-19
-
定积分的几何意义-高等数学 上册详细阅读
若函数f（x）≥0，则在几何上表示由曲线y＝f（x）、直线x＝a和x＝b与x轴围成的曲边梯形的面积.当函数f（x）≤0时，由定积分定义知在几何上表示由曲线y＝f（x）、直线x＝a和x＝b与x轴围成的曲边梯形（在x轴下方）的面积的相反数.图5－3一般地，若f（x）在［a，b］上既取得正值又取得负值，则在几何上表示在x轴上方图形的面积减去x轴下方图形的面积所得之差.如图5－3所示，有由几何意义易知，在......
2023-11-19
-
高等数学上册：不定积分性质总结详细阅读
性质1设函数f（x）的原函数存在，k为非零常数，则证因为，所以类似可证明不定积分有下列性质.性质2设函数f（x）与g（x）的原函数均存在，则性质2可推广到有限个函数的情形.利用不定积分的性质和基本积分公式可以求一些简单函数的不定积分.对于不定积分运算需要指出，虽然每个积分号都含有任意常数，但任意常数之和仍是任意常数，所以遇到几个任意常数时只要写一个任意常数即可.例5求解例6求解积分运......
2023-11-19
相关推荐