一、二元函数【知识点回顾】函数的定义：设有两个非空集合M、N，如果当变量x在M内任意取定一个数值时，按照确定的法则f，在N内有唯一的y与它相对应，则称y是x的函数.通常x称为自变量，变量x的取值范围M称为这个函数的定义域；y称为函数（或因变量），变量y的取值范围称为这个函数的值域.【例题1】长方形的面积S与长x（x＞0）与宽y（y＞0）的关系S=xy，当x与y变化时，都有唯一的S值和它对应.【例......
2023-11-20
高等数学学习指导：函数、极限与连续
【摘要】：知识要点一、函数的概念1.函数、反函数、基本初等函数、初等函数、复合函数的定义.2.理解函数记号y=f（x）中“f”的意义.函数的两个要素，对于两个或两个以上的函数，只有定义域和对应法则完全相同时才是同一函数.3.弄清基本初等函数的概念，熟悉这些函数的特性.4.求f（x）的定义域.对于较复杂的函数求定义域问题，就是求解由简单函数的定义域所构成的不等式组的解集.5.函数的重要性质：有界性，奇偶性，周
知识要点
一、函数的概念
1.函数、反函数、基本初等函数、初等函数、复合函数的定义.
2.理解函数记号y=f（x）中“f”的意义.函数的两个要素，对于两个或两个以上的函数，只有定义域和对应法则完全相同时才是同一函数.
3.弄清基本初等函数的概念，熟悉这些函数的特性.
4.求f（x）的定义域.对于较复杂的函数求定义域问题，就是求解由简单函数的定义域所构成的不等式组的解集.
5.函数的重要性质：有界性，奇偶性，周期性，单调性.
6.复合函数的复合过程，弄清自变量、中间变量和因变量.清楚y=f（u），u=φ（x）复合成y为x的函数满足的条件.
二、极限
1.极限的概念.
2.极限的计算方法：
（1）利用极限四则运算法则求极限，要注意该法则是极限都存在的条件下才能使用，当出现
或“∞-∞”等情况，必须对原式进行恒等变换、化简，然后再求极限.
（2）利用两个重要极限求极限：
（3）利用无穷小的性质求极限.
（4）利用等价无穷小代换求极限.
常用等价无穷小量有：当x→0时，sinx～x，tanx～x，1-cosx～
，arcsinx～x，ex-1～x，ln（1+x）～x，（1+x）m-1～mx.
（5）利用函数的连续性求极限（函数在x0点连续，则极限值等于函数值）.
（6）利用极限存在的充分必要条件求极限.
一般地，求分段函数在分界点处的极限时，要考虑左、右极限.
三、函数的连续
1.函数的连续性：
理解连续函数的定义.如果
，则f（x）在x=x0点处连续.
2.间断点及分类：
如果函数f（x）在点x0处不连续，则称f（x）在点x0处间断，点x0称为f（x）的间断点.函数f（x）在间断点的左右极限都存在的间断点为第一类间断点，而f（x）在间断点左右极限至少有一个不存在的间断点为第二类间断点.
四、闭区间上连续函数的性质
1.函数f（x）在［a，b］上连续，则一定有最大值和最小值.
2.知道闭区间上连续函数的介值定理与零点定理.
3.会用零点定理判断及证明函数方程在指定区间中根的存在性.
例题选讲
例1 求函数
的定义域.
解 要使函数有意义，x应满足
∴ 函数的定义域为［1，4）.
例2 设f（x）的定义域是［0，1］，则f（x+1）的定义域是（ ）.
A.［-1，1］ B.［-1，0］ C.［1，2］ D.［0，2］
解 要使f（x+1）有意义
∴ 0≤x+1≤1， -1≤x≤0
∴ 选B.
例3 函数f（x）=ex+e-x的图像对称于直线（ ）.
A.y=x B.y=-x C.y=0 D.x=0
解 该题实际上是判定f（x）的奇偶性.
∵ f（-x）=e-x+ex=f（x）
∴ f（x）为偶函数.由偶函数的特性知图像关于y轴对称.故选D.
说明：判断函数奇偶性的方法主要是根据定义及奇偶函数的运算性质.特别注意定义域的对称性.(www.chuimin.cn)
例4 设
，求f（x）.
分析：可用变量代换法或根据所给表达式直接“拼凑”.
解 方法一：变量代换法
令
，代入原式有
f（t）=1+（t-1）2+（t-1）=t2-t+1
再将t换成x得
f（x）=x2-x+1.
方法二：直接拼凑法
于是 f（x）=x2-x+1 （x≠1）
例5 求下列各数列的极限.
分析：（1）极限呈“∞-∞”型未定式极限，需先分子有理化后，再求极限.
（2）先找到数列前n项和的解析式，再求极限.
说明：在求极限时，经常会碰到极限四则运算不能直接应用，此时需先进行适当的恒等变换化为
型，再通过分子有理化或约去使分母的极限为零的非零因子，从而求得极限.
例7 求极限
分析：由于函数
在x=1处连续，所以可利用函数的连续性求极限.
解 由于f（x）在x=1处连续
说明：如果函数f（x）在点x0连续，可根据
求极限.
例8 求极限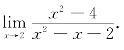
.
分析：本题是
型极限，可先通过分解因式约去致零因子，再求极限.
分析：先需要分子、分母有理化，然后再求极限.
说明：例8、9、10题都是
型极限，求极限常用方法如下：
（1）当函数是有理式时，可通过分解因式消去使分母为零的因式，再求极限；当函数是无理式时，可通过分子、分母有理化消去使分母为零的因式，再求极限.
（2）当函数中含有三角函数时，往往通过三角恒等变形，再利用
求极限，或利用等价无穷小代换法求极限.此方法只能在乘积和商中进行，不能在加减运算中代换，否则会导致错误结论.
例11 当x→0时，ln（1+x）与arcsinx是（ ）.
A.同阶无穷小 B.等价无穷小 C.高阶无穷小 D.低阶无穷小
解 该题是两个无穷小量的比较，实际是求两个函数比值的极限.
∴ 选B.
例12 求下列函数的极限.
说明：本题（1）、（2）属于第二重要极限，利用公式求解.
例13 设f（x）在x=x0处连续，且
.则（ ）.
A.f（x0）可能不存在 B.f（x0）＞1 C.f（x0）＜1 D.f（x0）=1
解 利用函数连续的定义，则f（x0）=1.故选D.
说明：在求极限过程中，要会利用“无穷小量与有界函数之积仍为无穷小量”进行计算.
例17 设
问a，b为何值时，f（x）在（-∞，+∞）内连续.
分析：因为初等函数在其定义域内是连续的，因而要使f（x）在（-∞，+∞）内连续，只需讨论x=0处的情形即可.
例18 证明：方程x·2x=1至少有一个小于1的正根.
分析：先设f（x）=x·2x-1.由介值定理的推论（零点定理）加以证明.
证明 设f（x）=x·2x-1
因为f（x）在（-∞，+∞）内连续，所以f（x）在［0，1］内也连续.
又因为f（0）=-1，f（1）=1，
所以至少存在一点ξ∈（0，1），使f（ξ）=0.
故ξ为方程x·2x=1的小于1的正根.
有关高等数学学习指导的文章
- 详细阅读
-
复变函数的极限与连续性详解详细阅读
复变函数和实变函数类似,同样可以讨论函数的极限和连续性,且形式基本上与实变函数一致.现在介绍复变函数的极限概念.定义3 设函数w = f(z)在点z0的去心邻域:0 ＜|z - z0| ＜ρ内有定义.如果存在一个复常数A,使得对于任意给定的ε ＞0,总存在一个实数δ ＞0(δ ＜ρ),当0 ＜|z-z0|＜δ 时,有|f(z)-A|＜ε,我们称A为f(z)当z趋于z0时的极限,记为复变函数极限的几......
2023-10-30
- 详细阅读
-
函数极限与左、右极限关系详细阅读
【主要内容】1.设函数f（x）在点x0的某个去心邻域内有定义，则limx的充分必要条件是注 （ⅰ）对任意ε>0，如果存在δ>0，当0<|x-x0|<δ时有|f（x）-A|<ε.对任意ε>0，存在δ>0，使得-δ
2023-10-27
-
高等数学第2版：二元函数连续性详细阅读
定义3 设二元函数f（x，y）在开区域（或闭区域）D内有定义，P0（x0，y0）是D内的点（或边界点且P0∈D），如果则称函数f（x，y）在点P0（x0，y0）连续.如果函数f（x，y）在开区域（或闭区域）D内的每一点连续，那么就称函数f（x，y）在D内连续，或者称f（x，y）是D内的连续函数.若函数f（x，y）在点P0（x0，y0）处不连续，则称P0为函数f（x，y）的间断点.前面已经讨论过的函......
2023-10-19
-
高等数学基础：连续函数概念及示例详细阅读
一、连续函数的概念在自然界中有许多现象都是连续不断地变化的，如，气温随着时间的变化而连续变化；金属轴的长度随气温有极微小的改变也是连续变化的等.这些现象反映在数量关系上就是我们所说的连续性.函数的连续性反映在几何上可以看作一条不间断的曲线；下面给出连续函数的概念.（一）函数的增量增量的定义，简单说，就是变化后的量减去变化前的量.例如：早晨t1=8时，温度T1=2℃，中午t2=14时，温度T2=12......
2023-11-20
-
一、二元函数极限与连续、偏导数及二阶偏导数计详细阅读
【主要内容】1.二元函数极限与连续的概念设二元函数f（x，y）在点（x0，y0）的某个去心邻域{（x，y）|0<（x-x0）2+（y-y0）2<δ2}（其中，δ是某正数）内有定义.如果动点（x，y）以任何方式无限趋于点（x0，y0）时，f（x，y）总是无限趋于常数A，则称A是点（x，y）趋于点（x0，y0）（记为（x，y）→（x0，y0））时f（x，y）的极限，记为或注 根据定义，可以按以下方法判......
2023-10-27
- 详细阅读
相关推荐