在图领域，广度优先搜索常被用于求解图的最短路径问题中。松弛操作的伪代码如下：2.Floyd算法Floyd算法是一个经典的全源最短路径算法，适用于不包括负环的图，可以应用于计算所有城市之间的交通道路距离问题。Floyd算法利用了上述两个假设之间的关系，该关系依赖于节点k是否是路径p上的一个中间节点。k=0则表示这两个节点是直接相连的，没有中间节点。......
2023-10-26
深度优先搜索在形式化构件装配中的应用
【摘要】：在实际应用中，很多算法都体现了深度优先搜索的思想。图3-2 有向图的邻接表表示2.拓扑排序深度优先搜索的另一个经典应用是对有向无环图进行拓扑排序。这两次深度优先搜索一次运行在图G上，一次运行在转置图GT上。算法计算的结果是深度优先森林，每一个强连通分量对应一棵深度优先树。
许多图算法在一开始都会先通过搜索来获得图的结构，其他的一些图算法则是对基本的搜索加以优化。在实际应用中，很多算法都体现了深度优先搜索的思想。可以说，图的搜索是整个图算法的核心。以下是图的深度优先搜索算法的几个经典的应用。
1.邻接表的创建
对于一个图来说，进行其他操作的前提是要对图运用某种方法表示出来。目前，有两种方法可以对图进行表示——邻接表和邻接矩阵。两种表示方法既可以表示无向图，也可以表示有向图。如果想要建立一个图的邻接表，需要对图中的节点进行遍历，可以采用深度优先搜索对节点进行遍历，然后在进行深度优先遍历的同时，将与节点u所有相邻的节点添加到以该节点为表头的单链表当中去。这样，我们便可以利用深度优先搜索的思想建立一个图的邻接表。一个有向图的邻接表表示如图3-2所示。
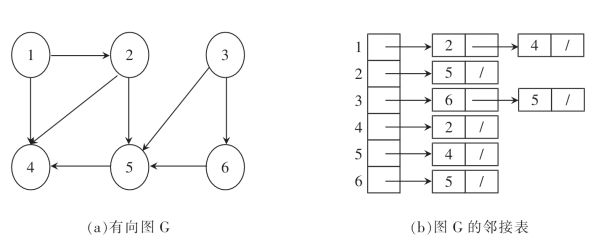
图3-2 有向图的邻接表表示
2.拓扑排序
深度优先搜索的另一个经典应用是对有向无环图进行拓扑排序。如果要对图进行拓扑排序，则要求该图必须是有向无环图。拓扑排序其实就是对一个图中的所有节点进行先后顺序的一个排列。假设在一个有向图G中，节点u是节点v的前驱节点，则在拓扑排序中，节点v在节点u的后面。我们可以简单地把拓扑排序理解为：图中的所有节点都在一条垂直线上按照先后顺序排列好，而边则从上指向下。
在我们的实际生活中，很多事情都需要运用到拓扑排序，如：用拓扑排序表示制作一个生日蛋糕各个步骤之间的先后次序。图3-3描述的是一个人每天早上起床穿衣所发生的事件的次序图。某些服饰必须在穿好其他服饰之后才能穿，比如鞋子必须要在穿好袜子之后再穿。而有些服饰则可以以任意顺序穿上，比如袜子和裤子之间可以以任意次序进行穿戴。对该图进行拓扑排序所获得的就是一种合理穿衣的次序。
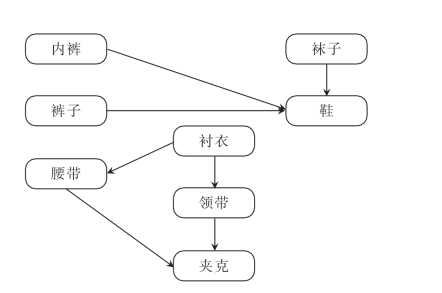
图3-3 拓扑排序实例
下面的简单算法是借助深度优先遍历来实现拓扑排序，这个时候需要使用到栈结构来记录拓扑排序的结果。(www.chuimin.cn)
3.强连通分量的求解
将有向图分解为强连通分量也可以使用深度优先搜索来实现。将图分解为强连通分量是许多针对有向图算法操作的开始。在将图分解为强连通分量后，这些算法将分别运行在每个连通分量上，然后根据连通分量之间的连接结构将各个结果组合起来，从而获得最终所需的结果。
设有向图G=（V，E）的强连通分量是一个最大节点集合C，对于该集合中的任意一对节点u和v来说，路径u到v和路径v到u同时存在，也就是说，节点u和节点v可以互相到达。如在图3-4中，子图｛1、2、5｝是一个强连通分量，｛3、4｝、｛6、7｝、｛8｝也是一个强连通分量。
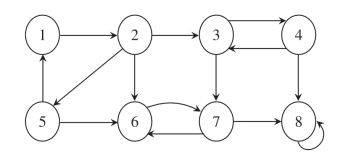
图3-4 有向图G
运用算法STRONGLY-CONNECTED-COMPONENTS能够正确计算出有向图G的强连通分量：
在上述寻找强连通分量的算法中，需要用到图G的转置GT=（V，ET），这里ET=｛（u，v）：（v，u）∈E｝，即ET由对图G中的边进行反向而获得。上述算法使用两次深度优先搜索来计算有向图G=（V，E）的强连通分量。这两次深度优先搜索一次运行在图G上，一次运行在转置图GT上。算法计算的结果是深度优先森林，每一个强连通分量对应一棵深度优先树。
有关形式化构件装配的图算法生成的文章
- 详细阅读
-
生成图算法，形式化构件装配详细阅读
生成式程序设计包括两个开发周期——领域工程和应用工程。应用工程与领域工程不同，开发人员是根据用户的需求开发特定的系统，没有对领域的对象进行抽象。领域工程和应用工程并不存在先后顺序，而是两个并行的过程。生成式程序设计目标集中于特定领域，因此必须要对“领域”这个概念先有一个理解。在领域模型的基础上，设计、开发和组装可复用资源。下面详细地介绍领域工程中的三个不同阶段——领域分析、领域设计以及领域实现。......
2023-10-26
-
形式化构件装配的图算法生成详细阅读
由于本书的研究是PAR方法的一个重要组成部分，故在此，将对PAR方法做较为详细的阐述。图1-1 PAR方法开发过程略图PAR方法是一种基于分划和递推的部分形式化算法程序设计方法，支持算法程序开发的全过程。它包括四个组成部分：算法程序设计方法、基于递推关系的算法设计语言Radl、抽象程序设计语言Apla及一系列转换系统。由PAR方法的理论及上述对算法的推导，我们可以看出，PAR方法在克服软件危机方面将大有作为。......
2023-10-26
-
形式化构件装配图算法生成详细阅读
20世纪80年代以来，形式化软件开发方法的研究及应用为解决上述问题找到了一条有效的途径，使用形式化方法开发软件可以提高软件的可读性、可靠性和可维护性以及软件的开发效率，并为实现软件开发的自动化奠定基础。软件开发的形式化方法是以一般形式化方法为基础的。尤其适宜高安全性系统的开发，这也是形式化方法目前最主要的应用领域。另外，某些形式化方法缺乏描述软件结构的强有力机制，对大型软件的开发不太理想。......
2023-10-26
- 详细阅读
-
定位焊在装配中的应用详细阅读
装配时用定位焊和定位板固定零件时，其强度和刚度的要求是：从装配到焊接的运送过程中定位焊缝不能断开或超过规定的变形，并且有利于减小焊接变形。装配工作中的定位焊，应严格遵守技术文件规定，装配精度应保证技术条件的要求。装配中的点固焊，其长度为20～30mm，间距为300～500mm，焊脚高应为设计高度的一半，且大于4mm。......
2023-07-02
-
元搜索引擎在信息技术书上的应用详细阅读
元搜索引擎由三部分组成，即检索请求提交机制、检索接口代理机制、检索结果显示机制，如图6-6所示。图6-6元搜索引擎的基本结构图①“请求提交”负责实现用户“个性化”的检索设置要求，包括调用哪些搜索引擎、检索时间限制、结果数量限制等。元搜索引擎实际上是一种网络查询接口工具，它的工作原理相对简单。用户向元搜索引擎发出检索请求，它将该请求整理为相应的检索指令发往多个单搜索引擎。......
2023-11-01
-
焊接工艺的重要性在结构装配中的作用详细阅读
在焊接结构生产中，装配-焊接就是通过采用定位器、定位焊或压夹装置将需要连接的零件，按照图样要求连成部件或整体结构，然后再进行焊接的过程。随着焊接结构不断向高度机械化和自动化方向发展，对装配的质量要求越来越高。为了使整个结构焊接后达到质量标准，在制定装配工艺时，必须注明结构的特殊技术要求和公差尺寸，并在生产中严格遵守公差标准。定位焊时不得在非焊接部位随意引弧，重要结构件上不得随意焊接临时构件。......
2023-06-15
相关推荐