叶绿素的英文字典解释截图五十年之后,我并未比当初更加了解生命的真谛。说句老实话,我现在甚至都不能清楚地理解第23题问的究竟是什么。并且,我们还要规定y和v的初始值是什么。抽象的行星椭圆轨道在接下来的十九世纪里,整个电磁学的知识体系因为微分方程的到来,发生了天翻地覆的变化。二十世纪里,类似的情况也曾发生,甚至于量子力学这类伟大发现也受到了微分方程的影响。......
2023-10-26
假如你借给别人一些钱,比如说1英镑(我希望这听上去不要太牵强)。
同时,假设你和借款人通过协商达成一项年利高达100%的协议。这样,在一年后你将获得1+1=2英镑。
但如果你的脑子转得更快(或者更贪得无厌),你也许希望说服借款人同意以每半年50%复利的方式还款。这听上去并无区别——一年两次还款,每次利息为年利的一半,但实际上差别巨大。六个月后,你能得到1+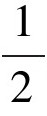 英镑,而再过六个月,你将得到之前任何数额的(1+
英镑,而再过六个月,你将得到之前任何数额的(1+ )倍之多,也就是(1+
)倍之多,也就是(1+ )2=2.25英镑。
)2=2.25英镑。
同样的原理下,如果一年分三次还款,每次利率33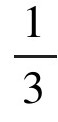 %的情况下,一年的总还款额度为(1+
%的情况下,一年的总还款额度为(1+ )3=2.37,比之前的协议又更胜一筹。
)3=2.37,比之前的协议又更胜一筹。
我们不禁猜想,我们是否能通过这样的方式来赚大钱呢?
很遗憾,答案是否定的。
这是由于当我们不断增加n的值时,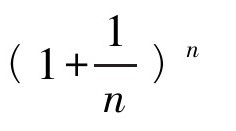 的值慢慢接近一个具体的极限。
的值慢慢接近一个具体的极限。
它的极限是
e=2.718281828459……
就像π一样,这个奇怪的数字e在各种有关数学的场合下不断冒出来。尤其是在那些关于增长率的基础问题上,我们常常需要和它打交道。
y=e t的图像
现在,如果我们有一个变量y,并且随着时间t的变化而变化,其变化速率 通常可以写成一个和y的表达方式不一样的形式。也就是说如果y=t 2,那么
通常可以写成一个和y的表达方式不一样的形式。也就是说如果y=t 2,那么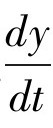 =2t;如果y=sin t,那么
=2t;如果y=sin t,那么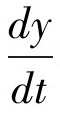 =cos t等等。
=cos t等等。
那么现在问题来了:有没有任何一个变量y,其变化速率永远等于自身的数值呢?
答案是肯定的:
y=e t
这种被称为指数式增长的速度极快。起初,当t=0时,y的值仅为1,但当t=1时,y已经增长了e=2.718倍……当t=2时,y又增长的一个e=2.718倍……如此反复累计。(和整数不一样,当t为分数时,我们可以通过e a×e b=e a+b的方式理解其含义。那么,e 1/2代表e的平方根,因为e 1/2×e 1/2=e 1=e。)
此时,这个特定的e t满足以下条件:
我们可以几乎这么认为,在它具有的所有性质中,以上这个特征将e=2.718……在数学世界里的特殊性一展无余。
这个结果的一个实际运用体现在模拟一种流行病传播的速度上。
设p为在某个时间t时,患病人数占总人口数的比例,并假设此病毒的传播速度和当时已经发病的人口比例成正比,也就是说dp/dt和p成正比:
其中c为常数且大于0。
现在,这个微分方程的解为p=p0 ect,其中p0是当t=0时,最初的患者与总人口的比例。
常数e以这样的方式,进入了我们的视野。根据这个极为简化的模型,推断出来的结果是令人沮丧的:随着被感染人口比例的上升,病毒传播的速度也将越变越快。
另一个我们能常常找到e的地方是整个关于不稳定性的研究。
想象一下,一滴水落在一碗牛奶上,并溅开。起初,这滴水的形状在下降过程中大致是一个球体。由于球体是一个对称的几何图形,我们自然而然地推断碗中牛奶表面也会以大致对称的方式发生变化。(www.chuimin.cn)
牛奶表面溅开的样子
起初,也的确如此:以水滴接触表面的地方为中心,牛奶表面上升并形成一个薄薄的环形牛奶幕墙,并向四面八方扩散开来。
然而在其后很短的时间内,也没有征兆的情况下,牛奶幕墙的顶端就产生了波浪形,一些地方变成的“波峰”,另一些则是“波谷”。这种波状的程度越来越高,特别是那些“波峰”渐渐形成了被拉长的“尖刺”状,最终每一根“尖刺”都掷出一小滴牛奶。
人们不禁会思考,这种“尖刺”状的形态规律到底是从何而来呢?为什么随着牛奶幕墙升高,它无法一直保持对称、匀称的环状外形呢?
答案是,均匀对称的运动的确在理论上有可能性,但我们从未在现实中观察到过它们。现实世界里,总有那么一些不可避免的小“瑕疵”会出现,并快速的扩大其影响,最终导致跟理论上不同的结果。
简而言之,最初那个对称且匀称的运动模式是不稳定的,就好比希望让一支铅笔仅依赖其笔尖来平衡重量,并且矗立不倒。对于当前的讨论,我从这个例子里得到最重要的信息是,在初期,这些运动中产生的小“瑕疵”的影响大小会随着当前已有规模的大小而变化。那么这时:
e=2.718……
就派上了用场。
另一个关于这类讨论的极好的例子存在于下面的图案中——有关化学里的不稳定性讨论。其背景是1951年发现的“贝罗乌索夫——贾勃丁斯基反应。在这个反应中,不同化学物质在空间浓度上的不规则性随着时间的流逝而逐渐变大。在短短的几分钟内,这些化学物质通过自我组织,形成空间波式、有规律的图形。
更多令人窒息的表情
其实,你并不需要一碗牛奶或者一堆不知名的化学物质来理解e=2.718……在实际生活中的应用。
找来两副普通的扑克牌,然后尽量洗牌使牌的顺序打乱,最后将它们并排倒扣在桌上。每次从两堆卡牌里各翻出一张看看是什么花色大小。常识告诉我们,一次出现两张一模一样的几率很小。
两副扑克牌
但如果你不断成对翻开两张牌,寻找“完全一样”的那一对,那么翻完整整52对后,是不是不太可能找到“完全一样”的两张牌呢?
答案是肯定的,我们不太可能找到它们。因为这个几率约等于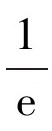 ,小于
,小于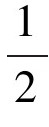 ,也就是小于50%。
,也就是小于50%。
在本章的末尾,我们想展示一下e t的一种令人惊叹的无限数列展开方式:
e t的无限数列展开式
我们也不必仅依靠信任来接受这个结果,因为我们能很容易证明它和之前出现过的关键结果:
背后所运用的原理一致。
为了表现这一点,直接使用本书56页的表格来计算式子中每个单独项的变化速率。
那么,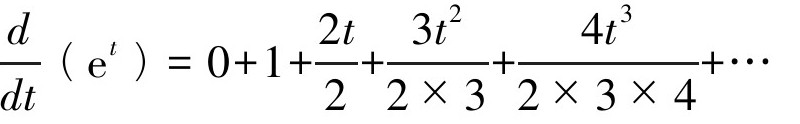 在进行一些必要的化简之后,式子的右侧变为1+t+
在进行一些必要的化简之后,式子的右侧变为1+t+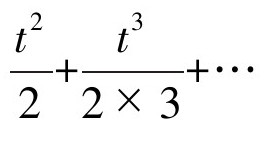 ,跟原式e t的表达方式一模一样。
,跟原式e t的表达方式一模一样。
另一种简单步骤则是将t=1带入到原式中,得到一个关于e的数值本身,且看上去十分优雅的表达方式:
即便如此,相较于本书最后我们将对e做出的诠释来说,这里的结论也会相形见绌。那时,我们会将e放在到目前为止很多人认为是数学里已发现的最伟大的结论中。
有关牛津教授的16堂趣味数学课的文章

叶绿素的英文字典解释截图五十年之后,我并未比当初更加了解生命的真谛。说句老实话,我现在甚至都不能清楚地理解第23题问的究竟是什么。并且,我们还要规定y和v的初始值是什么。抽象的行星椭圆轨道在接下来的十九世纪里,整个电磁学的知识体系因为微分方程的到来,发生了天翻地覆的变化。二十世纪里,类似的情况也曾发生,甚至于量子力学这类伟大发现也受到了微分方程的影响。......
2023-10-26

世间万物,一切皆处于不休的运动中。这里的“物”可以是一个网球拍的位置、一只股票的市值、一根血管中的血压,变化无处不在。数学的各个分支中,和运动联系最紧密的莫过于“微积分”。那么,δt表示一小段时间上的变化。最后的临门一脚解释起来并不容易。这整个过程被称之为“微积分求导”。自从微积分在十七世纪第一次出现,它带来了大量新的研究课题,也彻底改变了数学和物理这两门学科本身。......
2023-10-26

另一方面,不论P点在河岸上哪一点,∠OPH’和∠OPH大小都一样。展开后得到2x-x 2。x(2-x)大小的矩形于是,农场主的这个问题变成了寻找一个x值,使得y=2x-x 2的值达到最大。所以,正方形场地是“最好”的。第一个问题中,这个数代表着P点在河岸上的坐标,第二个问题中,这个数代表x的大小。假设,我们一共只有四座小镇,并为了方便起见,将它们安排在一个长度为1的正方形四个顶点上。简单路网ABCD但这个答案显然不是最短的。......
2023-10-26

用切割矩形的方法估算曲线下面的面积在这个例子里,我们再次碰到了一个永远“没有终点”的数学问题。一旦我们开始正式讨论数字本身的时候,无穷的问题便随之产生了。在数学世界里,“无穷”的概念能在构建逻辑思维中起到重要的作用。截至现在,所有的列车都已经连了起来,最后一步便是发动引擎。数学归纳法的适用范围非常广泛,在不同的应用中,在数学不同的分支中,哪怕是在最深奥的领域里,它一次又一次向人们展现了其价值。......
2023-10-26

最后,再将这个差值首尾对调,并且与原差值相加:495+594=1089。经过这一番操作,我们得到了最终的答案1089。在我的印象中,这个名为“1089”的小把戏是第一个让我觉得不可思议的数学谜题。当我第一次在1956年的“I-SPY”年刊上读到它时,我才10岁。也许正因为那一丝丝神秘感和不可捉摸,使“1089”这类数学谜题同我们当时在学校里学的那些数学知识大相径庭。[1]与“1089”一比,我想你就能理解为什么我会为后者着迷。......
2023-10-26

使用反证法来描述这个问题就是一种令人信服的方式。科尼斯堡地图那么,假设这样的一条线路确实存在。可惜的是,在科尼斯堡的地图上,没有任何一块区域符合这个条件。科尼斯堡现已更名为“加里宁格勒”,受到二战后重建的影响,当地的桥也只剩下五座。都是质数,但15这个可以被3和5整除的数则不是。这次,欧几里得找到了答案:质数的数量是无穷无尽的。但事实上,这是不可能的。......
2023-10-26

反过来,这个关系也几乎成立,除了一点儿“不完美”。即便如此,还是有些特殊的“振动模式”会引起我们的注意。有一种最简单的振动,被称之为“基础模式”。第二谐音同理可得,“第三谐音”以基础谐音三倍的频率振动,整个弦上有两个节点。以第二谐音为例,正确的触碰位置是弦的中点,大概在吉他指板上第十二品丝附近。与此相似,轻触第七或者第十九品丝将使琴弦发出第三谐音。......
2023-10-26

羊胜和公孙诡都是邹阳的朋友,他们也都是有才之人,但是羊胜嫉妒邹阳的才华,几次在梁孝王面前说他的坏话,终于有一天,梁孝王信以为真,下令将邹阳关进监牢,准备处死。邹阳十分激愤,他不甘心就这样被人陷害,于是,他在狱中给梁孝王写了一封信,信中列举事实说明:待人真诚就不会被人怀疑,纯粹是一句空话。梁孝王读了邹阳的信后,很受感动,立即把他释放,并作为贵宾接待。朋友也是要讲究缘分的。......
2023-08-26
相关推荐