牛津教授教你16堂妙趣数学课：马尔法蒂问题的伟大错误解法

2023-10-26 理论教育版权反馈

【摘要】：马尔法蒂的解法在其后的一百年间，大家都认为这个问题已经找到了完美的解决方案。虽然这个问题并不太重要，但它在不少知名数学家手中转了一圈，似乎大家都对马尔法蒂的解法相当满意。然而，在1930年，有人发现一件怪事：如果面对一个全等三角形，马尔法蒂的解法是错误的。马尔法蒂问题的正确解法另一方面，即便是伟大的数学家们也可能得到错误的结论。

从总体上看，数学家是一群十分谨慎的人。

相传有这么一个故事，说的是有一位天文学家、一位物理学家以及一位数学家同乘一列火车，火车奔跑在苏格兰的田野上。这时候他们的窗外出现了一只黑色的绵羊，吸引了三位的注意。

在座的天文学家不禁感叹：“真有趣！原来全苏格兰的羊都是黑色的！”

物理学家听后对这个说法表示感到疑惑，纠正道：“你的意思难道不是有些苏格兰的羊是黑色的吗？”

一旁的数学家听完他们的对话，觉得他们都太冲动，缓缓说道：“我觉得你们俩的意思是，在我们目光所及的这一片的苏格兰境内，至少有一只羊是黑色的。”

这个笑话背后有它深刻的意义：在数学世界里，人们特别容易得到错误的结论。

历史上出现的典型就是马尔法蒂问题。一位名为马尔法蒂的数学家提出了一个问题：在已知的三角形里，如何画三个不相交的圆形，让三者的面积之和最大？

这是一个典型的装箱问题，马尔法蒂本人在1803年将它提出之后，他马上认为自己已经找到了答案：如果你能保证每个圆都和三角形两条边相切，同时与另外两个圆相切，那么这就是你想要的答案。

马尔法蒂的解法

在其后的一百年间，大家都认为这个问题已经找到了完美的解决方案。虽然这个问题并不太重要，但它在不少知名数学家手中转了一圈，似乎大家都对马尔法蒂的解法相当满意。

然而，在1930年，有人发现一件怪事：如果面对一个全等三角形，马尔法蒂的解法是错误的。

马尔法蒂的解法之全等三角形

按照他的说法，答案应为三个圆形的总面积占整个三角形的比例是：

但如果你换个方式调整和排列三个圆形，能得到一个更好的答案：首先画一个三角形内面积最大的圆，然后在剩下的区域内塞下两个较小的圆：

非马尔法蒂的解法之全等三角形

这个答案稍稍超过马尔法蒂的方案所得出的大小。

时间又过了36年，1965年，霍华德·伊夫斯发现了更奇怪的事情：当面对一个整体修长的三角形时，马尔法蒂的解法很容易出错。

马尔法蒂的解法之长条三角形

看上去，无需通过任何计算，我们就能发现三个并排的圆形拥有更大的总面积。

非马尔法蒂的解法之长条三角形

最后，当时间来到1967年，迈克尔·高德伯格向世人展示了，不论针对什么样的三角形，马尔法蒂的“解法”一直都是错的。正确的答案则是：永远都先取三角形内与三边相切的最大圆形。

马尔法蒂问题的正确解法

另一方面，即便是伟大的数学家们也可能得到错误的结论。

1753年，欧拉证明了，没有任何一组整数a, b，c能满足以下式子：

a3+b 3=c 3

也就是说，当我们只能选择整数时，没有任何两个整数的立方和等于另一个整数的立方。眼尖的你可能发现，这是我们在本书第23页见到过的“费马大定理”中的形式之一。

但就在几年后，欧拉相继提出“三个整数的四次方之和也不可能是另一个整数的四次方”“四个整数的五次方之和也不可能是另一个整数的五次方”“五个整数的六次方之和也不可能是另一个整数的六次方”等等一系列假设。(www.chuimin.cn)

很快，人们不断用越来越多和越来越大的数字来对欧拉这一系列猜想进行验证。然而，很多年过去了，没人能找到一个反例证明欧拉的想法是错的，但也无法证明他的结论是对的。

直到1966年，在欧拉提出他的假设大概200年后，L.J.兰德和T.R.帕金终于找到了一个反例，四个整数的五次方之和可以是另一个整数的五次方：

27 5+84 5+110 5+133 5=144 5

如此看来，数学里的一些错误猜想可能会隐藏很长时间而不被发现。

数学中有一个特别的领域为人们埋下了无数的小陷阱，稍有不慎便会失误连连，这便是无限数列。

让我们来看看如下这个无限数列：

事实上，它收敛于0.693……

但如果我们将这个数列中的项数的顺序稍做调整，把每一项正数后面都安排两项负数的话：

这里得强调的是，原数列中所有的项都还保留着，我们既没有漏掉谁，也没有悄悄加入那些本来没有的项。

既然如此，那么整个数列的和看似应该没有什么变化。

但如果你仔细看看，将式子简化一些，并将每一项重新排列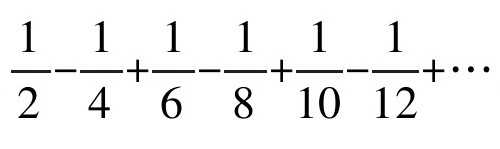，将会得到：

通过交换一些项数的位置，好像我们直接把整个数列的和变成了之前的一半！

这就是真实发生的情况。如果你手中是一个有限数列，那么项数的前后顺序对求和并没有影响，若是将这个结论使用到无限数列上，就大错特错了。

通过将条件推向极端情况的方式，我们能大概感受一下这其中的困难。假设，我们决定首先将原数列中的正数都加起来：

然后再考虑所有负数的问题。这里的难题在于，这一串由正数组成的无限数列并不收敛于任何数，即，它的和是无限大的。当我们的目光转向所有由负数项组成的那部分时，也会遇到同样的困惑。

即使有上面两个结论的铺垫，当我们面对1854年黎曼得出的结论时，也很难压抑我们心中的惊讶。他证明原无限数列可以通过调换各项的位置，达到使之收敛于任意数的目的。

综上所述，当我们解决数学问题时，要时刻小心那些暗处的陷阱，否则我们很容易得到错误的答案。

除此之外，还有些更狡猾的问题等待着数学家们——那些根本无解的问题。

其中有一个例子颇为有趣，它被称为“挂谷问题”，它是由日本数学家挂谷宗一于1917年提出的。挂谷问题的数学描述是：选择长度为1的一根小针头，使其做平移或者旋转，在经过180°回到原位之间，所扫过的面积最小是多少？

从表面上看，这个问题的条件十分简单。大多数人脑海里第一个答案恐怕都是一个半径为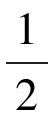的圆。这样的移动非常直观，得到的小圆面积为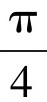，约为0.78。

经过一番思考，我们可以通过一个高为1的全等三角形，来优化我们的答案。秘诀在于，每当小针头绕着自己的一端旋转60°之后，就换到绕另一端旋转60°。现在，扫过的面积减小到，约为0.58。

挂谷问题解法1至3

更佳方案是一个被称为内摆线的曲线，由一个半径为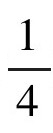的轮子上一个固定点随着整体在另一个半径为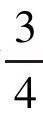的圆圈内部旋转时，所形成的轨迹。最终结果表明，我们所关心的面积减小到只有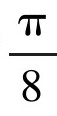，约为0.39。在这么小的面积里，小针头依然可以通过类似“三点旋转“的方式调转180°，回到原位。

在其后的一段岁月里，最后的这个解法被公认为挂谷问题的最佳答案，更小面积是不可能被找到的。

不过，1927年时，A.S.贝斯科维奇宣布这道题没有解，震惊了数学界。他告诉大家，通过恰当的构建方式，小针头扫过的面积要多小就能多小。设定的面积越小，其区域的外形就越接近羽毛状——从中心位置延伸出许多细小的“触手”。

为了给大家一个更直观的解释，让我们想象一个全等三角形被分成了许多等高的三角形，将它们聚拢在一起，使它们部分交叠在一起。最终，人们发现，只要将原三角形分割的次数足够多，就能得到一个足够小的总面积。这个最终的图案命名为“柏龙树“。将几个这种“树”拼接在一起，就能使小针头旋转整整180°。

牛津教授教你16堂妙趣数学课：马尔法蒂问题的伟大错误解法

相关推荐