牛津教授的16堂趣味数学课：揭秘圆周率的历史与解法

2023-10-26 理论教育版权反馈

【摘要】：当人们第一次接触到圆周率π=3.14159……但第二个面积公式，πr2则没那么简单。本书第七章所描述的微积分方法，可以解决这个问题。自从微积分在十七世纪中叶的崛起后，整个计算圆周率的方法都发生了根本性的变化。在此之后不久，莱布尼茨发表了他著名的无限数列：莱布尼兹的圆周率数列这个数列将π和奇数联系起来。如果，你能满足于只采用小数点后一位或者两位小数，也许一个利用概率的圆周率求法显得更简单有趣。

当人们第一次接触到圆周率π=3.14159……的时候，它总是跟圆有关。特别是当一个圆的半径r已知的情况下，其周长则为：

2πr

而它的面积则为：

πr2

通过第一个式子，我们大致能定义π。圆有一个很容易观察到的特征，即是其周长和直径成正比，对于所有的圆来说，是一个定值。我们把这个比值用π这个符号来表示。换句话说，我们将π定义为一个常数，当我们用半径的两倍，也就是直径与之相乘后，答案就是圆的周长。

但第二个面积公式，πr2则没那么简单。在上文为π做出的定义中，丝毫没有提及任何面积。于是，我们的脑子里自然而然地产生了一个简单却又不直观的问题。

为什么第二个公式也是正确的呢？

让我们从一个圆的内接N边形开始讨论。

圆内接八边形

如图所示，这个N边形里将包含N个等腰三角形，比如说OAB（O点是圆心）。而每一个三角形的面积都是其底边AB乘以高h，最后乘以。于是整个N边形的面积则是每个三角形的N倍，写作。同时，（AB）×N是这个N边形的周长，于是我们得到：

若是N的数值变得越来越大，代表这个多边形的边数越来越多，同时每段边长越来越短，而它的形状也更接近一个圆。

N越来越大的N边形

沿着这条路走下去，多边形的周长将无限接近圆的周长，也就是2πr，同时h也将无限接近圆的半径r，其面积也就慢慢接近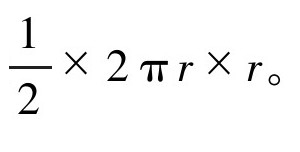也就是为什么圆的面积公式为πr2。

π的实际用途当然还有很多。

就拿一个圆柱形的速食汤罐头为例，其底面半径为r，高度为H。π毫不意外地会出现在它的表面积以及体积公式里。

罐头的表面积和体积

我们马上意识到，这里蕴涵着一个经济问题。如何在保证容积不变的情况下，用最少的材料来制作这个罐头呢？尤其是为了减少表面积时，到底应该选择一个瘦长形的方案，还是一个矮胖形的方案呢？

本书第七章所描述的微积分方法，可以解决这个问题。最终结论是：当2r=H（底面直径和高度相等）时，罐头在保证容积不减小的情况下，表面积最小。

然而有意思的是，我发现家里厨房中所有装玉米粒的罐头都拥有和这一模一样的形状，但所有装汤的罐头却不遵守这个规律。

直到现在，我还没弄明白这到底是为什么，不过没关系，反正π跟汤其实也没多大关系。大而化之，π和圆其实也没多大关系。

事实上，π在数学里也随处可见，即使在那些完全没有圆的地方，我们也能看到它。

想知道π到底是什么，不妨让我们跟随历史的脚步，看看那些为了得到π的精确值所做的努力和尝试。

最早可考证的对π的估算来自成书于公元前1650年的《莱茵德古本》，它将π估算为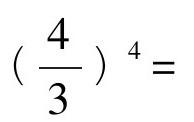3.16……尽管如此，简单将π当作3的做法，在古代世界里被沿用了很多年。甚至，它还曾出现在《圣经·旧约》里：(www.chuimin.cn)

……他又铸造了一个充满炙热铜水的圆形大海，其直径为十肘……绕其一圈，长度为三十肘。

（列王纪上7：23）

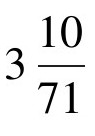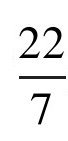历史上第一位试图系统计算π的精确值的人是阿基米德。他用内外各一个边数多达96的多边形，向人们证明：π一定大于，但小于在接下来的几个世纪中，两者中的上限常出现在基本数学课本中，被大家作为π的值来使用。

1593年，数学家韦达找到了用于计算π的精确值的第一个公式：

这个令人赞叹的无限项乘积同样是借助多边形的帮助得到的。其中的平方根给计算带来了一些不便，但它依然让韦达在那个年代精准地算出了π的小数点后14位：

π=3.14159265358979……

自从微积分在十七世纪中叶的崛起后，整个计算圆周率的方法都发生了根本性的变化。在新的方法下，较早出现的一个圆周率计算公式也是无限项乘积的形式：

它是由约翰·沃利斯于1655年发现的。与韦达的做法不同的是，沃利斯的方法并不包含。同时，我们也可以看出公式中的每一项都不断更加接近于1，同时也导致整个乘积慢慢收敛于一个固定值。

在此之后不久，莱布尼茨发表了他著名的无限数列：

莱布尼兹的圆周率数列

这个数列将π和奇数联系起来。不过，我们知道，后来印度喀拉拉学派数学家们在莱布尼兹之前150年左右，就已经发现了相同的公式。只不过他们用一种相当不一样的形式将其表述出来。

莱布尼兹1674年的论文节选，大意为“上帝热爱奇数”

虽然这个数列简单易懂，但若是用它来计算π的精确值，效率十分低下，几近无用，因为它收敛的幅度和速度实在是太小太慢了。计算完前300项所得到的值，尚不如2000多年前阿基米德算出的近似值令人意想不到的是，另外一个无限项数列也包含π：

这是欧拉于1736年时用一个极为“莽撞”的方法获得的结果。

时间滚滚向前，来到欧拉生活的年代时，人们通过各种不同的方法已经将π计算到小数点后约100位。1761年，数学家朗伯证实了大家一直以来都怀疑的结论：π是个无理数，所以无法表示成两个整数相除的形式。这意味着π的精确值是一个无限不循环小数。即便如此，现代的大型计算机依然将π计算到了小数点后几十亿位。

如果，你能满足于只采用小数点后一位或者两位小数，也许一个利用概率的圆周率求法显得更简单有趣。

拿出一张空白的纸，在上面横向画出等距位d的平行直线，并把长度也为d的大头钉随意散落在纸面上。那么，这些大头钉压中某条直线的概率是2/π。

莱昂哈德欧拉（1707-1783）

白纸与大头钉

找不到大头钉？那你也可以尝试扔几次硬币（其实不止几次，是很多次）。如果你扔了总数为2n次硬币（n特别大），那么你得到n次正面和n次反面的概率大致等于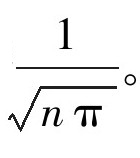也没有硬币？那你还可以让两位朋友各选择很多整数，那么任何随机抽取的两个正整数之间没有除1以外的公因数的概率是6/π2。

这些都似乎和很不一样。

牛津教授的16堂趣味数学课：揭秘圆周率的历史与解法

相关推荐