计算机网络中的路由选择及其可靠性

2025-09-30 理论教育版权反馈

【摘要】：该算法简单，但不适应网络拓扑变化，而且一旦被选路由出现故障，影响信息正常传送，故可靠性差。显然这种方法提高了可靠性，适用于拓扑结构不太复杂的小型网络。有必要讨论一下如何计算的问题，这里的已知条件是整个网络拓扑和各条链路的长度。

在大部分的通信子网中，如果本地端和目的端不在同一个网络中，分组的整个发送过程要经过多次转发，所以存在有路径选择问题。路径选择的算法和它们使用的数据结构是网络层设计的一个主要对象。

路径选择算法负责确定所收到的分组应传输的外出线路，是网络层软件设计的一部分。无论是为每个分组单独地选择路径（数据报情况），还是仅当建立新连接时选择路径（虚电路情况），我们都希望路径选择算法具有正确性、简单性、健壮性，要能妥善解决拓扑结构和通信量变化时不致使主机内的作业夭折，或者出于某个节点IMP（接口信息处理）崩溃而需重新启动网络；还要保证所选路径的稳定性、公平性以及最优性。通常我们把路由选择算法分为两大类：一类是非自适应路径选择算法，有洪泛法、有选择的洪泛法、固定路由法、随机走动法和分散通信法等策略；另外一类是自适应算法，有孤立的路由选择、分布式路由选择、集中式路由选择和混合式路由选择等策略。

1.固定式路由选择算法

它是在网络中每个节点中都存放一张事先确定好的路由表。该表给出从本节点到各自节点的最短路由。当信息报文需要从该节点发送时，可按目的节点从路由表中选出其路由。该算法简单，但不适应网络拓扑变化，而且一旦被选路由出现故障，影响信息正常传送，故可靠性差。为此可在路由表中列出各节点到目的节点的所经路由，若最短路由故障，则选择另一条路由（例如次短路由）传送。显然这种方法提高了可靠性，适用于拓扑结构不太复杂的小型网络。这里用到了求两个网络节点之间的最短路径的算法。有必要讨论一下如何计算的问题，这里的已知条件是整个网络拓扑和各条链路的长度。同时可以推广到求最小时延或者最小信用的问题，只要各链路的长度改为链路或费用，因此求取最短通路的算法具有普遍意义。针对下面的一个例子，我们采用比较平常的一种算法来计算最短通路，如图3—22所示。

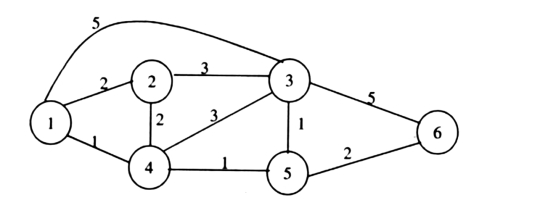
pagenumber_ebook=107,pagenumber_book=101

图3—22　计算最短通路

这里令1节点为源节点，要寻找从它开始到网络中其他各节点的最短通路。令D（v）是从节点1到节点v的距离，是一条通路中所有链路的长度之和。令1（i，j）是节点i到节点j之间的距离。

（1）初始化：网络节点的集合是N，目前只有一个节点，就是节点1。距离计算规则是：如果节点v和节点1直接相连，那么D（v）=1（1，v），如果不直接相连，D（v）就是无穷大。也可以设置为一个比任何通路都大的常数。(https://www.chuimin.cn)

（2）寻优：寻找一个不在N中的节点w，D（w）值为最小，把w加入N集中，然后所有对不在N中的节点，计算［D（v），D（w）+1（w，v）］中较小的值来更新原来的D（v）。不断重复这个步骤，直到所有的节点都在N中为止。

从这张表格可以看出，上述寻优的步骤一共执行了5次，最后得到了以节点1为源的最短通路树。表中画圆圈的数字是每一步中的最小的D（w）。

当然还有其他算法来计算最小通路。

2.距离矢量路由选择算法

这是一种动态路由选择算法，它让每个路由器维护一张表，表中给出了到每个目的地已知的最佳距离和路线，通过与相邻路由器来更新表的信息。这种路由选择算法有时也叫其他的名字，如分布式Bellman—Ford路由选择算法和Ford—Fuiikerson算法。

在距离矢量路由选择算法中，每个路由器维持有一张子网中每一个以其他路由器为索引的路由选择表，表中的每一个项目都对应于子网中的每个路由器。此表项包括两个部分，即希望使用的到目的地的输出线路和估计到达目的地所需时间或距离。所用度量可以为站点、估计的时间延迟（ms）、该路由排队的分组估计总数或类似的值。

计算机网络中的路由选择及其可靠性

相关推荐