首页理论教育测量平差程序设计：误差方程与法方程系数对应关系

测量平差程序设计：误差方程与法方程系数对应关系

2025-09-30 理论教育版权反馈

【摘要】：所以为了节省内存，平差示例程序中采用一维数组保存法方程系数，并且只保存主对角线以上的数值，因而法方程系数阵称为上三角阵。例如pibidi中bi、di在误差方程系数数组中的下标分别是2、4，填充到法方程系数阵二维数组变量中的下标就是（2，4）。

1.误差方程系数、常数储存

误差方程系数临时保存在一维数组nb（）中，以未知数编号为nb（）中系数的下标，误差方程常数临时保存在一个单变量l中。

2.法方程系数、常数储存

法方程系数、常数项分别保存在不同数组中。常数项保存在一个一维数组中，下标是法方程组中方程的编号，即下标为1表明是法方程组中第一个方程的常数。法方程系数阵本是一个对称方阵，由于采用高斯约化解算法方程，实际上只用到对称系数矩阵主对角线以上（或以下）的部分。所以为了节省内存，平差示例程序中采用一维数组保存法方程系数，并且只保存主对角线以上的数值，因而法方程系数阵称为上三角阵。

3.误差方程和法方程系数对应关系

所谓储存对应关系是指根据误差方程系数在数组nb（）中下标，确定其两两相乘元素在法方程系数数组和常数数组中的下标。为方便阐述，设一平差问题只有四个未知数，误差方程一般表达式和系数在数组nb（）中存储位置为：

法方程矩阵式为：

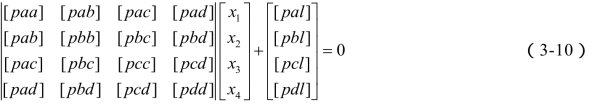
pagenumber_ebook=123,pagenumber_book=116

法方程系数阵二维数组和常数阵一维数组下标编排为：

pagenumber_ebook=123,pagenumber_book=116

分析误差方程和法方程系数、常数在数组变量中的下标编号，可以得出如下结论：

①误差方程系数两两相乘时，误差方程两系数在数组nb（）的下标，就是乘积值所填充到法方程系数阵二维数组变量的下标。例如pibidi中bi、di在误差方程系数数组中的下标分别是2、4，填充到法方程系数阵二维数组变量中的下标就是（2，4）。(https://www.chuimin.cn)

②误差方程系数和常数项的乘积值，填充到法方程常数项数组变量中时，常数项数组中的下标取决于误差方程系数在数组nb（）中的下标。例如pdliii中的di在误差方程系数数组nb（）中的下标是4，所以填充到法方程常数一维数组变量中的下标就是4。

4.法方程系数二维与一维存储的关系

系数阵元素储存在一维数组中，其一维下标和二维数组元素下标对应关系如下：

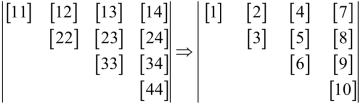
pagenumber_ebook=124,pagenumber_book=117

图3.17　法方程系数阵二维与一维储存数值变量下标对应关系

设i和j是法方程系数阵二维储存时的行号和列号，根据一维数组变量下标的递增方式和图3.17中一维和二维数组变量下标的对应关系，可以归纳出法方程系数一维数组变量下标的计算规律如下：

①主对角线上元素行列号相同，下标计算公式为i（i+1）/2。

②计算j列中数组变量下标应以前一列主对角线元素下标为基础，即以j（j－1）/2为起算值。

③若对各主对角线元素下标加常数k，则按j（j－1）/2+k计算，所得数组变量下标表示的位置均在k行上。

由上述规律可得出根据二维数组变量下标（i,j）计算一维数组变量下标h的公式为：

由此可见，用两两互乘误差方程系数在数组变量中的下标，直接确定互乘值在法方程系数阵二维数组变量中的下标后，就可用公式（3-11）确定其在上三角阵一维数组中的下标。