和高程控制网数据格式一样,示例程序平面控制网数据格式也是只有两种。随之出现的即是已知数据信息。已知数据信息的行数等于已知点数,随着控制网不同而异,但是测站信息就是其结束的标志。作为通用平差程序,要适用于导线网(边角网)、三角网、三边网及各种边角交会图形的混合控制网型,需要分别对lb()、sb()数组进行查询,找出未设过测站的控制点,将其点名加入点名数组dm()。......
2025-09-30
1.推算步骤及数据编排规则
测边三角网坐标推算和测角三角网类似,也是首先要组成三角形,然后按三角形公式解算未知顶点坐标,而且和测角三角形一样,已知点A、B和待定点P必须逆时针排列。三边网观测值是单向水平边长,相对于三角网可根据方向值的大小,识别同一测站方向值间的方位关系,边长观测值没有任何方位信息,因而确定三角形顶点A、B、P逆时针排列是一个复杂而困难的问题。
测量平差程序数据录入编排格式规则越简单,用户使用就越方便,但缺点是会使程序复杂化,影响其可靠性和可读性,甚至可能导致坐标推算失败。而对数据录入格式编排作较严格的规范,固然会使得程序简单化,然而也会因程序使用不便而降低其实用性。平差程序智能化高、使用方便性和其可靠性、可读性本身就是一对矛盾,不可能同时做到最优。因而设计应秉承的原则是权衡利弊,在首先确保程序计算可靠性的基础上,再来减少数据录入的限制。
如图3.5所示顶点分别为1,2,3的测边三角形,一条观测边只能在两个端点中的一个录入,如果不做出限制规定,就可能出现图(a)所示的情况:三条边分别录入在三个测站上。在这种情况下,虽然可以在1号点上查询到观测边照准点是3号点,再从3号点的所有照准点上,或者以3号点为照准点的测站上,依次查询有无观测边照准点为1号点。按照这样的搜索程序,可以组成顶点为1,2,3号点的测边三角形,但是无法保证三角形顶点逆时针排列的关系。
就图3.5(a)所示的情况,确定顶点的逆时针排列顺序并非易事,而与其设计复杂的识别方法解决这个问题,则不如对边长录入设定如下限制:
(1)观测边两个端点都是待定点时,一律记录在两端点中点号较小的测站上;若两个端点中有一个是已知点时,则录入在待定点上。由于测站点号是计算机按读入顺序自动分配的,所以要满足这一要求,实际操作中只要做到在待定点测站上录入观测边数据,并且要录完连接此测站的全部观测边,后续的测站不再重复录入即可。
(2)在一个测站上,观测边依顺时针排列录入。前一条边顺时针旋转到下一条边,必须是能构成三角形的两条边,不能出现像图3.6中测站sb4上,顺时针排列的6、7两条观测边,夹角大于π不能构成三角形的情况。
按此上述规则重新编排数据如图3.5(b)所示,则组三角形算法简单,也不难确定三角形顶点的逆时针排列关系。另外从此例可见,一个测边三角形三条边,两条边录入在同一个顶点,顺时针构成三角形两条边是确定顶点逆时针排列的关键。
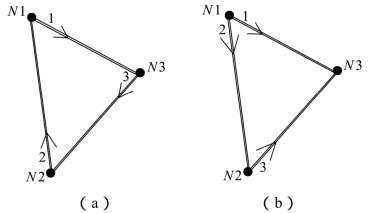
图3.5 测边三角形组成
对于图3.6所示的测边三角控制网,数据录入编排如图上所标注。三角边上的数字表示观测边的全网统一编号,数字靠近哪一个测站点,就表明观测边是录入在哪一个测站下的。下面即以此未严格按规则编排数据的三边网为例,阐述近似坐标推算方法及遇到的问题。

图3.6 三边网数据编排A
①设置第一个点sb1的假设坐标,并假设第一条观测边方向的坐标方位角,以观测边计算照准点sb6的假设坐标。
②依次从测站sb1到sb6,按测站循环组测边三角形。在sb1点上边长观测值1、2顺时针排列,并且边1、2构成三角形的两条边。平差程序调取观测边1、2,并查询到对应的照准点名为sb6和sb3。
③转到测站sb6上查询有无照准点名为sb3的观测边,如没有则再转到测站sb3上,查询有无照准点为sb6的观测边。若点sb6和sb3之间有观测边,则顶点为sb1,sb3,sb6的三角形正确组成,可以根据测边三角形计算出点sb3的假设坐标。
④若没有查到点sb6和sb3之间的观测边,应再进一步查询sb6和sb3是否都是已知点。若是,则两点间没有观测边,可根据已知坐标反算边长组成三角形;若不是,则三角形不能组成。
⑤在测站sb2重复上述步骤,可以组成顶点为sb2,sb3,sb6的三角形,但是点sb2上观测边3、4是逆时针排列的。平差程序不能识别观测边的方位关系。若程序设定观测边号顺时针排列,则三角形顶点排列会不正确,从而导致sb2点坐标计算错误。
⑥测站sb3上只有一条观测边,即使通过搜索能建立测边三角形,也无法确定三角形顶点的逆时针排列。事实上,与sb3有关的两个三角形,顶点坐标已全部算出。程序在组成三角形后,查询到顶点坐标全部算出,会退出三角形解算并循环到下一测站。
⑦测站sb4上观测边号是顺时针排列的,但是边长6顺时针旋转到边长7之间的夹角大于π。程序不能识别观测边的方位关系,按照组三角形的规则,能够组成顶点为sb4,sb2,sb5的三角形。在这个三角形中,边长观测值6、7成为逆时针排列,与程序中观测边顺时针排列的设定相反,所以三角形顶点排列次序不正确。当然在顶点为sb4,sb2,sb5的三角形中,只有sb2一个点假设坐标已算出(计算错误),三角形实际上不能解算。
观测边7顺时针旋转到观测边8,构成三角形的两条边,因而顶点为sb4,sb6,sb2的三角形正确组成,但是由于点sb2假设坐标计算错误,所以点sb4假设坐标计算也是错误的。
⑧在sb5上观测边9、10不构成一个三角形的两条边,虽然观测边9和10,分别可以通过搜索组成分别以(sb5,sb6,sb2),(sb5,sb6,sb1),(sb5,sb4,sb2)为顶点的三个三角形,但是如前所述,不能确定三角形顶点的逆时针排列关系,因而不能保证顶点sb5假设坐标被正确解算。(https://www.chuimin.cn)
通过图3.6所示实例分析可见,要组成测边三角形,并确定顶点的逆时针排列关系,对三边网平差数据编排作严格规定是必要的。不遵守这些规定难以保障三角形顶点的逆时针排列。对于不严格按照规定编排数据出现的问题,通过程序设计来解决不是一件容易的事。即使能够找出处理办法,也会使程序变得非常复杂,因而也是不必要的。
若严格按照前述观测值编排规则,将图3.6中三边网观测数据重新编排如图3.7所示,则测站仅循环到sb2点,坐标即已全部推算完成。

图3.7 三边网数据编排B
图3.8所示是没有将观测边录入在待定点上的实例,根据前述的推算步骤可以看出,对于图3.8(a),程序自动设第一点sb1和sb1点第一条观测边照准方向点sb5的假设坐标。sb1和sb3是已知点,两点间无观测边,坐标推算因三角形sb1,sb3,sb5不能组成而失败。

图3.8 三边网数据编排C
严格执行两端点中若有一个是已知点,观测边录入在待定点上的规定,重新编排数据如图3.8(b)所示,则坐标推算可以顺利完成。
2.测边三角形坐标计算
如图3.9所示三角形ABP中,A、B是已知点,AP、BP方向观测边长是Sb、Sa,求待定点P的坐标。

图3.9 测边三角形坐标计算
根据余弦定律:sa2=s2AB+sb2-2sABsbcosα,得到

根据公式(3-5)求出角α、β之后,即可利用3.6.3小节介绍的自定义前方交会通用过程Intersection(da,db,p,ja,jb)求出P点坐标xP、yP。
3.自定义反余弦函数
VB 系统除了反正切函数外,没有其他反三角函数,因此需要以反正切函数为基础,自定义反余弦函数。设z=cosα=![]() ,则
,则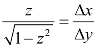 ,反余弦函数以反正切定义为
,反余弦函数以反正切定义为
![]()
4.程序代码


相关文章

和高程控制网数据格式一样,示例程序平面控制网数据格式也是只有两种。随之出现的即是已知数据信息。已知数据信息的行数等于已知点数,随着控制网不同而异,但是测站信息就是其结束的标志。作为通用平差程序,要适用于导线网(边角网)、三角网、三边网及各种边角交会图形的混合控制网型,需要分别对lb()、sb()数组进行查询,找出未设过测站的控制点,将其点名加入点名数组dm()。......
2025-09-30

观测数据的录入按测站进行,首先录入测站名,每个测站名单独占一行,这也是平面控制网数据结构中唯一不带逗号分隔符的数据行。上述数据结构简单易记、无冗余信息。平差计算中需要的已知点数、待定点数、方向观测值数、边长观测值数、测站数、多余观测数等重要信息均反映在数据编排格式中,平差计算程序在录入数据时,可以自行判读或计算出来,因而极大地方便了用户,是测量平差程序数据结构设计的典范。......
2025-09-30

图1.7属性栏②通过程序代码赋值。图1.8访问Label1.Caption属性运行结果访问对象的方法。方法是VB为对象预设的、用户不能更改的事件过程,不同的对象具有不同的方法。前者由滚动条的Value值变化激发,后者在滚动框被拖动时引发。......
2025-09-30

条件方程有两种形式:①直接表示观测值平差值应满足的条件,其一般形式为f()=0,其中表示观测值向量的平差值。②设定一组数目为t的函数独立参数,将所有观测值平差值表示为的函数,其一般形式为=fi()。测量平差中将观测值代入后所得不符值称为闭合差。......
2025-09-30

VB程序是由过程组成的,每个过程是为了完成设定的任务,由一组独立的程序代码组成。图1.11添加过程对话框在“添加过程”对话窗口中只需确定过程名称、类型等信息后回车确定,VB系统即可自动生成“过程”的首尾关键字,用户所需做的工作只是在其中编写代码。......
2025-09-30

Visual Basic 6.0可以创建标准的Windows应用程序、ActveX与Active文档等,在设计阶段,VB通称它们为一个工程。设计VB程序涉及工程与文件的新建、保存、移除等多种操作,这些操作贯穿于创建应用程序的整个过程。工程资源管理器是用来管理工程的,它的功能就像Windows中的资源管理器一样。图1.21工程资源管理器在工程资源管理器中,显示有工程名、工程文件名、窗体名和窗体文件名。工程名为VB对用户所创建的应用程序的标识。......
2025-09-30

1)在中断模式中查看、修改、跟踪出现的错误在中断模式中,用户可以用鼠标跟踪查看相关变量、属性和表达式的值,检查程序运行计算是否存在问题。VB不限制设置断点的数目,被设置断点的语句以紫底白字突出显示。图1.28设置断点2)添加监视调试窗口是VB的重要调试工具,在逐语句运行时可用调试窗口监视表达式和变量的值。“本地”窗口可显示当前过程所有局部变量的当前值,如图1.29所示。图1.29本地窗口立即窗口。......
2025-09-30

FSO对象包含在一个被称为Scripting的类型库中,此库位于Scrrun.dll文件中。表1.1FSO模型对象2.FSO对象应用创立FSO对象。赋值后的对象型变量保存的是所创立对象的引用,即对象在计算机内存中的地址,也称为句柄。表1.2文件夹属性③FSO对象操作文件的方法。Dim fso As New FileSystemObject,ts As textstreamSet ts = fso.CreateTextFile上述语句功能是声明对象型变量,创建文件并赋予文本文件型变量ts。......
2025-09-30
相关推荐