图3.2方位角推算3.坐标转换设有已知点a、b，已知坐标和假设坐标分别为,和, ；边长sab的真实与假设坐标方位角和长度分别为：αab,sab和将假设坐标转换为近似坐标的步骤为：求旋转角：求尺度参数：坐标转换：对于上述坐标转换方法，在此需要作两点说明：①导线网假设坐标推算是采用的实测边长，因而坐标转换本可不设尺度参数，这里设置尺度参数是为使坐标转换函数，也可适用于三角网假设坐标转换。......
2023-10-22
三角网坐标计算-测量平差程序设计 第2版
【摘要】：测边三角网一般简称为三边网，其近似坐标计算方法将在下一小节讨论。如图3.3所示的三角网，组三角形解算坐标的步骤如下：按测站循环。图3.3组成三角形三角形坐标推算采用的算法是前方交会坐标计算方法。三角网近似坐标推算路线和起算点位置、网型结构、观测数据录入顺序等诸多因素有关而无法预测，推算过程中如何保证三角形顶点的正确排列，是平差程序设计中的一个难点。
1.计算方法
在光电测距和卫星定位测量技术广泛应用之前，三角网一直是控制测量的主要网型结构。在当前测量新技术飞速发展的条件下，三角网由于存在观测工作量大、通视条件难以满足的固有缺陷，在大范围控制测量中已经不再采用。但是三角网具有控制面积大，约束条件多，可靠性高，精度高的优势，因而在精密工程控制测量领域仍有应用价值。
三角网分为测角三角网、测边三角网、边角同测三角网三种类型。测边三角网一般简称为三边网，其近似坐标计算方法将在下一小节讨论。边角同测三角网近似坐标可以按导线网方法计算不在此阐述，因此本小节所讨论的三角网是指单纯测角三角网。
按照已知点在控制网中的分布划分，三角网也可以分为两种情况：
（1）至少有一对已知点相连通。
（2）已知点均不连通。
对于前一种情况，可以直接从已知点起算，依次推算待定点近似坐标，而后一种情况，则不能进行这样的推算。如前所述，通用测量平差程序必须要顾及各种可能出现的情况，所以近似坐标计算思路和导线网一样，首先是对任意两个相邻并通视的控制点设置假设坐标，然后以这两个点为起算点，依次推算全部点（包括已知点）的假设坐标。假设坐标推算完毕后，再根据任意一对已知点两套坐标所包含的坐标转换信息，对控制点假设坐标进行平移、旋转、缩放变换，将其转换为实际坐标系统下的近似坐标。
测角三角网坐标计算首先要组成三角形，然后在三角形两个顶点假设坐标已算出的基础上，解算待定顶点假设坐标。计算步骤是作测站、方向二重循环，逐测站、逐方向地组三角形并解算假设坐标。如图3.3所示的三角网（方向连线上的编号是全网统一编排的方向值号），组三角形解算坐标的步骤如下：
（1）按测站循环。
（2）在测站上按方向循环，设方向循环变量为i，依次查询方向值i和i＋1的照准点名。若i已是该测站的最大方向号，则令i＋1为该测站的零方向编号。例如在图3.3所示的三角网，在N2点上查询到方向值4、5照准点名分别是N6和N10，设方向值以Li表示，则三角形顶点N2夹角值为方向值为L5-L4。
（3）在N6测站上按方向循环，查询到有照准N10、N2点的方向值编号分别为21、19，因此三角形顶点N6夹角值为L19-L21。由图3.3可见，方向值L19是零方向，因而计算出的夹角是负值，出现这种情况要对负的夹角加2π。
（4）在N10点上按方向循环，查询到有照准点N2、N6的方向值编号分别为37、38，求的三角形顶点N10夹角值为L38-L37。
（5）经过步骤（2）～（4），组成顶点为N2、N6、N10的三角形。查询三个顶点假设坐标是否已算出。若只有一个顶点假设坐标没有算出，则可调用三角形计算公式求待定点坐标。
（6）若三角形不能组成，或者虽然组成了三角形，但是不满足三个顶点中只有一个假设坐标未算出的条件，方向值循环到下一方向，重复步骤（2）～（5）。(www.chuimin.cn)
（7）一个测站方向值循环完毕，测站循环到下一测站，重复步骤（2）～（6），直至测站循环完毕。
（8）和导线网假设坐标计算一样，对于结构复杂的三角网，一次测站循环可能不能完成全部点假设坐标计算。若循环完毕后经过查询仍有控制点假设坐标未算出，则需要多次重复步骤（1）～（7）。直至全部控制点假设坐标解算完毕，或者虽然仍有控制点未算出，但循环次数已达设定次数，继续循环已无意义为止。
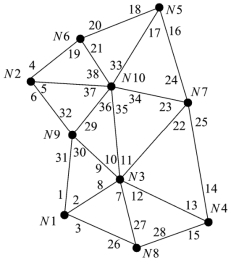
图3.3 组成三角形
三角形坐标推算采用的算法是前方交会坐标计算方法。如图3.4所示，点A、B坐标已解算出，P是待定点，观测角为α、β，点A、B、P按逆时针排列，前方交会计算待定点P的公式为：
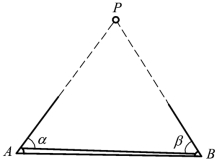
图3.4 前方交会坐标计算
前方交会仅仅观测夹角α、β而没有多余观测，因而没有检核条件。在此基础上P点坐标的解并不唯一，所以点A、B、P逆时针排列是必需的，否则就会得到一个错误解。三角网近似坐标推算路线和起算点位置、网型结构、观测数据录入顺序等诸多因素有关而无法预测，推算过程中如何保证三角形顶点的正确排列，是平差程序设计中的一个难点。为保证三角形顶点的逆时针排列，方向观测值录入顺序必须逐测站按方向值大小依次录入，否则就会造成计算错误。
2.程序代码
有关测量平差程序设计 第2版的文章
- 详细阅读
-
测量平差程序设计：任意组合网坐标计算详细阅读
任意组合网的基本结构是导线网和三角网，因而坐标计算方法实际上就是综合运用单一网型的计算方法。由于任意组合控制网网型复杂多样，存在许多的不确定因素，因而其近似坐标推算非常复杂，是平面网平差程序设计中公认的难点。任意组合网测量平差程序，要求能适用于各种控制网网型结构，因而程序设计必须周密考虑坐标推算可能遇到的情况，包括一些极端的特殊情况。推算路线也是关系到任意组合网坐标推算能否顺利完成的重要因素。......
2023-10-22
-
测量平差程序设计：三边网坐标计算详细阅读
下面即以此未严格按规则编排数据的三边网为例，阐述近似坐标推算方法及遇到的问题。图3.6三边网数据编排A①设置第一个点sb1的假设坐标，并假设第一条观测边方向的坐标方位角，以观测边计算照准点sb6的假设坐标。事实上，与sb3有关的两个三角形，顶点坐标已全部算出。若严格按照前述观测值编排规则，将图3.6中三边网观测数据重新编排如图3.7所示，则测站仅循环到sb2点，坐标即已全部推算完成。......
2023-10-22
-
测量平差的基本概念-《测量平差程序设计第2版详细阅读
条件方程有两种形式：①直接表示观测值平差值应满足的条件，其一般形式为f()=0，其中表示观测值向量的平差值。②设定一组数目为t的函数独立参数，将所有观测值平差值表示为的函数，其一般形式为=fi()。测量平差中将观测值代入后所得不符值称为闭合差。......
2023-10-22
-
测量平差程序设计：对象概念详细阅读
图1.7属性栏②通过程序代码赋值。图1.8访问Label1.Caption属性运行结果访问对象的方法。方法是VB为对象预设的、用户不能更改的事件过程，不同的对象具有不同的方法。前者由滚动条的Value值变化激发，后者在滚动框被拖动时引发。......
2023-10-22
-
测量平差程序设计方程法详细阅读
设有n个观测值，组成误差方程组为：应用最小二乘准则组成法方程组，其纯量形式为：其中法方程系数、常数阵中的数值由此可见自乘系数[paa]是由n个值的和组成，这n个值分别是各观测值误差方程中第一个未知数系数平方乘以观测值的权；互乘系数[pab]也是由n个值的和组成，这n个值分别是各观测值误差方程中第一个和第二个未知数系数之积乘以观测值的权。根据这一特点，平差程序组法方程采用的算法是：①按测站循环。......
2023-10-22
-
测量平差程序设计：工程概念详细阅读
Visual Basic 6.0可以创建标准的Windows应用程序、ActveX与Active文档等，在设计阶段，VB通称它们为一个工程。设计VB程序涉及工程与文件的新建、保存、移除等多种操作，这些操作贯穿于创建应用程序的整个过程。工程资源管理器是用来管理工程的，它的功能就像Windows中的资源管理器一样。图1.21工程资源管理器在工程资源管理器中，显示有工程名、工程文件名、窗体名和窗体文件名。工程名为VB对用户所创建的应用程序的标识。......
2023-10-22
-
测量平差程序设计：过程的定义详细阅读
VB程序是由过程组成的，每个过程是为了完成设定的任务，由一组独立的程序代码组成。图1.11添加过程对话框在“添加过程”对话窗口中只需确定过程名称、类型等信息后回车确定，VB系统即可自动生成“过程”的首尾关键字，用户所需做的工作只是在其中编写代码。......
2023-10-22
相关推荐