对于导线网、三边网,可以依测站按观测边循环,计算边长平差值及其精度指标。所以评定精度的方法是,将边长表示为端点坐标平差值的函数,线性化得到权函数式,然后对此应用协因数传播律求权倒数。......
2023-10-22
1.点位中误差
点在坐标平面中的位置是用一对平面坐标来确定,由于观测存在误差,所以点位坐标也存在误差。在一个确定的坐标系中,设P点为待定点真实位置,P′为平差值位置,P′与P间距离PΔ为P点的点位真误差(见图2.4)。
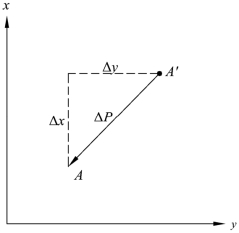
图2.4 点位误差
显然根据几何关系可得:ΔP2=Δx2+Δy2,对此求期望值可得到:
![]()
即P点点位方差等于其x坐标方差与y坐标方差之和。
点位真误差ΔP是由观测误差引起,显然与坐标系统设置无关,因此可以得到结论:点位方差σ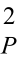 等于点位真误差ΔP在任意两个相互垂直方向上投影的方差之和。
等于点位真误差ΔP在任意两个相互垂直方向上投影的方差之和。
工程实践中得不到真误差,也不可能无限次观测,所以只能得到误差的估值,所以式(2-53)一般表示为:
![]()
式中,待定点纵横坐标中误差计算公式为:

式中,qxixi为未知参数xi的权导数,是未知参数向量X协因数阵QXX主对角线上的第i个元素,qyiyi为未知参数yi的权导数,是未知参数向量X协因数阵QXX主对角线上的第i+1个元素。
由于间接平差法一般直接选择待定点坐标为未知参数(或待定点高程),所以QXX =N-1。例如有s个待定点时,未知数的协因数阵为:

因此,求某一个未知参数的协因数(权倒数),可直接从![]() 矩阵主对角线上提取。
矩阵主对角线上提取。
点位误差是相对于坐标原点的,由于经典平差中已知点是视为没有误差的,所以实际上也是相对已知点的,即我们估算的点位误差均是相对于已知点的。
2.任意方向φ的位差
如图2.5所示,待定点P点位真误差PΔ在任意方向φ投影值为PP′,与PΔ在x,y坐标轴方向投影值,xyΔΔ的关系式为:
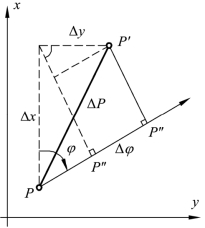
图2.5 任意方向φ的位差
![]()
由于假设P点是没有误差的真实位置,所以真误差,xyΔΔ也是P′点的坐标误差。对式(2-54)应用协因数传播律,求得误差φΔ之中误差权倒数:

式中,qxy是P′点x,y坐标的相关权倒数。根据权导数和单位权中误差求φ方向位差:
![]()
3.方向点位中误差的极大值E和极小值F
由于单位权中误差0m与φ无关,所以φ方向点位中误差mφ的值取决于权倒数qφφ。在式(2-54)中,qiixx,qiiyy和qiixy是常数,因此qφφ是坐标方位角φ的函数。φ的取值范围是0°~360°,以φ为极角,mφ值为极径,按极坐标法绘制点(φ,mφ)的轨迹,得到一封闭曲线称为误差曲线。误差曲线形状接近椭圆,其极径的长度即等于点位中误差在该方向的投影。由式(2-56)及图2.6可见,误差曲线是一对称图形,当0φ=°和90φ=°时,mφ就分别等于mx和my,在坐标方位角为φE的方向,取得最大值E,在与其相互垂直的方向φF,取得最小值F。由于点位中误差平方等于点位中误差在任意两个相互垂直方向投影的平方和,所以有:
![]()
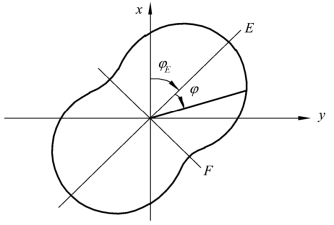
图2.6 误差椭圆曲线
令![]() ,得到-qxxsin2φ0+qyysin2φ0+2qxy cos2φ0=0。整理即得极值解φ0:
,得到-qxxsin2φ0+qyysin2φ0+2qxy cos2φ0=0。整理即得极值解φ0:
![]()
由于tan2φ0=tan(2φ0+180°),所有φ0有两个根,一个为φ0,另一个为φ0+90°,即极值方向有两个,一个是极大值,另一个则是极小值。
确定极值方位的法则是:
(1)qxy>0,极大值在一、三象限,极小值在二、四象限。
(2)qxy<0,极大值在二、四象限,极小值在一、三象限。(www.chuimin.cn)
设极大值坐标方位角为φE,极小值坐标方位角为φF,以E、F表示φE、φF方位中误差mφE 、mφF,则E、F的计算公式为:

由公式(2-62)可以看出:
![]()
4.误差椭圆
点位误差曲线不是一种典型曲线,但是形状上与以E、F为长短半轴的椭圆相似。受当时技术条件局限,测量上长期以椭圆代替误差曲线,称为点位的误差椭圆,长轴坐标方位角Eφ和长短半轴E、F称为点位误差椭圆的参数。椭圆方程为:
![]()
误差椭圆的向径不再是P点在该方向的误差,但只要在垂直于该方向上作椭圆的切线,则垂足与原点的连线长度即该方向上位差。
5.点位落入误差椭圆内的概率
平面控制点的点位是通过一组观测值求得的,由于观测值带有随机误差,求得的点位也是随机点。观测误差服从正态分布,因而二维坐标表示的随机点服从二维正态分布。
二维正态分布的联合密度函数为:
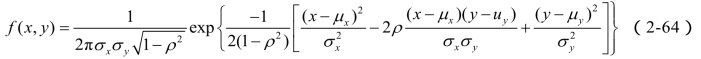
式中,μ,u为随机点x、y坐标的数学期望值,其中xy![]() 为随机变量x与y的相关系数。
为随机变量x与y的相关系数。
f(x,y)的几何图形是图2.7所示曲面,其形状如山冈,在点(μx,μy)上达到最高峰。若用一组与XOY坐标平面平行的平面去截该分布曲面,然后将截线投影到XOY平面上,则得到一族同心椭圆,椭圆中心为(μx,μy),椭圆方程为:

图2.7 f(x,y) 的几何图形

式中,λ2为一常数,同一椭圆上所有点的二维正态分布联合密度函数f(x,y)是等值的,所以这些椭圆称等密度椭圆。当f(x,y)等于不同常数时,同心椭圆反映了随机点点位分布情况,因此被称为误差椭圆。为简便起见,将椭圆中心作为坐标原点,则误差椭圆方程变为:
![]()
由解析几何知,当有方程Ax2+Bxy+Cy2=R2时,为了消去Bxy项,使其变为标准形式,必须将坐标系旋转一个θ角,θ角由下式确定:
![]()
由于ρσxσy=σxy=σ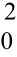 Qxy,σ
Qxy,σ =σ
=σ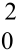 Qxx,σ
Qxx,σ =σ
=σ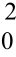 Qyy,即有
Qyy,即有
![]()
于是知旋转角实际上即φ0,即σφ取得极大值或极小值的方向,或者说x,y坐标轴旋转后与E,F方向重合,则椭圆方程式(2-65)即可取得标准化形式。此时在新坐标系中,σ 、σ
、σ 被E2、F2代替,并令λ=k,则椭圆方程为:
被E2、F2代替,并令λ=k,则椭圆方程为:![]() 当k取不同的值时,就得到一族同心误差椭圆并记作Bk。令k=1,则误差椭圆称为标准误差椭圆。
当k取不同的值时,就得到一族同心误差椭圆并记作Bk。令k=1,则误差椭圆称为标准误差椭圆。
经过上述简化后,二维正态分布的密度函数为:
![]()
现在讨论待定点落入误差椭圆Bk(记作(x,y)⊂Bk)内的概率,即

作积分代换,令x2=2E2u2,y2=2F2v2,标准椭圆方程变为:![]() ,这是一个圆方程Ck,待定点落入误差椭圆Bk内的概率现在等于落入圆Ck内的概率,所以
,这是一个圆方程Ck,待定点落入误差椭圆Bk内的概率现在等于落入圆Ck内的概率,所以
![]()
令u=rcosθ,v=rsinθ,则

给定不同的K值,即得点位落入误差椭圆的概率P(见图2.8)。
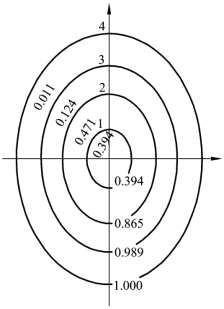
图2.8 点位落入误差椭圆的概率
有关测量平差程序设计 第2版的文章

对于导线网、三边网,可以依测站按观测边循环,计算边长平差值及其精度指标。所以评定精度的方法是,将边长表示为端点坐标平差值的函数,线性化得到权函数式,然后对此应用协因数传播律求权倒数。......
2023-10-22

条件方程有两种形式:①直接表示观测值平差值应满足的条件,其一般形式为f()=0,其中表示观测值向量的平差值。②设定一组数目为t的函数独立参数,将所有观测值平差值表示为的函数,其一般形式为=fi()。测量平差中将观测值代入后所得不符值称为闭合差。......
2023-10-22

未知数数目因控制网性质、图形结构和平差方法不同而计算方法不同。高程控制网必要观测数t为待定点数,所以“多余观测数”=“观测值数”-“待定点数”。以示例程序中的变量表示,则为r=n–导线网。任意组合网既有方向观测值也有边长观测值,所以综合上述几种情况,就有r=nl+ns-2–dxj其中变量dxj是有观测方向值的测站数,其值需要查询统计获得,相应的程序代码为:dxj=0求得了[pvv]和多余观测数r,单位权中误差就可按m0=计算。......
2023-10-22

图1.7属性栏②通过程序代码赋值。图1.8访问Label1.Caption属性运行结果访问对象的方法。方法是VB为对象预设的、用户不能更改的事件过程,不同的对象具有不同的方法。前者由滚动条的Value值变化激发,后者在滚动框被拖动时引发。......
2023-10-22

调用通用过程或函数过程时,出现在过程名后面圆括号里的常量、变量或表达式,称为实际参数,简称“实参”。一般情况下,过程调用时,实参与形参在数量、变量数值类型上必须一一对应。传址比传值效率高,但采用传址方式,形参并不是真正的局部变量,有可能对程序的执行产生不必要的干扰,比如在过程中对形参赋值,就会改变对应的实参值,当然反过来利用这一点,也可以从过程中传递值出来。......
2023-10-22

设有n个观测值,组成误差方程组为:应用最小二乘准则组成法方程组,其纯量形式为:其中法方程系数、常数阵中的数值由此可见自乘系数[paa]是由n个值的和组成,这n个值分别是各观测值误差方程中第一个未知数系数平方乘以观测值的权;互乘系数[pab]也是由n个值的和组成,这n个值分别是各观测值误差方程中第一个和第二个未知数系数之积乘以观测值的权。根据这一特点,平差程序组法方程采用的算法是:①按测站循环。......
2023-10-22

Visual Basic 6.0可以创建标准的Windows应用程序、ActveX与Active文档等,在设计阶段,VB通称它们为一个工程。设计VB程序涉及工程与文件的新建、保存、移除等多种操作,这些操作贯穿于创建应用程序的整个过程。工程资源管理器是用来管理工程的,它的功能就像Windows中的资源管理器一样。图1.21工程资源管理器在工程资源管理器中,显示有工程名、工程文件名、窗体名和窗体文件名。工程名为VB对用户所创建的应用程序的标识。......
2023-10-22

VB程序是由过程组成的,每个过程是为了完成设定的任务,由一组独立的程序代码组成。图1.11添加过程对话框在“添加过程”对话窗口中只需确定过程名称、类型等信息后回车确定,VB系统即可自动生成“过程”的首尾关键字,用户所需做的工作只是在其中编写代码。......
2023-10-22
相关推荐