图9-21 目标偏心误差3.整平误差整平误差是指安置仪器时竖轴不竖直产生的误差。......
2023-08-20
平面控制网观测值误差方程分析
【摘要】：列角度观测值误差方程，求角度误差方程系数和常数项。
1.角度观测值的误差方程
如图2.2所示，j, k是两待定点，近似坐标为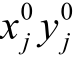
,
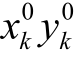，根据近似坐标求得近似边长为
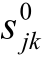，近似坐标方位角为
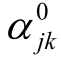。设近似坐标改正数为δxj, δyj, δxk, δyk 。近似坐标方位角改正数δαjk。根据坐标方位角与端点坐标关系式得
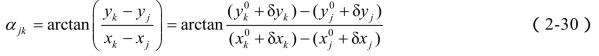
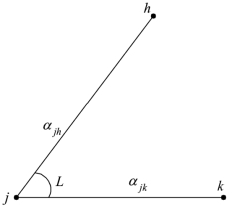
图2.2 观测角与坐标方位角
将式（2-30）按泰勒级数展开，取至一次项得
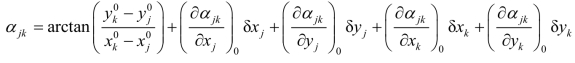
令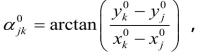
则
同理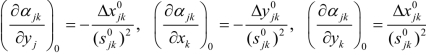
由于δαjk的单位为秒，故
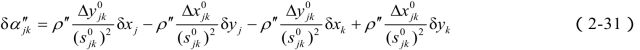
也可表示为
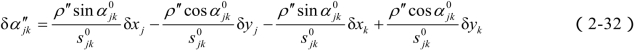
式（2-31）和式（2-32）即坐标改正数与坐标方位角改正数间的一般关系式，称坐标方位角改正数方程。坐标方位角改正数方程具有以下特点：
（1）当两个端点之一为已知点时，对应点的坐标改正数为零，而两个端点都是已知点时，两点间坐标方位角是已知值而无改正数方程。
（2）同一边正反坐标方位角改正数方程相等，因为：
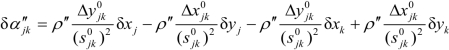
由于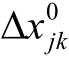
=-
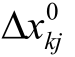和
=-
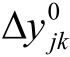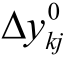，显然有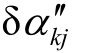
=δα′jk 。
对图2.2中角度观测值L，观测值平差值方程为
L+v=αjk-αjh
由于αjk=α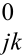
+δαjk，αjh=α
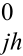+δαjh 就得到角度观测值误差方程：
将坐标方位角改正数方程（2-32）代入式（2-33），即得线性化后的角度观测值误差方程：
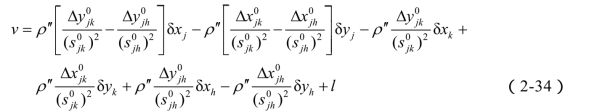
综上所述，角度观测值列误差方程的步骤可归纳为：
（1）计算各待定点近似坐标。
（2）按近似坐标计算近似坐标方位角和近似边长。
（3）列坐标方位角改正数方程，计算系数值。
（4）列角度观测值误差方程，求角度误差方程系数和常数项。
2.方向观测值的误差方程
（1）原始方向观测值误差方程。
测量平差程序设计时，通常不是以角度为观测值，而是以方向值作为观测值。其原因有两点：
①角度观测值并非误差独立，平差时近似作为独立观测值处理，理论上不够严密。(www.chuimin.cn)
②以方向值为观测值，程序设计处理起来更加方便。
如图2.3所示，测站点i观测j、k、h三个点，方向值分别是Lij，Lik，Lih ，设i测站零方向坐标方位角为Zi（定向角未知数），则观测值方程为
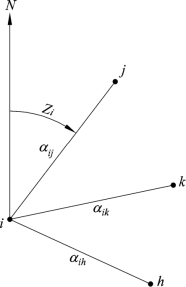
图2.3 方向观测值与坐标方位角
代入：
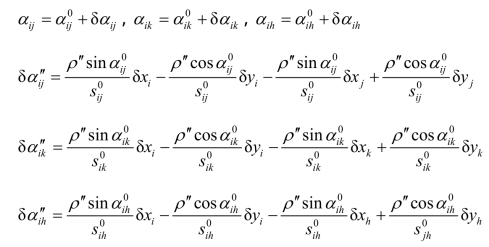
并令：
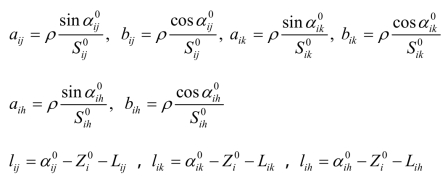
整理得方向观测值误差方程：
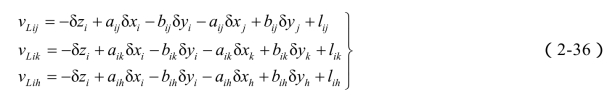
3.应用史莱伯法则后虚拟误差方程
以方向观测值组误差方程及法方程，由于每个测站增加了一个定向角未知数，未知数总数比以角度为观测值的未知数大约要增加50%。引入定向角未知数是建立数学模型的需要，平差关心是待定点坐标及其精度，定向角未知数本身没有什么意义。所以若能在组法方程前消除定向角未知数，对于降低法方程阶数是很有意义的。史莱伯法则就是从误差方程中消除定向角未知数，解出与原始误差方程同解的坐标未知数的方法。其具体操作步骤为：
（1）直接去掉方向值误差方程中的定向角未知数，得到虚拟的误差方程，如式（2-36）中方向观测值误差方程，去掉定向角未知数后为：
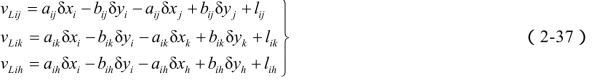
（2）将一个测站的虚拟的误差方程相加，得到一个新的虚拟的误差方程称为和方程。例如将式（2-37）3个虚拟误差方程相加得到如下和方程：
和方程的权定义为：p=-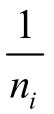
，其中ni是测站i的方向数。
（3）将虚拟误差方程（2-37）、（2-38）像误差方程（2-36）一样用于组法方程，则可从组成的法方程解算出与原始误差方程所组法方程同解的坐标未知数。
（4）间接平差计算[pvv]一般不采用公式[pvv]=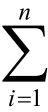
pivivi，而是采用下列计算公式计算：
采用史莱伯法则消去定向角未知数后，为使式（2-39）仍然成立，应使和方程常数项[l]i, [l]j ,4，等于0，为此要采用下式计算各测站定向角未知数近似值：
（5）若测站点和照准点均是已知点，则该方向误差方程应用史莱伯法则后消除，但是其常数项加入了和方程常数项[l]i。
4.观测边长误差方程
设边长观测值Li，两端点坐标平差值为xj,yj 和xk,yk ，相应的近似值和改正数为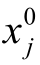
, y
, x
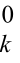,y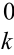
和δxj, δyj, δxk, δyk ，则观测值Li的观测值方程为
将式（2-41）在x
,y
,x
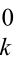,y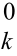
处展开为泰勒级数，并取至一次项得：
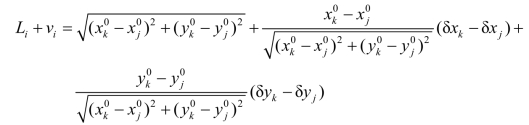
整理并令
即得线性化的边长误差方程：
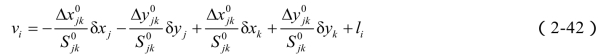
同样当端点j,k中有一个点为已知点时，则相应的坐标改正数δxj,δyj或者δxk,δyk为零。另外根据Δx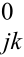
=-Δy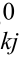
，可知边长误差方程与端点排序jk或kj无关。
有关测量平差程序设计 第2版的文章
- 详细阅读
-
如何检验平面度误差？详细阅读
平面度误差的检验一般有下面几种方法。然后将工件放在精密平板上，前后、左右平稳地移动几下，再取下工件仔细地观察摩擦痕迹分布情况，就可以确定工件平面度误差的大小。用透光法检验平面度误差 工件的平面度也可用样板平尺测量。若各处都不透光，表明工件平面度误差很小；若有个别段透光，则可凭操作者的经验，估计出平面度误差的大小。这种方法测量精度较高，而且可以得到平面度误差值，但测量时需要一定的技能。......
2023-06-28
- 详细阅读
- 详细阅读
-
平面控制网数据结构测量平差程序设计详细阅读
观测数据的录入按测站进行，首先录入测站名，每个测站名单独占一行，这也是平面控制网数据结构中唯一不带逗号分隔符的数据行。上述数据结构简单易记、无冗余信息。平差计算中需要的已知点数、待定点数、方向观测值数、边长观测值数、测站数、多余观测数等重要信息均反映在数据编排格式中，平差计算程序在录入数据时，可以自行判读或计算出来，因而极大地方便了用户，是测量平差程序数据结构设计的典范。......
2023-10-22
-
测量平差程序设计2版|平面控制网数据读入详细阅读
和高程控制网数据格式一样，示例程序平面控制网数据格式也是只有两种。随之出现的即是已知数据信息。已知数据信息的行数等于已知点数，随着控制网不同而异，但是测站信息就是其结束的标志。作为通用平差程序，要适用于导线网（边角网）、三角网、三边网及各种边角交会图形的混合控制网型，需要分别对lb（）、sb（）数组进行查询，找出未设过测站的控制点，将其点名加入点名数组dm（）。......
2023-10-22
-
刚体在平面的运动方程详细阅读
刚体上与平面Ⅱ相交的部分，称为“平面图形”，用S 表示。根据平面运动的特征，当刚体做平面运动时，平面图形S 上各点始终在平面Ⅱ运动。为研究平面图形S 在其自身平面内的运动，在此平面内建立静坐标系Oxy。式称为“刚体平面运动方程”。......
2023-06-19
-
测量平差程序设计：误差方程与法方程系数对应关详细阅读
所以为了节省内存，平差示例程序中采用一维数组保存法方程系数，并且只保存主对角线以上的数值，因而法方程系数阵称为上三角阵。例如pibidi中bi、di在误差方程系数数组中的下标分别是2、4，填充到法方程系数阵二维数组变量中的下标就是（2，4）。......
2023-10-22
相关推荐