基于上述定义的频率动态轨迹的特征指标,建立误差模型函数。依据所研究的频率动态问题,分别在每组确定的系统参数下,首先选取若干个有实际参考意义的频率实测轨迹;其次利用电力系统仿真软件仿真得到频率仿真轨迹;然后通过上述已建立的单功率脱落事件下的误差模型计算误差值,并对这些样本进行两两比较,形成判断矩阵;最后通过对判断矩阵进行求解,得到各个样本的权重系数。......
2023-06-29
1.确定未知数的个数
对于一个确定的平差问题,能并且只能设置t个函数独立的未知参数,所以确定未知数个数实际上就是确定必要观测数。根据确定一个未知数,需要一个独立观测值的原则,高程控制网必要观测数等于待定点个数;平面控制网在有足够起算数据的情况下,必要观测数为待定点数的2倍。作为特殊情况,平面控制网中有单独的起算边或起算坐标方位角(至少有一个端点是待定点的情况),则必要观测数还应减去单独起算边或起算坐标方位角数目。
2.未知参数的选择
为了确保每一个观测值平差值都能表示为待定参数的函数(观测值方程),待定参数必须足数并且函数独立。另外运用最小二乘准则求特解时,采用的是求自由极值原理,这也要求各待定参数间函数独立,即任意一个待定参数不可表示为其余参数的函数。
理论上参数选择在足数、函数独立的原则下是任意的,既可以选观测值平差值,也可以选观测值平差值的函数值。由于控制测量的目的就是确定待定点坐标或高程,因而在实际应用中,总是选择待定点坐标和高程值为未知参数。这样不仅可以直接获得平差最终值,也极大地方便了精度评定,同时未知参数一定是函数独立的。
3.误差方程建立
设观测值平差值为待点参数的线性函数,其函数一般形式为
代入 i=Li+vi,并令li=di-Li ,即得到误差方程为(www.chuimin.cn)
i=Li+vi,并令li=di-Li ,即得到误差方程为(www.chuimin.cn)
4.观测值方程的线性化
平面控制网观测值方程一般是非线性的,要建立线性化误差方程,必须将其线性化。线性化的方法是将其按泰勒级数展开,因此必须首先求得计算待定参数的近似值,在近似值处将观测值方程展开为泰勒级数取至一次项。
设有非线性观测值方程:
将待定参数表示为近似值加改正数xj=x +δx,代入公式(2-28)并按泰勒级数展开取至一次项得到:
+δx,代入公式(2-28)并按泰勒级数展开取至一次项得到:
当近似值x 给定后,各未知数近似值改正数δx前的系数可由近似值x
给定后,各未知数近似值改正数δx前的系数可由近似值x 代入
代入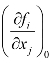 求得。若令
求得。若令 即得到公式(2-27)表示的线性误差方程形式。
即得到公式(2-27)表示的线性误差方程形式。
线性化是假定δxj的二次及二次以上项是小量而忽略不计,因此确定未知数近似值x 的基本要求是δxj足够小,即x
的基本要求是δxj足够小,即x 足够接近xj。若满足这一要求,则虽然未知数近似值会因推算路线不同而异,但平差结果是相同的。当不能满足这一条件时,会引起计算误差,必要时可选择迭代进行(将第一次平差后的平差值作为近似值,线性化列误差方程,再次平差)。
足够接近xj。若满足这一要求,则虽然未知数近似值会因推算路线不同而异,但平差结果是相同的。当不能满足这一条件时,会引起计算误差,必要时可选择迭代进行(将第一次平差后的平差值作为近似值,线性化列误差方程,再次平差)。
有关测量平差程序设计 第2版的文章

基于上述定义的频率动态轨迹的特征指标,建立误差模型函数。依据所研究的频率动态问题,分别在每组确定的系统参数下,首先选取若干个有实际参考意义的频率实测轨迹;其次利用电力系统仿真软件仿真得到频率仿真轨迹;然后通过上述已建立的单功率脱落事件下的误差模型计算误差值,并对这些样本进行两两比较,形成判断矩阵;最后通过对判断矩阵进行求解,得到各个样本的权重系数。......
2023-06-29

ADCP的测量精度主要受海况、水质、噪音及船速等几方面的影响。根据上述分析,可以采取以下措施控制船载式ADCP流量测验误差:①一般情况下,ADCP适用于河面宽、水深及流速大的河流;测验前需对ADCP进行定点比测,以确保ADCP性能稳定。高含沙量的影响程度与ADCP的系统频率有很大关系。因此,对高含沙量的河流,宜选用频率较低的ADCP系统。......
2023-11-29

平面一般力系平衡的充分与必要条件是:力系的主矢和主矩同时为零。上式称为平面一般力系的平衡方程,平面一般的平衡方程有三个,可求解最多三个未知量。显然各力作用线在同一平面内且任意分布,属于平面一般力系。列平衡方程要根据物体所受的力系类型列出。比如,平面任意力系只能列出三个独立的平衡方程,平面汇交力系或平面平行力系只能列两个;平面力偶系只能列一个;对于由n 个物体组成的系统,可列出3n 个。......
2023-06-19

所以为了节省内存,平差示例程序中采用一维数组保存法方程系数,并且只保存主对角线以上的数值,因而法方程系数阵称为上三角阵。例如pibidi中bi、di在误差方程系数数组中的下标分别是2、4,填充到法方程系数阵二维数组变量中的下标就是(2,4)。......
2023-10-22

式和式构成矢量控制基本方程式,定子电流解耦成ism和ist两个分量,ist为励磁电流分量,ψr为转子磁链。在这种情况下,常利用矢量控制方程中的转差公式,构成转差型的矢量控制系统,又称间接矢量控制系统。矢量控制的实质是将交流电动机等效为直流电动机,分别对速度和磁场两个分量进行独立控制。......
2023-06-19

前面介绍了利用位移法基本结构来建立位移法方程。位移法典型方程实质上代表了原结构的结点和截面的平衡条件。因此,位移法方程的建立可以不通过附加约束的基本结构,而是利用杆件的物理方程[式(7-1)至式(7-4)],直接取结点和截面一侧为隔离体的平衡条件,来建立以结点位移为未知量的位移法方程。利用等截面直杆的物理方程式(7-1)、式(7-2)及表 7-1,由跨度 l=12 m,高 h=6 m,可得图7-16建立位移法方程。......
2023-08-30

水深精度应理解为改正后水深的精度。在确定水深精度时,需对各误差源进行定量表示。由于水深测量的特点是测量深度数据缺少多余观测值,因而水深精度主要取决于对影响水深值的系统误差和可能的随机误差的估计精度。......
2023-11-29
相关推荐