如果说中误差是衡量精度的绝对指标，则权是衡量精度的相对指标。精度高于它的观测值，权大于1，反之则小于1，而精度与之相等的，则权必为1，所以m又称为单位权中误差。实际上m0并不限定要选择已有观测值的中误差，不论实际上有无对应的观测值，中误差为m0的观测值均称为单位权观测值，其在评定精度工作中的作用相同。......
2023-10-22
测量平差程序设计：精度数字指标
【摘要】：由于参数σ决定了误差分布的离散程度，因而可以采用σ作为衡量精度的数字指标，概率统计称之为标准差，测量上称为中误差。根据偶然误差的特性，显然有E(Δ)=0，所以测量学取为衡量精度的数值指标是不难理解的。精度数字指标只是误差数值的估算值，不等于确定的误差值，但是中误差相同的观测值，对应着相同的误差分布，被称为等精度观测值。
正态分布概率密度函数最大值为
，其值的大小与参数σ成反比。对于一个必然事件概率值为1，以图形解释即概率密度曲线与横轴围成的面积值为1，因而f（0）越大，概率密度曲线形状就越陡峭，反之则越平缓，而σ小则f（0）大，σ大则f（0）小，所以σ决定了曲线的形状（图2.1）。
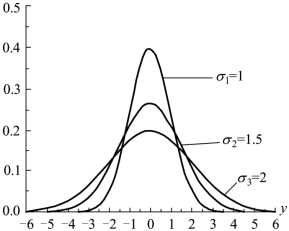
图2.1 正态分布曲线
对于形状陡峭的概率密度曲线，很显然随着误差绝对值的加大，概率值迅速地减小，即偶然误差更集中地分布在0附近，称为误差分布离散度小。反之形状平缓的概率密度曲线，则表明偶然误差分布较为分散，或者说离散度大。不难理解，离散度小时，偶然误差集中分布在0点附近，偶然误差绝对值小得多，说明观测值质量较好，或者说精度较高；反之，离散度较大时，表明偶然误差在0点附近的集中程度较低，因而对应的观测值质量较差，或者说精度较低。由此可见，精度又可以定义为误差分布的离散程度。
由于参数σ决定了误差分布的离散程度，因而可以采用σ作为衡量精度的数字指标，概率统计称之为标准差，测量上称为中误差。两个（组）观测值的中误差σ相同，则称两个（组）观测值为同精度观测值，反之则是不等精度观测值。标准差的平方2σ在概率统计中称为方差，理论上等于偶然误差平方的期望值，即(www.chuimin.cn)
可见，方差实际上是偶然误差平方的理论平均值，或者说是以概率值为权，无穷观测条件下的加权幂平均值。根据偶然误差的特性，显然有E(Δ)=0，所以测量学取
为衡量精度的数值指标是不难理解的。
精度数字指标只是误差数值的估算值，不等于确定的误差值，但是中误差相同的观测值，对应着相同的误差分布，被称为等精度观测值。等精度观测值不等于其真实误差相同，由于真误差不可知，因而测量上认为同样的观测条件，对应着同样的误差分布，而对应于同一误差分布的各观测值，都是等精度观测值。
实践中不可能得到真误差，也不可能有无限次的观测，因而式（2-2）只是一个无法实际应用的定义式。实践中是利用观测值改正数得到σ的估算值，测量学称σ的估算值为中误差，习惯上以字符m表示。
有关测量平差程序设计 第2版的文章
- 详细阅读
-
测量平差程序设计：精度评定与协因数传播详细阅读
对式应用协因数传播律：即法方程系数阵的逆阵，就是未知参数的协因数阵。平面控制网除了评定待定点坐标中误差外，还常常需要评定坐标方位角和边长平差值的精度，这就需要将其表示为未知参数的函数，并应用协因数传播律求评定值权倒数。根据协方差或协因数传播律知，函数值F精度与常数项φ无关。将非常数项表示为：式实际上就是函数F的全微分，将其称为权函数式，矩阵式为：对权函数式应用协因数传播律，求得权倒数：......
2023-10-22
-
测量平差的基本概念-《测量平差程序设计第2版详细阅读
条件方程有两种形式：①直接表示观测值平差值应满足的条件，其一般形式为f()=0，其中表示观测值向量的平差值。②设定一组数目为t的函数独立参数，将所有观测值平差值表示为的函数，其一般形式为=fi()。测量平差中将观测值代入后所得不符值称为闭合差。......
2023-10-22
-
测量平差程序设计：对象概念详细阅读
图1.7属性栏②通过程序代码赋值。图1.8访问Label1.Caption属性运行结果访问对象的方法。方法是VB为对象预设的、用户不能更改的事件过程，不同的对象具有不同的方法。前者由滚动条的Value值变化激发，后者在滚动框被拖动时引发。......
2023-10-22
-
测量平差程序设计方程法详细阅读
设有n个观测值，组成误差方程组为：应用最小二乘准则组成法方程组，其纯量形式为：其中法方程系数、常数阵中的数值由此可见自乘系数[paa]是由n个值的和组成，这n个值分别是各观测值误差方程中第一个未知数系数平方乘以观测值的权；互乘系数[pab]也是由n个值的和组成，这n个值分别是各观测值误差方程中第一个和第二个未知数系数之积乘以观测值的权。根据这一特点，平差程序组法方程采用的算法是：①按测站循环。......
2023-10-22
-
测量平差程序设计：工程概念详细阅读
Visual Basic 6.0可以创建标准的Windows应用程序、ActveX与Active文档等，在设计阶段，VB通称它们为一个工程。设计VB程序涉及工程与文件的新建、保存、移除等多种操作，这些操作贯穿于创建应用程序的整个过程。工程资源管理器是用来管理工程的，它的功能就像Windows中的资源管理器一样。图1.21工程资源管理器在工程资源管理器中，显示有工程名、工程文件名、窗体名和窗体文件名。工程名为VB对用户所创建的应用程序的标识。......
2023-10-22
-
测量平差程序设计：过程的定义详细阅读
VB程序是由过程组成的，每个过程是为了完成设定的任务，由一组独立的程序代码组成。图1.11添加过程对话框在“添加过程”对话窗口中只需确定过程名称、类型等信息后回车确定，VB系统即可自动生成“过程”的首尾关键字，用户所需做的工作只是在其中编写代码。......
2023-10-22
-
测量平差程序设计：模块和层次结构详细阅读
图1.1VB应用程序的组织结构1.窗体模块窗体模块包含窗体及其控件的属性设置、事件过程、窗体内自定义过程的窗体级声明等。标准模块是VB程序中的一个独立模块，包含模块级或全局变量声明、函数过程和通用过程，标准模块的文件扩展名为.bas。标准模块中除包含允许其它模块访问的过程，还包括变量、常量、数据类型、自定义过程的全局或模块级声明。......
2023-10-22
相关推荐