直线运动数值表示位移规律及刹车问题分析

2023-10-21 理论教育版权反馈

【摘要】：当物体做直线运动时,可用带有正负号的数值表示位移,取正值时表示其方向与规定正方向一致,反之则相反。 -2 45 本题考查匀变速直线运动规律中的刹车问题。

1.误差。(B)

2.有效数字。(B)

3.参考系。(B)

4.质点。(B)

5.路程和位移。(B)

6.时间和时刻。(B)

7.平均速度和瞬时速度。(B)

8.加速度。(C)

9.匀变速直线运动。(D)

10.匀变速直线运动的速度图像。(C)

11.自由落体速度。(C)

12.重力加速度。(C)

近三年四川省对口升学本章考点内容及考题分析

本章为运动学基础,是本部分的基础内容,重点掌握误差和错误的区别,路程和位移的区别与联系,时间和时刻的区别与联系,平均速度和瞬时速度的区别与联系,加速度,匀变速直线运动的规律,自由落体运动;理解在v0,vt,a,t,s五个物理量中,已知三个物理量,求解另外两个物理量;掌握运动学常见的几个公式,会理解题意,抽象出物理问题,运用公式求解;会求平均速度,会用自由落体运动公式解题,理解自由落体的结论。

1.参考系的选择是任意的,一般选择地面或者地面上固定的物体作为参考系,研究对象与参考系位置关系发生改变的,研究对象就是运动的,位置关系不变则为静止。选择不同的参考系判断物体是运动的还是静止的,所得结果不同,叫作运动的相对性。

2.匀速直线运动:物体沿一直线运动,任意相等的时间内通过的位移都相等。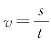是比值定义法,不能说速度与位移成正比,与时间成反比。

3.平均速度与瞬时速度

(1)平均速度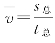,注意计算平均速度要用总位移除以总时间。前一半路程的平均速度为v1,后一半路程的平均速度为v2,则全程的平均速度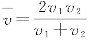。前一半时间的平均速度为v1,后一半时间的平均速度为v2,则全程的平均速度。切记平均速度不是速度的代数平均值。

(2)瞬时速度是指运动物体在某一时刻或某一位置时的速度,简称速度。

4.时刻和时间

(1)时刻指的是某一瞬时,是时间轴上的一点,对应于位置、瞬时速度、动量、动能等状态量,通常说的“2秒末”“速度达2 m/s时”都是指时刻。

(2)时间是两时刻的间隔,是时间轴上的一段。对应位移、路程、冲量、功等过程量。通常说的“几秒内”“第几秒内”均是指时间。

5.位移和路程

(1)位移表示质点在空间的位置的变化,是矢量。位移用有向线段表示,位移的大小等于有向线段的长度,位移的方向由初位置指向末位置。当物体做直线运动时,可用带有正负号的数值表示位移,取正值时表示其方向与规定正方向一致,反之则相反。

(2)路程是质点在空间运动轨迹的长度,是标量。在确定的两位置间,物体的路程不是唯一的,它与质点的具体运动过程有关。

注意:质点就是有质量但不存在体积或形状的点,是物理学的一个理想化模型。在物体的大小和形状不起作用,或者所起的作用并不显著而可以忽略不计时,我们近似地把该物体看作是一个只具有质量而其体积、形状可以忽略不计的理想物体,用来代替物体的有质量的点称为质点。

6.加速度

(1)加速度是描述速度变化快慢的物理量。

(2)速度的变化量与所需时间的比值叫加速度。

(3)公式:,单位:m/s2是速度的变化率。

(4)加速度是矢量,其方向与Δv的方向相同。

(5)注意v,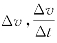的区别和联系。Δv大,而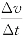不一定大,反之亦然。(注意判断题)

7.匀变速直线运动是指物体沿直线运动,在任意相等的时间内,速度的变化都相等的运动。常用的匀变速运动的公式有

(1)说明:上述各式有v0,vt,a,s,t五个量,其中每式均含四个量,即缺少一个量,在应用中可根据已知量和待求量选择合适的公式求解,能够熟练计算已知其中三个量求另外两个量,⑤式中T表示连续相等时间的时间间隔。

(2)上述各量中除t外其余均为矢量,在运用时一般取v0的方向为正方向,若该量与v0的方向相同则取为正值,反之为负值。对已知量代入公式时要带上正负号,对未知量一般假设为正,若结果是正值,则表示与v0方向相同,反之则表示与v0方向相反。另外,在规定v0方向为正的前提下,若a为正值,表示物体做加速运动,若a为负值,则表示物体做减速运动;若v为正值,表示物体沿正方向运动,若v为负值,表示物体沿反方向运动;若s为正值,表示物体位于出发点的前方,若s为负值,表示物体位于出发点的后方。

(3)注意:以上各式仅适用于匀变速直线运动,包括有往返的情况,对匀变速曲线运动和变加速运动均不成立。

8.图像

能够运用图像解题,做题中学生要尽量抽象出物理模型和图像,识记匀速直线运动和匀变速直线运动的s-t图、v-t图,在图中理解初速度为零的匀加速直线运动的两个重要比值:相等时间内的位移比1∶3∶5;相等位移上的时间比1∶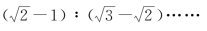

9.自由落体运动

初速为0,加速度为g的匀加速运动,位移公式:;速度公式:vt=gt。相当于已知初速度和加速度,只需要再知道一个物理量就可以求其余两个物理量。

10.要熟悉刹车问题,追击问题,相遇问题的题型。

【例1】以速度为10 m/s匀速运动的汽车在第2 s末关闭发动机,以后为匀减速运动,第3 s内平均速度是9 m/s,则汽车加速度是_________m/s2,汽车在10 s内的位移是_________m。

【答案】 -2 45

【解析】本题考查匀变速直线运动规律中的刹车问题。求解刹车问题时,一定要判断清楚汽车实际运动的时间。

解:第3 s初的速度v0=10 m/s,第3.5 s末的瞬时速度vt=9 m/s(第3 s内的平均速度就为第3.5 s末的瞬时速度)所以汽车的加速度:

“-”表示a的方向与运动方向相反。

汽车关闭发动机后速度减到零所经时间:

则关闭发动机后汽车8 s内的位移:

前2 s汽车匀速运动:

s1=v0t1=10×2=20(m)

汽车10 s内总位移:

s=s1+s2=20+25=45(m)

说明:(1)求解刹车问题时,一定要判断清楚汽车实际运动的时间。

(2)本题求s2时也可用公式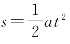计算,也就是说“末速度为零的匀减速运动”可倒过来看作“初速度为零的匀加速运动”。

【例2】 (2018年高考题)货车从车站出发,以v=8 m/s的速度匀速直线行驶,经过2.5 s后,汽车从同一车站出发,以加速度a=2 m/s2做匀加速直线运动去追赶货车。求:

(1)汽车追上货车所需要的时间;(www.chuimin.cn)

(2)汽车追上货车之前两车间的最大距离。

【答案】 (1)设汽车追上货车的时间为t1。t1=10 s(-2 s不符合题意舍去)所以汽车追上货车的时间为10 s;(2)当汽车速度达到v=8 m/s时,两车距离相差最大,所用时间为t2。

所以汽车追上货车之前两车间的最大距离为36 m。

【解析】本题考查匀变速直线运动规律中的追击问题。

【例3】在铁轨上有甲、乙两列列车,甲车在前,乙车在后,分别以速度v1=15 m/s,v2=40 m/s做同向匀速运动。当甲、乙间距为1500 m时,乙车开始刹车做匀减速运动,加速度大小为0.2 m/s2,问:乙车能否追上甲车?

【答案】由于乙车速度大于甲车的速度,因此尽管乙车刹车后做匀减速直线运动,速度开始减小,但其初始阶段速度还是比甲车的大,两车的距离还是在减小,当乙车的速度减为和甲车的速度相等时,乙车的位移大于甲车相对乙车初始位置的位移,则乙车就一定能追上甲车。设乙车速度减为v1=15 m/s时,用的时间为t,则有

在这段时间里乙车的位移:

在该时间内甲车相对乙车初始位置的位移:

s1=1500+v1t=1500+15×125=3375(m)

因为s2＞s1,所以乙车能追上甲车。

【解析】本题考查匀变速直线运动规律中的追击问题。

【例4】建筑工人安装塔手架进行高空作业,有一名建筑工人由于不慎将抓在手中的一根长5 m的铁杆在竖直状态下脱落了,使其做自由落体运动,铁杆在下落过程中经过某一楼层面的时间为0.2 s,试求铁杆下落时其下端到该楼层的高度?(g=10 m/s2,不计楼层面的厚度)

【答案】铁杆下落做自由落体运动,其运动经过下面某一楼层时间Δt=0.2s,这个Δt也就是杆的上端到达该楼层下落时间tA与杆的下端到达该楼层下落时间tB之差,设所求高度为h,则由自由落体公式可得

解得h=28.8 m,

所以铁杆下落时其下端到该楼层的高度为28.8 m。

【解析】本题考查自由落体运动。

一、单项选择题

1.关于加速度,下列说法错误的是( )

A.加速度反映了速度变化的大小

B.速度很大的物体,加速度可能很小,加速度为零时,速度不一定为零

C.加速度很大的物体,速度可能很小,速度为零时,加速度不一定为零

D.物体的速度有变化,则一定有加速度

2.一质点向北做匀变速直线运动,其位移表达式为s=(8t-2t 2)m,则( )

A.质点做匀加速直线运动 B.质点的加速度大小是4 m/s2

C.质点的加速度大小是2 m/s2 D.在第10 s末速度大小是5 m/s

3.一物体从静止开始做匀加速直线运动,当位移为s时,速度为v,接着物体以v为初速度又做匀加速直线运动,又运动了位移s后,速度为2v。在整个过程中,物体的平均速度为( )

4.一物体做匀加速直线运动,从某一时刻起,连续2 s内通过的路程分别为1.2 m和3.2 m,则计时开始的速度为( )

A.1 m/s B.2 m/s C.0.1 m/s D.0.2 m/s

5.屋檐上每隔相等时间积成一滴水落下,当第一滴水落地时,第5滴水刚好开始下落,观察到第4、5滴水之间此时距离为1 m。若g取10 m/s2,则屋檐高度为( )

A.4 m B.7 m C.16 m D.5 m

二、判断题(正确的选“A”,错误的选“B”)

1.同一运动选择不同的参考系,观察结果可能会有所不同。( )

2.由于仪器结构上的不完整产生的误差属于系统误差。( )

3.若测量结果为1.30,则有效数字为三位。( )

4.物理实验中的误差是可以避免的。( )

5.自由落体运动,在开始连续的三个1 s内通过的位移之比为1∶3∶5。( )

三、填空题

1.汽车在从甲地开往乙地过程中:若前一半路程的平均速度是40 km/h,后一半路程的平均速度是60 km/h,则全程的平均速度是_________km/h。

2.汽车在从甲地开往乙地过程中若前一半时间的平均速度是40 km/h,后一半时间的平均速度是60 km/h,则全程的平均速度是_________km/h。

3.甲、乙两个质量之比为1∶3的物体从同一高度自由落下,当落下相同高度时,它们的动能之比为_________。

4.一物体由静止开始做匀加速直线运动,在前4 s内位移64 m,则物体经过前一半位移所需的时间是_________s;物体在前一半时间内通过的位移是_________m。

5.某辆汽车刹车时能产生的最大加速度为10 m/s2,司机发现前方有危险时要经0.7 s(反应时间)才能做出反应马上制动。若汽车以20 m/s的速度行驶,从开始刹车到停车的距离是________m。

四、分析计算题

1.一辆做匀速直线运动的汽车,在5 s内通过相距50 m的两电线杆A、B,汽车经过B杆后改做匀加速直线运动到达另一电线杆C时速度达到15 m/s。若B、C两电线杆也相距50 m,则汽车的加速度是多少?

2.将一物体以12 m/s的速度竖直上抛,经过1 s后物体的速度变为0,然后以自由落体运动下落。假定运动中空气阻力f大小不变,试求物体落回原位置时的速度。(g取10 m/s2)

3.物体A和B在同一直线上运动,A在某时刻的速度为2 m/s,以0.2 m/s2的加速度做匀减速前进,2 s后与原来静止的B发生碰撞,碰撞后A以碰撞前的速率的一半反向弹回,仍做匀减速运动,加速度的值不变,B获得与碰撞后的A相同的速率,以0.4 m/s2的加速度做匀减速运动。不计碰撞所用的时间,求:

(1)B停止时所用的时间;

(2)B停止时所经过的位移。

4.某物体由静止开始以2 m/s2的加速度运动10 s后,匀速运动2 min,然后在20 s内做匀减速运动直到停止。求:

(1)物体运动的位移;

(2)物体运动过程中的平均速度。

5.一辆汽车正以10 m/s的速度前进,由于突发事件,驾驶员紧急刹车,若要求汽车在5 s内停下,试求:

(1)汽车允许滑行的最大距离是多少?

(2)刹车的加速度最小为多大?

直线运动数值表示位移规律及刹车问题分析

相关推荐