四川省对口升学最新考点及考题分析，解析复杂直流电路及电源模型

1.支路、节点、回路的概念。(C)

2.基尔霍夫电流定律和电压定律。(C)

3.支路电流法分析具有3条支路的直流电路。(D)

4.二端网络与有源二端网络。(A)

5.戴维宁定理分析两个网孔直流电路的步骤。(B)

6.两种实际电源模型之间的等效变换。(B)

近三年四川省对口升学本章考点内容及考题分析

本章复习的重点是应用支路电流法分析求解具有3支路的复杂直流电路;应用戴维宁定理分析和计算两网孔复杂直流电路;会对电压源和电流源两种电源模型进行等效互换。本章复习的难点是戴维宁定理的理解和应用。

本章复习时要注重分析计算题的训练,注意计算题的书写要求,要有必要的文字说明,体现出解题的物理思想、列写原始方程、作图要规范等。

一、支路与节点、回路与网孔

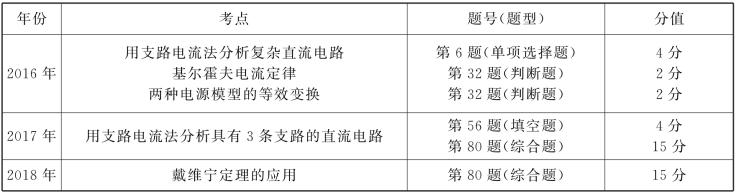
1.支路:由一个或多个元件组成的无分支的一段电路。如图1-3-1所示的电路中有3条支路。

2.节点:由三条或三条以上的支路组成的连接点。图1-3-1电路中A、B为节点。

3.回路:电路中的任一闭合路径。图1-3-1所示的电路中,有3个回路。

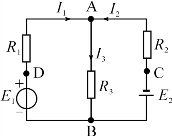
图1-3-1

4.网孔:闭合电路内不含其他支路的回路,称为网孔。因此,网孔是回路的一种,是一种较简单的回路。图1-3-1中有2个网孔,如图中的回路ABDA、ABCA称为网孔。

二、基尔霍夫电流定律与基尔霍夫电压定律

1.基尔霍夫电流定律(KCL)

基尔霍夫电流定律于1845年由德国物理学家古斯塔夫·基尔霍夫发现。该定律又称节点电流定律,其内容是在电路中任一节点上,在任一时刻,流入节点的电流之和等于流出节点的电流之和。换句话说,所有流进的电流必须全部流出。即

∑I入=∑I出

假设流入某节点的电流为正值,流出该节点的电流为负值,则所有涉及这一节点的电流的代数和等于零。即

∑I=0

基尔霍夫电流定律可以推广应用于电路的任一假想闭合面。

2.基尔霍夫电压定律(KVL)

基尔霍夫电压定律又称为回路电压定律。其内容是在任何一个闭合回路中,各段电阻上的电压降的代数和等于电动势的代数和,即

∑IR=∑E

从一点出发绕回路一周回到该点时,各段电压的代数和恒等于零,即

∑U=0

基尔霍夫电压定律不仅可以用在任一闭合回路,还可以推广到任一不闭合的电路上,但要将开口处的电压列入方程。

凡电压的参考方向与回路绕行方向一致者,在该电压取“+”号,反之,为“-”号。

【例】 图1-3-1中可列出基尔霍夫电流定律方程为

I1+I2=I3

I1+I2-I3=0

或列出基尔霍夫电压定律方程为

I1R1+I3R3-E1=0

I2R2+I3R3-E2=0

I1R1+UAB-E1=0

三、支路电流法的应用

1.支路电流法

支路电流法以支路电流为未知量,依据基尔霍夫定律和欧姆定律列出节点电流方程和回路电压方程,然后联立方程求出各支路电流。

2.用支路电流法计算电路的具体步骤

(1)假设各支路电流。在电路图中标出各支路的电流的参考方向。

(2)列写KCL方程。一般来说,对具有n个节点的电路运用基尔霍夫电流定律只能得到(n-1)个独立的KCL方程。

(3)列写独立的KVL方程。独立的KVL方程数为单孔回路的数目(即网孔数)。

(4)联立所有列写的方程,即可求解出各支路电流,进而求解电路中电压、功率等。

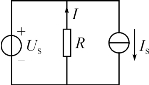
【例】 (2014年高考题)电路如图1-3-2所示,已知US=10 V,IS=2 A,R1=1Ω,R2=2Ω,R3=1Ω。用支路电流法求:

图1-3-2

(1)各支路电流;

(2)电流源两端电压U;

(3)电路中各电阻所消耗的功率。

【解析】

(1)由基尔霍夫定律得

I1+I2-I3=0(I2=IS=2 A)

I1R1+I3R3-US=0

联立解得,I1=4 A,I2=2 A,I3=6 A

(2)由基尔霍夫定律得

I2R2+I3R3-U=0

则U=I2R2+I3R3=2×2+1×6=10(V)

(3)电阻R1、R2、R3上所消耗的功率分别为

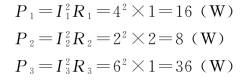
四、回路电流法的应用

1.回路电流法

回路电流法:以回路电流为未知量,根据KVL列出独立回路的电压方程,然后联立求解的方法。

(1)主要针对支路比较多的电路。

(2)和支路电流法相比,列出的方程明显减少,利于计算。

(3)多个回路电流流过的电阻,在每个回路方程中要得到体现,这就是回路电流法的注意点。

2.回路法解题的一般步骤

(1)选定K=b-(n-1)个独立回路,并确定其绕行方向;

(2)对K个独立回路,以回路电流为未知量,列写其方程;

(3)求解上述方程,得到K个回路电流;

(4)求各支路电流;

(5)其他分析。

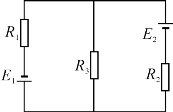
图1-3-3

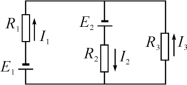
【例】 电路如图1-3-3所示,已知电源电动势E1=6 V,E2=1 V,电源内阻不计,电阻R1=1Ω,R2=2Ω,R3=3Ω。求各支路上的电流。

【解析】

假设回路电流如图1-3-4所示。

由基尔霍夫电压定律得

I11(R1+R3)+I22R3+E1=0

I22(R2+R3)+I11R3-E2=0

联立方程组解得I11=-3 A,I22=2 A

故R1上电流大小为I1=-I11=3 A,方向向下。

R2上电流大小为I2=I22=2 A,方向向上。

R3上电流大小为I3=-(I11+I22)=-(-3+2)=1(A),方向向上。

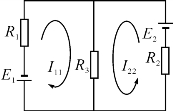
图1-3-4

注意:R3支路在两个网孔电压方程中都要有一个叠加电压。回路电流法一般用来求解支路多,回路也多,但网孔数少(不大于3个)的复杂直流电路。

五、叠加定理的应用

叠加定理是分析线性电路的一种重要方法,内容是在线性电路中,任一支路的电流(或电压),都是电路中各个电源分别独立作用下,在该支路中产生的电流(或电压)的代数和。

对于无源元件来讲,如果它的参数不随其端电压或通过的电流而变化,则称这种元件为线性元件。比如电阻,如果服从欧姆定律U=IR,则为常数,这种电阻就称线性电阻。由线性元件所组成的电路称为线性电路。

应用叠加定理解题的一般步骤如下。

(1)分别画出某一电源单独作用而其余电源不作用(但电源内阻要保留)时的分图,电路其余部分的联接以及电路中所有的电阻都不能变动;不作用的理想电压源用短路替代,理想电流源用开路替代。

(2)按简单直流电路的计算方法,利用电阻串、并联关系、欧姆定律等分别计算出各电源单独作用下各支路的电流(或电压)的大小和方向。

(3)将各支路的电流(或电压)叠加,也就是求出各电源在各支路产生电流(或电压)的代数和,这些电流就是各电源共同作用时在各支路产生的电流(或电压)。在求和时要注意各个电流(或电压)的正负。

注意:叠加定理只能用于计算线性电路(即电路中的元件均为线性元件)的支路电流或电压,不能直接进行功率的叠加计算。

【例】 在图1-3-5所示的电路中,已知电源电动势E1=125 V,E2=120 V,电源内阻不计,电阻R1=40Ω,R2=36Ω,R3=R4=60Ω。用叠加定理求各支路的电流。

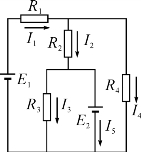
1-3-5

1-3-6

【解析】

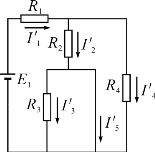
设E1单独作用时,E2用短路替代,电路如图1-3-6所示。

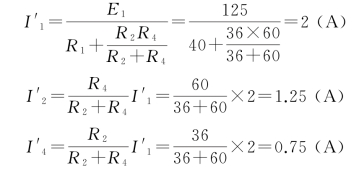
由于R3被短路,所以

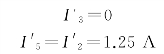
1-3-7

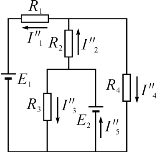
当E2单独作用时,E1用短路替代,电路如图1-3-7所示。

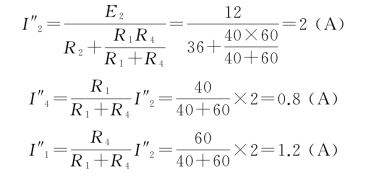
因为电动势E2直接加在R3两端,故电流

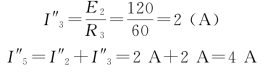
将各电源单独作用时所得支路电流叠加,有

I1=I′1-I″1=2-1.2=0.8(A)(实际电流方向与所标参考方向相同)

I2=I′2-I″2=1.25-2=-0.75(A)(实际电流方向与所标参考方向相反)

I3=I′3+I″3=0+2=2(A)(实际电流方向与所标参考方向相同)

I4=I′4+I″4=0.75+0.8=1.55(A)(实际电流方向与所标参考方向相同)

I5=I′5-I″5=1.25-4=-2.75(A)(实际电流方向与所标参考方向相反)

六、戴维宁定理的应用

1.二端网络

(1)二端网络的定义:任何具有两个引出端的电路(网络)都可称为二端网络。

(2)无源二端网络:不含电源的二端网络称为无源二端网络,如电阻器的串联、并联和混联电路都属于无源二端网络,它们都可以等效成一个电阻器。

(3)有源二端网络:含有电源的二端网络称为有源二端网络。对外电路来说,任意一个有源二端线性网络都可以用一个电压源来等效替代,该电压源的电动势等于二端网络的开路电压,其内阻等于有源二端网络内所有电源不作用(电压源视为短路,电流源视为开路)仅保留内阻时网络两端的等效电阻,这就是戴维宁定理。

2.应用戴维宁定理解题的一般步骤

(1)把电路分为待求支路和有源二端网络两部分;

(2)移开待求支路,求出有源二端网络的开路电压;

(3)将有源二端网络内各电源除去,仅保留电源内阻,求出网络两端的等效电阻;

(4)画出等效电源接上待求支路,求出待求支路中的电流。

提示:一个复杂电路,并不需要把所有支路电流都求出来,而只要求出某一支路的电流,在这种情况下,应用戴维宁定理比较方便。

3.注意事项

(1)利用戴维宁定理等效只适用于线性有源二端网络。在利用定理分析电路时若待求支路为非线性,而二端网络为线性,则仍能使用该定理。

(2)该定理只对外电路等效,对二端网络内部不等效。也就是说,不可应用该定理求出等效电源电动势和内阻之后,又返回来求原电路(即有源二端网络内部电路)的电流和功率等。

(3)作等效电源时,要使电源电压的极性和有源二端网络开路电压的极性保持一致。

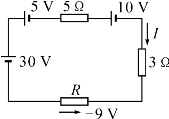
【例】 (2015年高考题)电路如图1-3-8所示,试用戴维宁定理求图中电流I。

图1-3-8

【解析】 移开待求支路,剩下的有源二端网络如图1-3-9(a)所示。该有源二端网络的开路电压为

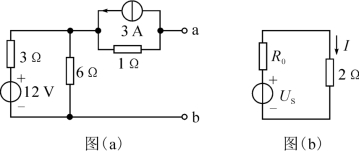
图1-3-9

该有源二端网络的等效电阻为

Rab=3∥6+1=3(Ω)

将有源二端网络等效成电压源并接入待求支路如图1-3-9(b)所示。

这里,US=Uab=5 V,R0=Rab=3Ω

则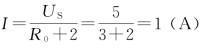

注意:该题中等效电压源的电压US的极性一定要与有源二端网络开路时的端电压Uab极性一致。

七、电压源与电流源的等效变换法的应用

1.电压源和电流源等效变换的含义

电压源与电流源互相变换后对同一负载供电性能不变(它们提供给负载的电压一样、电流大小相等、方向相同)称为这两个电压源和电流源的等效变换。

2.电压源和电流源等效变换的条件(如图1-3-10所示)

图1-3-10

(1)电流源的恒定电流等于电压源的短路电流。

(2)电压源和电流源的内阻相等。

(3)电压源的电动势US的方向与电流源恒定电流IS的方向必须保持一致。

(4)等效指的是外部等效,内部并不等效。因理想电压源内阻为R0=0,而理想电流源内阻RS为无穷大,不能满足R0=RS,故理想电压源与理想电流源不能等效变换。

(5)分析电路时可不考虑与理想电压源并联的电路元件,可视为开路;与理想电流源串联的电路元件可视为短路。

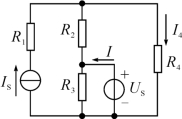
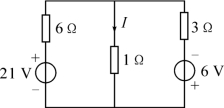
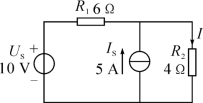
【例1】 (2018年高考题)如图所示的电路中,已知US=12 V,IS=4 A,R1=R2=R3=2Ω,R4=3Ω。

(1)用戴维宁定理求流过电阻R4的电流I4。

(2)求流过电压源US的电流I。

(3)求电流源IS的功率P。(www.chuimin.cn)

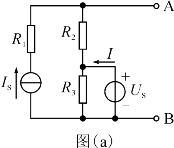
【答案】 (1)4 A (2)6 A (3)80 W

【解析】 (1)将R4支路断开,剩下的含源二端网络如图(a)所示,该含源二端网络的开路电压为

UAB=IS R2+US=4×2+12=20(V)

该网络的等效电阻为

RAB=R2=2Ω

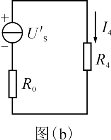
将该含源二端网络等效成电压源并接入待求R4支路,如图(b)所示,这里

U′S=UAB=20 V,R0=RAB=2Ω

则流过R4的电流为

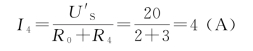
(2)由题可求出R3上的电流为

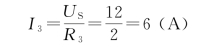
由基尔霍夫电流定律得

I3+I4-IS-I=0

解得,I=6 A

(3)设电流源IS两端电压为UIS,由基尔霍夫电压定律得

UIS=IS R1+I4R4=4×2+4×3=20(V)

则电流源的功率为

P=UIS IS=20×4=80(W)

【例2】 (2017年高考题)如图所示的直流电路已达到稳定,已知恒流源IS=3 A,恒压源U1=-1 V,恒压源U2=2 V,R1=3Ω,R2=1 Ω,R3=5Ω,L=100 m H,电感L的电阻忽略不计。试用支路电流法计算:

(1)各支路电流I1、I2和I3;

(2)IS的电压US及功率PS;

(3)恒压源U1和U2的功率。

【答案】 (1)I1=2 A I2=3 A I3=1 A

(2)6 V 18 W

(3)PU1=-2 W PU2=6 W

【解析】 (1)由题意可知

I2=IS=3 A ①

由基尔霍夫定律得

I1+I3-I2=0 ②

I1R1+U1-I3R3=0 ③

联立①②③解得

I1=2 A,I2=3 A,I3=1 A

(2)由基尔霍夫电压定律得

US-I3R3-I2R2+U2=0,解得US=6 V

电压、电流方向取非关联参考方向,则

PS=US·IS=6×3=18(W)

(3)恒压源U1的U2功率分别为

PU1=U1 I1=-1×2=-2(W)

PU2=U2I2=2×3=6(W)

恒压源U1的功率PU1＜0是负载,恒压源U2的功率PU2＞0是电源。

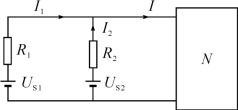
【例3】 如图所示的电路中,已知US1=100 V,US2=80 V,R2=2Ω,I=4 A,I2=2 A。试用基尔霍夫定律求电阻R1和负载N消耗的功率。

【答案】 12Ω 304 W

【解析】 由基尔霍夫定律得

I1+I2=I ①

I1R1-I2R2+US2-US1=0 ②

联立①②解得R1=12Ω

负载N消耗的功率为

P=(US2-I2R2)I=(80-2×2)×4=304(W)

【例4】 如图所示的电路中,已知US1=18 V,US2=8 V,IS=1 A,R=5Ω。求电路中各元件上的功率,指出哪些元件是电源,哪些是负载。并验证功率平衡关系。

【答案】 见解析。

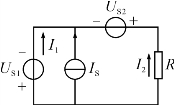
图(a)

【解析】 设支路电流为I1、I2如图(a)所示,由基尔霍夫定律得

I1+I2+IS=0 ①

US1-US2-I2R=0 ②

联立①②解得I1=-3 A,I2=2 A

电压、电流取关联参考方向,则

US1的功率为

PUS1=I1·US1=-3×18=-54(W),故US1是电源。

US2的功率为

PUS2·I2=16 W,故US2是负载。

IS的功率为

P1S=US1·IS=18×1=18(W),故IS是负载。

R是负载,消耗的功率为

PR=I 22R=22×5=20(W)

US1是电源,发出功率54 W,US2、IS、R均为负载,总吸收功率为54 W,功率平衡。

注意:

对于一个电路元件,当它的电压和电流的参考方向选为一致时,通常称为关联参考方向,在关联参考方向情况下,若元件功率P=UI为正值,表明该元件消耗功率,是负载;相反,若元件功率P=UI为负值,表明该元件发出功率,是电源。当一个电路元件的电压和电流的参考方向选为相反时,通常称为非关联参考方向,在非关联参考方向情况下,上述结论恰好相反,即当元件功率P=UI为正值时,表明该元件发出功率,是电源;当元件功率P=UI为负值时,表明该元件消耗功率,是负载。

【例5】 求如图所示电路中的电流I。

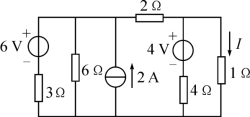
【答案】 2 A

【解析】 将题干图等效变换成图(a):

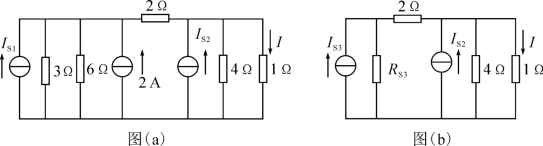
将图(a)等效变换成图(b):

IS3=IS1+2=4(A),RS3=3∥6=2(Ω)。

将图(b)等效变换成图(c):

这里US=IS3·RS3=4×2=8(V)。

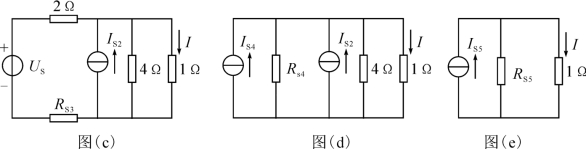
将图(c)等效变换成图(d):

RS4=2+RS3=2+2=4(Ω),。

将图(d)等效变换成图(e):

IS5=IS2+IS4=1+2=3(A),RS5=RS4∥4=4∥4=2(Ω),则×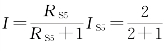3=2(A)。

注意:解题时一定要特别注意IS1与6 V电压源、IS2与4 V电压源的极性必须一致。

一、单项选择题

1.只有在电路中的________确定之后,电流才有正负之分。( )

A.各支路电流的实际方向 B.各支路电流的正方向

C.各支路电流的负方向 D.各支路电流的参考方向

2.如图所示的电路为某一电路中的一个节点,则I4为( )

A.0 B.5 A

C.10 A D.20 A

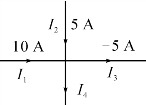
第2题图

第3题图

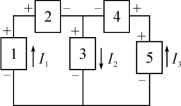
3.如图所示,5个方框分别代表电源和电阻器,其电压极性和电流方向如图所示,则代表电源的方框是( )

A.1和3 B.3和5 C.1和5 D.2和4

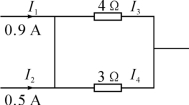
4.如图所示,I3为( )

A.1.4 A B.1 A C.0.8 A D.0.6 A

第4题图

第5题图

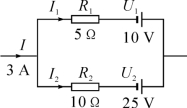
5.如图所示,I1和I2分别是( )

A.1 A,2 A B.2 A,1 A

C.3 A,0 D.0,3 A

6.戴维宁定理适用于对________进行等效计算,其所得电源只对________等效。( )

A.线性有源二端网络 外电路

B.非线性有源二端网络 内电路

C.线性有源二端网络 内电路

D.非线性有源二端网络 外电路

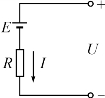
第7题图

7.如图所示,图中电流、电压、电动势三者之间的关系为( )

A.U=E-IR B.U=-E+IR

C.E=-U-IR D.E=U-IR( )

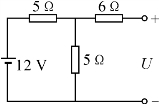
第8题图

8.如图所示,二端网络等效电路的参数为

A.8 V,7Ω

B.12 V,16Ω

C.10 V,2Ω

D.6 V,8.5Ω

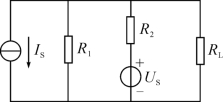
第9题图

9.如图所示,已知IS=3 A,US=90 V,R1=60Ω,R2=15Ω,RL=18Ω,则负载RL的电流为( )

A.1.8 A

B.1.6 A

C.1.4 A

D.1.2 A

10.关于电源间变换,下列叙述正确的是( )

A.理想电流源与理想电压源之间可以互换

B.电流源与电压源之间不能变换

C.电源间的变换对外电路是等效的

D.电源间的变换对内电路是等效的

二、填空题

1.实验测得某含源二端线性网络的开路电压为6 V,短路电流为2 A。当外接负载电阻为3Ω时,其端电压是_________V。

2.如图所示,已知通过R1的电流为3 A,则通过R2的电流为________A,通过R0的电流为_________A,电路的端电压为_________V。

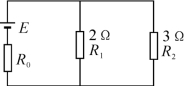
第2题图

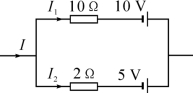
第3题图

3.如图所示,已知I=6 A,则I1=________A,I2=________A。

4.如图所示,已知US=6 V,IS=2 A,R=2Ω,则电阻中的电流I为_________A,电阻所消耗的电功率为________W。

第4题图

第5题图

5.如图所示,若回路的绕行方向为顺时针,则KVL方程为_____________,电阻R=_________Ω。

三、分析计算题

1.如图所示的电路中,已知E1=32 V,E2=11 V,R1=6Ω,R2=4Ω,R3=8Ω,求各支路电流I1、I2、I3。

第1题图

2.用戴维宁定理求1Ω电阻中的电流I。

第2题图

3.用叠加定理求4Ω电阻中的电流I。

第3题图